Abstände und Parallelität: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Repräsentantenunabhängigkeit) |
*m.g.* (Diskussion | Beiträge) (→Der Abstand zweier paralleler Geraden) |
||
| Zeile 4: | Zeile 4: | ||
Aus der Schule weiß man: | Aus der Schule weiß man: | ||
::Wenn <math>g \|| h</math>, dann hat <math>g</math> überall denselben Abstand zu <math>h</math>. | ::Wenn <math>g \|| h</math>, dann hat <math>g</math> überall denselben Abstand zu <math>h</math>. | ||
| − | In der Klausur | + | '''In der Klausur wird der Abstand zweier paralleler Geraden ein Rolle spielen.''' |
==Definition: Abstand zweier paralleler Geraden== | ==Definition: Abstand zweier paralleler Geraden== | ||
Version vom 6. Februar 2012, 10:40 Uhr
Inhaltsverzeichnis |
Vorbemerkung
Abstände spielen eine zentrale Rolle in der Geometrie. Logischerweise kann man die Klausur ohne Kenntnisse zu Abständen nicht bestehen.
Der Abstand zweier paralleler Geraden
Aus der Schule weiß man:
- Wenn
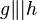, dann hat 
überall denselben Abstand zu 
.
- Wenn
In der Klausur wird der Abstand zweier paralleler Geraden ein Rolle spielen.
Definition: Abstand zweier paralleler Geraden
- Es seien und zwei nicht identische Geraden mit 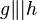. Ferner sei
ein beliebiger Punkt der Geraden . Der Anstand von zu ist der Abstand von zu .
- Es seien
- In Zeichen:
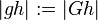
- In Zeichen:
Repräsentantenunabhängigkeit
Die obige Definition macht nur Sinn, Wenn gilt:
- Es seien und zwei Geraden mit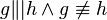
.
.
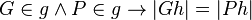- Es seien
Beweisen Sie diese Implikation.
Symmetrie
Beweisen Sie:
- Es seien und zwei Geraden mit .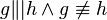
.
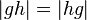- Es seien
