Übung Aufgaben 1 (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Aufgabe 1.3) |
HecklF (Diskussion | Beiträge) (→Aufgabe 1.2) |
||
| (7 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 19: | Zeile 19: | ||
# Jedes Quadrat ist ein Rechteck. | # Jedes Quadrat ist ein Rechteck. | ||
# Eine Raute ist ein Viereck mit vier gleich langen Seiten wobei je zwei Seiten parallel zueinander sind. | # Eine Raute ist ein Viereck mit vier gleich langen Seiten wobei je zwei Seiten parallel zueinander sind. | ||
| − | + | ||
[[Lösung von Aufgabe 1.1 (SoSe_12)]] | [[Lösung von Aufgabe 1.1 (SoSe_12)]] | ||
| Zeile 27: | Zeile 27: | ||
[[Lösung von Aufgabe 1.2 (SoSe_12)]] | [[Lösung von Aufgabe 1.2 (SoSe_12)]] | ||
| + | |||
| + | [[Lösung aus Übung Heckl 1.2 (SoSe_12)]] | ||
== Aufgabe 1.3== | == Aufgabe 1.3== | ||
| Zeile 33: | Zeile 35: | ||
* Sei <math>M</math> ein Punkt und <math>P</math> eine Menge, deren Elemente Punkte sind. Wenn gilt: <math>\left| MP \right|</math> ist konstant, so ist <math>P</math> ein Kreis mit Mittelpunkt <math>M</math>. | * Sei <math>M</math> ein Punkt und <math>P</math> eine Menge, deren Elemente Punkte sind. Wenn gilt: <math>\left| MP \right|</math> ist konstant, so ist <math>P</math> ein Kreis mit Mittelpunkt <math>M</math>. | ||
* Sei <math>M</math> ein Punkt und <math>P</math> eine Punktmenge. Wenn gilt: <math>X\in P:\left| XM \right|=r</math>, dann ist <math>P</math> ein Kreis. | * Sei <math>M</math> ein Punkt und <math>P</math> eine Punktmenge. Wenn gilt: <math>X\in P:\left| XM \right|=r</math>, dann ist <math>P</math> ein Kreis. | ||
| − | * Sei <math>M</math> ein Punkt in der Ebene <math>E</math> und <math>P</math> eine Punktmenge. Wenn <math>P</math> alle Punkte <math>X</math> enthält für die gilt∶ <math>\left| XM \right| | + | * Sei <math>M</math> ein Punkt in der Ebene <math>E</math> und <math>P</math> eine Punktmenge. Wenn <math>P</math> alle Punkte <math>X</math> enthält für die gilt∶ <math>\left| XM \right|=r,r\in \mathbb{R}^{+}</math> und <math>X\in E </math>, dann ist <math>P</math> ein Kreis mit dem Mittelpunkt <math>M</math>. |
| − | * Sei <math>M</math> ein Punkt in der Ebene <math>E</math> und <math>P</math> eine Menge, deren Elemente Punkte sind. Wenn für alle <math>X</math> | + | * Sei <math>M</math> ein Punkt in der Ebene <math>E</math> und <math>P</math> eine Menge, deren Elemente Punkte sind. Wenn für alle <math>X \in P</math> gilt∶ <math>\left| XM \right|=r,r\in \mathbb{R}^{+}</math>, dann ist <math>P</math> ein Kreis. |
* Sei <math>M</math> ein Punkt und <math>P</math> eine Menge, deren Elemente Punkte sind. Alle Elemente von <math>P</math> liegen in ein und derselben Ebene wie <math>M</math>. Wenn gilt: <math>\left| MP \right|</math> ist konstant, so ist <math>P</math> ein Kreis mit Mittelpunkt <math>M</math>. | * Sei <math>M</math> ein Punkt und <math>P</math> eine Menge, deren Elemente Punkte sind. Alle Elemente von <math>P</math> liegen in ein und derselben Ebene wie <math>M</math>. Wenn gilt: <math>\left| MP \right|</math> ist konstant, so ist <math>P</math> ein Kreis mit Mittelpunkt <math>M</math>. | ||
| Zeile 66: | Zeile 68: | ||
| − | [[ | + | [[Kategorie:Einführung_P]] |
| + | [[Kategorie:Einführung_S]] | ||
Aktuelle Version vom 25. April 2012, 16:32 Uhr
Inhaltsverzeichnis |
Aufgaben zu Definitionen
Aufgabe 1.1
Handelt es sich um Definitionen? Wenn ja, um welche Art von Definition (Real-, Konventional-, genetisch)? Begründen Sie!
- Jedes n-Eck mit n=4 heißt Viereck.
- Stufenwinkel an geschnittenen Parallelen sind kongruent.
- Eine Gerade heißt Dreiecksschneidende, falls es ein Dreieck gibt, dessen drei Seiten von der Geraden geschnitten werden, wobei die Eckpunkte des Dreiecks nicht zur Geraden gehören.
- Es gibt Vierecke mit einem Umkreis, die so genannten Sehnenvierecke.
- Wenn ein n-Eck vier Ecken hat, dann ist es ein Viereck.
- Es gibt Sehnenvierecke.
- Jeder Peripheriewinkel über einem Durchmesser ist ein Rechter.
- Ein rechter Winkel ist ein solcher, der zu einem seiner Nebenwinkel kongruent ist.
- Wenn ein Winkel zu einem seiner Nebenwinkel kongruent ist, so ist er ein Rechter.
- Ein Viereck, das so aussieht wie die Vierecke auf der bayrischen Fahne, heißt Raute.
- Es seien a und b zwei nichtidentische zueinander parallele Geraden. Lege auf a und b jeweils zwei verschiedene Punkte fest. Verbinde die vier Punkte zu einem konvexen Viereck. Du erhältst ein Trapez.
- Die Menge aller Punkte, die von den Endpunkten einer Strecke ein und denselben Abstand hat, heißt Mittelsenkrechte der Strecke.
- Eine Gerade, die senkrecht auf einer Strecke steht und diese halbiert, heißt Mittelsenkrechte der Strecke.
- Ein Rechteck hat vier rechte Innenwinkel.
- Jedes Quadrat ist ein Rechteck.
- Eine Raute ist ein Viereck mit vier gleich langen Seiten wobei je zwei Seiten parallel zueinander sind.
Lösung von Aufgabe 1.1 (SoSe_12)
Aufgabe 1.2
Definieren Sie die folgenden Begriffe mathematisch korrekt. Die Begriffe n-Eck, Seite und Ecke eines n-Ecks seien bereits definiert. Beziehen Sie sich auf den nächsthöheren Oberbegriff.
Viereck, Trapez, gleichschenkliges Trapez, Parallelogramm, Drachen, Raute, Rechteck, Quadrat
Lösung von Aufgabe 1.2 (SoSe_12)
Lösung aus Übung Heckl 1.2 (SoSe_12)
Aufgabe 1.3
Welche Definition für Kreis ist richtig? Warum (nicht)?
- Sei
ein Punkt und 
eine Menge, deren Elemente Punkte sind. Wenn gilt: 
ist konstant, so ist ein Kreis mit Mittelpunkt .
- Sei ein Punkt und eine Punktmenge. Wenn gilt: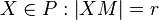
, dann ist ein Kreis.
- Sei ein Punkt in der Ebene
und eine Punktmenge. Wenn alle Punkte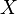 
enthält für die gilt∶ 
und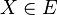 
, dann ist ein Kreis mit dem Mittelpunkt .
- Sei ein Punkt in der Ebene und eine Menge, deren Elemente Punkte sind. Wenn für alle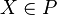
gilt∶ , dann ist ein Kreis.
- Sei ein Punkt und eine Menge, deren Elemente Punkte sind. Alle Elemente von liegen in ein und derselben Ebene wie . Wenn gilt: ist konstant, so ist ein Kreis mit Mittelpunkt .
Lösung von Aufgabe 1.3 (SoSe_12)
Aufgabe 1.4
Am 03. Febr. 2003 wurde in der Quiz-Sendung "Wer wird Millionär" folgende 16000 €-Frage gestellt:
Jedes Rechteck ist ein ...
Mit folgenden Auswahlantworten: Rhombus (Raute), Quadrat, Trapez, Parallelogramm
Nehmen Sie Stellung!
Lösung von Aufgabe 1.4 (SoSe_12)
Aufgabe 1.5
Kommentieren Sie den folgenden Definitionsversuch:
Definition: (gleichschenkliges Dreieck)
- Es gibt Dreiecke, die zwei zueinander kongruente Innenwinkel haben. Diese Dreiecke heißen gleichschenklige Dreiecke.
Lösung von Aufgabe 1.5 (SoSe_12)
Aufgabe 1.6
In welchen Fällen handelt es sich um eine korrekte Definition des Begriffs Parallelogramm? Begründen Sie!
- Wenn sich in einem Viereck die Diagonalen halbieren, so ist das Viereck ein Parallelogramm.
- Wenn in einem Drachen die gegenüberliegenden Seiten kongruent zueinander sind, so ist der Drachen ein Parallelogramm.
- Es gibt Trapeze, die ein weiteres Paar paralleler Seiten haben und die Parallelogramme genannt werden.
- Trapeze mit zwei zueinander kongruenten Seiten heißen Parallelogramme.
