Lösung von Aufgabe 7.3 S (SoSe 12): Unterschied zwischen den Versionen
| (11 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
<u>Widerlegung der Umkehrung durch eine Skizze:</u> [[Datei:RitterSport_Konvex.JPG]] | <u>Widerlegung der Umkehrung durch eine Skizze:</u> [[Datei:RitterSport_Konvex.JPG]] | ||
--[[Benutzer:RitterSport|RitterSport]] 19:52, 9. Jun. 2012 (CEST) | --[[Benutzer:RitterSport|RitterSport]] 19:52, 9. Jun. 2012 (CEST) | ||
| + | |||
| + | [[Datei:Geowiki 7.2..pdf]]--[[Benutzer:KeinKurpfälzer|KeinKurpfälzer]] 16:25, 11. Jun. 2012 (CEST) | ||
| + | |||
| + | [[Datei:Geo7.3..pdf]]--[[Benutzer:KeinKurpfälzer|KeinKurpfälzer]] 17:35, 11. Jun. 2012 (CEST)<br /> | ||
| + | Ich habe mir die eingescannten Beweise mal angeschaut, aber ich kann sie nur schlecht lesen und teilweise auch nicht nachvollziehen bzw. entziffern. Es wäre vllt. hilfreich, wenn man das ganze mit mehr Kontrast einscannen oder es noch einmal abtippen und ins Wiki stellen würde.--[[Benutzer:Andreas|Tutor Andreas]] 17:21, 1. Jul. 2012 (CEST) | ||
| + | |||
| + | |||
| + | == Lösungsvorschlag Nemo81 == | ||
| + | a) | ||
| + | |||
| + | Vor: 2 konvexe Punktmengen<br /> | ||
| + | 1. <math>\overline {AB}</math> ist echte Teilmenge von <math>M_1</math><br /> | ||
| + | 2. <math>\overline {AB}</math> ist echte Teilmenge von <math>M_2</math><br /> | ||
| + | |||
| + | |||
| + | Beh: Ihr Schnitt ist konvex <math>M_1</math> geschnitten <math>M_2</math> = konvex, d.h. <math>\overline {AB}</math> ist echte Teilmenge von <math>M_1</math> und <math>M_2</math> | ||
| + | |||
| + | |||
| + | Ann: Es existiert ein Punkt P: P <math>\in</math> <math>\overline {AB}</math> und P <math>\not\in M_2</math> . | ||
| + | |||
| + | Es kann solch einen Punkt nicht geben, weil laut Vor: Die <math>\overline {AB}</math> echte Teilmenge von <math>M_1</math> aber auch von <math>M_2</math> ist(und laut Def. konvex) | ||
| + | Also Widerspruch zur Vorraussetzung. q.e.d --[[Benutzer:Nemo81|Nemo81]] 17:57, 14. Jun. 2012 (CEST) | ||
| + | |||
| + | |||
| + | b)Wenn der Durchschnitt von zwei Punktmengen nicht konvex ist, dann sind die Punktmengen nicht konvex. | ||
| + | |||
| + | c)Wenn der Durchschnitt zweier Punktmengen konvex ist, dann sind die zwei Punktmengen auch konvex. | ||
| + | --[[Benutzer:Nemo81|Nemo81]] 18:15, 14. Jun. 2012 (CEST) | ||
Aktuelle Version vom 1. Juli 2012, 16:21 Uhr
Lösungsvorschlag:
Satz: Sind zwei Punktmengen konvex, dann ist auch ihr Durchschnitt konvex.
Beweis: ?
Kontraposition: Ist der Durchschnitt zweier Punktmengen nicht konvex, so sind die beiden Punktmengen auch nicht konvex.
Umkehrung des Satzes: Ist der Durchschnitt zweier Punktmengen konvex, dann sind die beiden Punktmengen konvex.
Widerlegung der Umkehrung durch eine Skizze: 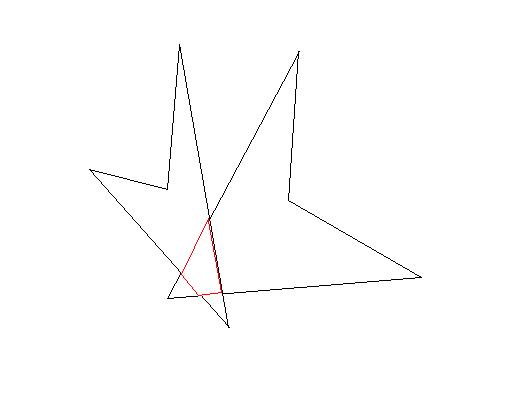
 --KeinKurpfälzer 16:25, 11. Jun. 2012 (CEST)
--KeinKurpfälzer 16:25, 11. Jun. 2012 (CEST)
 --KeinKurpfälzer 17:35, 11. Jun. 2012 (CEST)
--KeinKurpfälzer 17:35, 11. Jun. 2012 (CEST)
Ich habe mir die eingescannten Beweise mal angeschaut, aber ich kann sie nur schlecht lesen und teilweise auch nicht nachvollziehen bzw. entziffern. Es wäre vllt. hilfreich, wenn man das ganze mit mehr Kontrast einscannen oder es noch einmal abtippen und ins Wiki stellen würde.--Tutor Andreas 17:21, 1. Jul. 2012 (CEST)
Lösungsvorschlag Nemo81
a)
Vor: 2 konvexe Punktmengen
1.  ist echte Teilmenge von
ist echte Teilmenge von 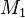
2.  ist echte Teilmenge von
ist echte Teilmenge von 
Beh: Ihr Schnitt ist konvex 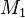 geschnitten
geschnitten  = konvex, d.h.
= konvex, d.h.  ist echte Teilmenge von
ist echte Teilmenge von  und
und 
Ann: Es existiert ein Punkt P: P 
 und P
und P 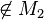 .
.
Es kann solch einen Punkt nicht geben, weil laut Vor: Die  echte Teilmenge von
echte Teilmenge von 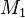 aber auch von
aber auch von  ist(und laut Def. konvex)
Also Widerspruch zur Vorraussetzung. q.e.d --Nemo81 17:57, 14. Jun. 2012 (CEST)
ist(und laut Def. konvex)
Also Widerspruch zur Vorraussetzung. q.e.d --Nemo81 17:57, 14. Jun. 2012 (CEST)
b)Wenn der Durchschnitt von zwei Punktmengen nicht konvex ist, dann sind die Punktmengen nicht konvex.
c)Wenn der Durchschnitt zweier Punktmengen konvex ist, dann sind die zwei Punktmengen auch konvex. --Nemo81 18:15, 14. Jun. 2012 (CEST)

