Beziehungen zwischen den Seitenlängen und den Innenwinkelgrößen eines Dreiecks WS 11/12
Inhaltsverzeichnis |
Satz IX.2: (Der größeren Seite liegt der größere Winkel gegenüber)
- Es sei
 ein Dreieck mit den schulüblichen Bezeichnungen.
ein Dreieck mit den schulüblichen Bezeichnungen.
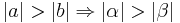
- Es sei
Beweis von Satz IX.2
Es sei  ein Dreieck.
ein Dreieck.
Voraussetzung:
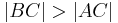 bzw.
bzw. 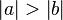
Behauptung:
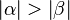
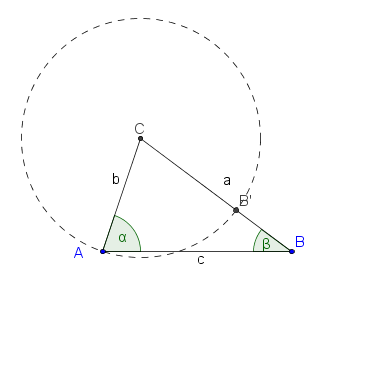
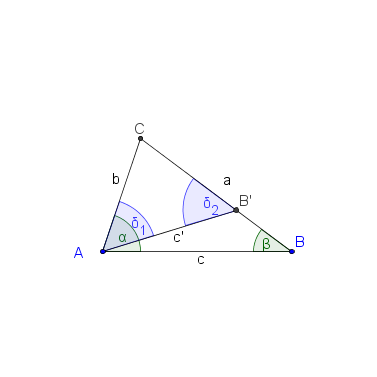
Die folgenden Hilfskonstruktionen liefern die Beweisidee (kommentieren Sie die Abbildungen und führen Sie den Beweis):
Satz IX.3: (Dem größeren Winkel liegt die größere Seite gegenüber)
- Es sei
 ein Dreieck mit den schulüblichen Bezeichnungen.
ein Dreieck mit den schulüblichen Bezeichnungen. 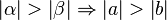
- Es sei
Beweis von Satz IX.3
Übungsaufgabe
"Bierkastenbeweis"
Ich denke ich kann beweisen wie in der Vorlesung heute Morgen gewünscht.
Weiß nur nicht ob ich diesen Beweis in Wiki stellen soll, möchte es unseren Nachfolgern auch wieder die Chance lassen einen Kasten zu gewinnen.
Was meint ihr?--RicRic 16:58, 20. Jan. 2012 (CET)
Nachdem ich ja jetzt den Bierkasten habe, möchte ich bei erhalt jeden der sich dises Semester öfters akiv im Geowiki beteiligt hat, auf ein Bier einladen, die Tutoren natürlich auch und nur solange der Vorrat reicht :-)--RicRic 16:47, 28. Jan. 2012 (CET)
Vor: 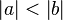
Beh.: 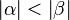
Beweis:
| Überschrift 1 | Überschrift 2 |
|---|---|
(1) 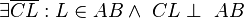 |
Existenz und Eindeutigkeit des Lotes von einem Punkt auf eine Gerade |
(2) 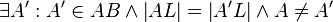 |
Axiome Abstand, Lineal, (1) |
(3) 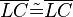 |
trivial |
(4) 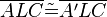 |
SWS, (1),(2),(3) |
(5) 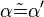 |
(4) |
(6) 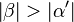 |
schwacher Ausenwikelsatz |
(7) 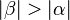 |
(5),(6) |
Die Überlegung, Falls A' zwischen L und B liegen sollte, konnte ich magels Zeit leider nicht mehr vorstellen.
| Überschrift 1 | Überschrift 2 |
|---|---|
(1) 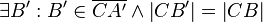 |
Axiom Lineal und Abstand |
(2) 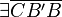 ist Gelichschenklig ist Gelichschenklig |
(1) |
(3) 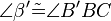 |
Basiswikelsatz (2) |
(4) 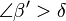 |
schwacher Ausenwikelsatz |
(5) 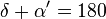 |
nebenwinkel sind sulimentär |
| Wiederspruch ( 3),(4),(5) in einem Dreieck sie Summer zweier Innenwinkel immer kleiner als 180 sein muss Kollar zum schw Außenwineklsatz. Somit kann A nicht zwischen L und B liegen. |
--RicRic 17:39, 28. Jan. 2012 (CET)
zweite Idee:
Vor: 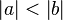
Beh.: 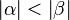
Beweis:
| Überschrift 1 | Überschrift 2 |
|---|---|
(1) 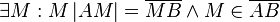 |
Existenz und Eindeutigkeit des Mittelpunks einer Strecke |
(2) 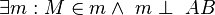 |
Existenz und Eindeutigkeit der Mittelsenkrechten einer Stecke, (1) |
(3) Fall 1: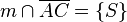 |
Axiom von Pasch, Vor,2 |
(4) 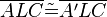 |
SWS, (1),(2),(3) |
(5) 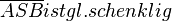 |
(3) Mittelsenkrechtenkriterum |
(6) 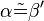 |
(4) Basiswinkelsatz |
(7) 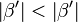 |
S im inneren von beta (4) Lemma, wenn die Endpunte einer Strecke auf den Schenkeln eines Winkels liegen liegt die gesamte Strecke im inneren des Winkels; Lemma, wenn ein Punkt im inneren eins Winkels liegt, liegt der gesamte Strahl im innenern dieses Winkels |
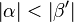 |
(5),(6) |
Fall2: m schneidet den Punkt C, daraus folgt nach dem Mitttelsenkrechtenkriterium, dass 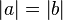
Wiederspruch zur Vorr.
Fall3: m schneidet die Strecke 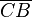 darus folgt, A und C sind bezüglich m in der gleichen Halbebene, da eine Halbebene eine konvexe Punktmenge ist und M der Mittelpunkt von
darus folgt, A und C sind bezüglich m in der gleichen Halbebene, da eine Halbebene eine konvexe Punktmenge ist und M der Mittelpunkt von  und M der Mittelsenktrechten angehöt, müsste dies bedeuten:
und M der Mittelsenktrechten angehöt, müsste dies bedeuten: 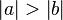
und ist somit ein Wiederspruch zur Vorr.--RicRic 17:04, 28. Jan. 2012 (CET)
Beweisidee:
Ich weiß nicht, obs zu simple wäre, aber Herr Schnirch meinte, 2 Zeilen reichen.
Vor.:
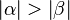
Beh.:
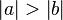
Annahme:
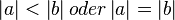 oBdA
oBdA
Beweis Fall 1:
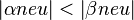 Begründung: Annahme, Satz IX.2 (größere Seite, größerer Winkel)
Begründung: Annahme, Satz IX.2 (größere Seite, größerer Winkel)
Widerspruch zur Vor.
Beweis Fall 2:
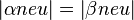 Begründung: Annahme, Basiswinkelsatz
Begründung: Annahme, Basiswinkelsatz
Widerspruch zur Vor.
ps
Ja halte ich für richtig.--RicRic 07:55, 23. Jan. 2012 (CET)