Bin ich fit für die Klausur: das gleichschenklige Trapez WS 12 13: Unterschied zwischen den Versionen
Yellow (Diskussion | Beiträge) (→Definition 2, ergänzen) |
(→Definition 1, der Klassiker) |
||
| Zeile 61: | Zeile 61: | ||
====Symmetrische Trapeze und gleichschenklige Trapeze==== | ====Symmetrische Trapeze und gleichschenklige Trapeze==== | ||
Die Begriffe ''symmetrisches Trapez'' und ''gleichschenkliges Trapez'' sind synonym. Also jedes gleichschenklige Trapez ist ein symmetrisches Trapez und umgekehrt. Wie an anderen Stellen ausgeführt können wir den Begriff der Symmetrie nicht explizit verwenden, da wir ihn nicht definieren im Rahmen der Einführung in die Geometrie. Wir behelfen uns mit speziellen Mittelsenkrechteneigenschaften. Das passt aber nicht in diesen Abschnitt. In diesem Abschnitt zur Definition gleichschenkligen Trapeze verwenden wir die Semantik des Namens gleichschenkliges Trapez und nicht die Semantik des Namens symmetrisches Trapez. | Die Begriffe ''symmetrisches Trapez'' und ''gleichschenkliges Trapez'' sind synonym. Also jedes gleichschenklige Trapez ist ein symmetrisches Trapez und umgekehrt. Wie an anderen Stellen ausgeführt können wir den Begriff der Symmetrie nicht explizit verwenden, da wir ihn nicht definieren im Rahmen der Einführung in die Geometrie. Wir behelfen uns mit speziellen Mittelsenkrechteneigenschaften. Das passt aber nicht in diesen Abschnitt. In diesem Abschnitt zur Definition gleichschenkligen Trapeze verwenden wir die Semantik des Namens gleichschenkliges Trapez und nicht die Semantik des Namens symmetrisches Trapez. | ||
| + | |||
| + | Definition: (Trapez, zwei Seiten kongruent) | ||
| + | Ein Trapez nennt man gleichschenklig, wenn es ein Paar zueinander kongruente, jedoch nicht parallele, Seiten hat, oder ein Rechteck ist. --[[Benutzer:...lw)...|...lw)...]] 09:17, 5. Feb. 2013 (CET) | ||
==Definition 2== | ==Definition 2== | ||
Version vom 5. Februar 2013, 10:17 Uhr
Vorbemerkung
In der Datei Klausurvorbereitung_WS_12_13:_Lisa_reloaded_oder_der_Heidelberger_Viereckskreis haben Sie richtig erkannt, dass es in der Klausur wohl u.a. um gleichschenklige bzw. symmetrische Trapeze gehen wird.
Sie sollten die Zeit nutzen und sich intensiv mit dem Begriff auseinandersetzen.
Das gleichschenklige Trapez entsprechen der Semantik des Namens
Der Begriff wird mittels der Eigenschaft Trapez zu sein und die gleichlangen Seiten definiert. Sie sollten in der Lage sein 5 verschiedene Definition diesbezüglich zu entwickeln:
Definition 1, der Klassiker
Trapez, zwei Seiten kongruent
Definition
gleichschenkliges Trapez
Ein Trapez, das zwei kongruente gegenüberliegende Seiten hat, ist dann ein gleichschenkliges Trapez, wenn diese beiden Seiten entweder nicht parallel sind oder das Trapez ein Rechteck ist--LilPonsho 16:08, 31. Jan. 2013 (CET) ....
Ein Trapez ist ein gleichschenkliges Trapez, wenn es zwei kongruente Seiten hat. (Dabei wäre auch ein Parallelogramm ein gleichschenkliges Trapez) --Yellow 22:24, 27. Jan. 2013 (CET)
@ Yellow:
Das ist ganz richtig.
Wichtig ist eventuell zu zeigen, dass nicht jedes gleichschenklige Trapez auch ein symmetrisches Trapez ist.--Sweetnightmare5 13:55, 28. Jan. 2013 (CET)
was ist denn der Unterschied zwischen einem gleichschenkligen und einem symmetrischen Trapez ? (Sallyfield)
Ein gleichschenkliges Trapez kann auch ein Parallelogramm sein. Aber nicht jedes Parallelogramm ist symmetrisch. --Sweetnightmare5 18:30, 28. Jan. 2013 (CET)
ähhhhmm...
- Nur spezielle Parallelogramme sind gleichschenklige Trapeze! nämlich Rechtecke. Deshalb muss man doch beim Definieren des
gl. Trapezes das Parallelogramm ausschließen, aber Rechtecke als Spezialfall des Parallelogramms muss mit dabei sein?!oder?
So haben wir das auch verstanden, wir können doch eigentlich immer das Parallelogramm ausschließen und können von einem Rechteck reden? (Sallyfield)
Ein Trapez ist somit ein gleichschenkliges Trapez, wenn es zwei kongruente Seiten hat, die nicht parallel sind außer das Trapez wäre ein Rechteck.
Aber was wäre dann der Unterschied dieser Definition zur zweiten Definition? (Sallyfield)
@sallyfield: ja das hat mich auch erst gewundert, aber jetzt hat Herr Gieding ja was dazugeschrieben weiter unten, dass wir hier bei 1 mit parallel/ bzw. nicht parallel definieren sollen, und bei 2 dann explizit den Begriff des Parallelogramms benutzen sollen. Ich stimme deiner Definition zu! vll muss aber noch das gegenüberliegend rein und ein entweder-oder: Ein Trapez, das zwei kongruente gegenüberliegende Seiten hat, ist dann ein gleichschenkliges Trapez, wenn diese beiden Seiten entweder nicht parallel sind oder das Trapez ein Rechteck ist.--LilPonsho 20:28, 30. Jan. 2013 (CET)
- was ist der Unterschied zwischen gl. Trapez und einem symetrischen Trapez???--LilPonsho 20:02, 28. Jan. 2013 (CET)
Entschuldigt bitte meine Verwirrung, ich bin bis gerade davon ausgegangen, dass ein Parallelogramm automatisch auch ein gleichschenkliges Trapez ist, und bin mir auch immer noch nicht ganz sicher ob es nicht doch der Fall ist.
Könnte man denn nicht sagen: Ein Trapez ist dann ein gleichschenkliges, wenn es ein paar kongruenter Seiten hat und ein paar nicht paralleler Seiten oder einen Rechten Innenwinkel hat. Damit wäre das Parallelogramm weitestgehend (bis auf das Rechteck) ausgenommen.--Sweetnightmare5 14:49, 29. Jan. 2013 (CET)
Bemerkungen --*m.g.* 10:07, 30. Jan. 2013 (CET)
Parallelogramme und gleichschenklige Trapeze
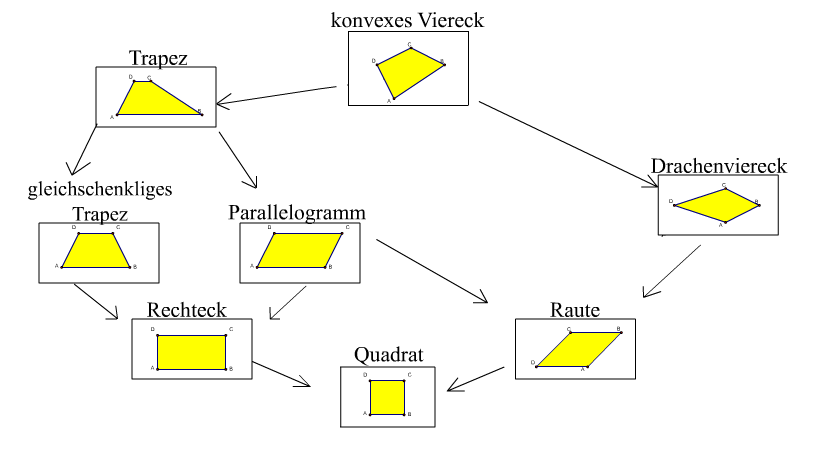
Schauen Sie sich das Haus der Vierecke noch einmal an: Vom Trapez gehen zwei gleichberechtigte Pfeile aus: Parallogramme als ein Spezialfall der Trapeze und gleichschenklige Trapeze als ein zweiter Spezialfall der Trapeze. Beide Teilmengen Parallelogramme als auch gleichschenklige Trapeze befinden sich auf derselben Hierarchiestufe im Haus der Vierecke. Unterhalb dieser Hierarchiestufe wird wieder zusammengeführt: Die Rechtecke sind sowohl Parallelogramme als auch gleichschenklige Trapeze:
Damit ist ein gleichschenkliges Trapez dann und nur dann ein Parallelogramm, wenn es ein Rechteck ist.
Trapez, zwei Seiten kongruent
Definition
gleichschenkliges Trapez
Ein Trapez ist gleichschenklig, wenn es entweder ein Rechteck ist oder zwei gegenüberliegende Seiten hat, die
kongruent zueinander sind und nicht parallel (Sallyfield) ...
Definition
<Ein Trapez, das zwei kongruente gegenüberliegende Seiten hat, ist dann ein gleichschenkliges Trapez, wenn diese beiden Seiten entweder nicht parallel sind oder das Trapez ein Rechteck ist. (LilPonsho)>
Hier mal mein Versuch: Ein Trapez ist genau dann gleichschenklich, wenn die Diagonalen gleich lang sind. (Waynetrain)'
@waynetrain: richtige Definition, nur hast du nicht die vorgegebenen Eigenschaften benutzt!--LilPonsho 20:54, 30. Jan. 2013 (CET)
Geht das: Ein trapez mit zwei sich gegenüberliegenden kongruenten Seiten heißt gleichschenkliges Trapez, wenn es kein Parallelogramist , es sei denn, es ist ein Rechteck? beta91
@beta91: ja geht! nur gehört diese Definition zu Definition 2!!! siehe Kommentar von Herr Gieding weiter unten bei Intention...:"Definition 1 verwendet nicht explizit den Begriff Parallelogramm. Wir verwenden stattdessen den Begriff parallel bzw. nicht parallel. In Definition 2 wollen wir explizit den Begriff Parallelogramm verwenden. "--LilPonsho 16:03, 31. Jan. 2013 (CET)
Symmetrische Trapeze und gleichschenklige Trapeze
Die Begriffe symmetrisches Trapez und gleichschenkliges Trapez sind synonym. Also jedes gleichschenklige Trapez ist ein symmetrisches Trapez und umgekehrt. Wie an anderen Stellen ausgeführt können wir den Begriff der Symmetrie nicht explizit verwenden, da wir ihn nicht definieren im Rahmen der Einführung in die Geometrie. Wir behelfen uns mit speziellen Mittelsenkrechteneigenschaften. Das passt aber nicht in diesen Abschnitt. In diesem Abschnitt zur Definition gleichschenkligen Trapeze verwenden wir die Semantik des Namens gleichschenkliges Trapez und nicht die Semantik des Namens symmetrisches Trapez.
Definition: (Trapez, zwei Seiten kongruent) Ein Trapez nennt man gleichschenklig, wenn es ein Paar zueinander kongruente, jedoch nicht parallele, Seiten hat, oder ein Rechteck ist. --...lw)... 09:17, 5. Feb. 2013 (CET)
Definition 2
Trapez mit gleichlangen Seiten, kein Parallelogram, es sei denn ...
Definition
gleichschenkliges Trapez
Ein Trapez mit zwei gleichlangen gegenüberliegenden Seiten, das kein Parallelogramm ist, es sei denn es besitzt einen rechten Innenwinkel, heißt gleichschenkliges Trapez --LilPonsho 21:18, 30. Jan. 2013 (CET)
Ein Trapez mit zwei gleichlangen gegenüberliegenden Seiten, das kein Parallelogramm ist, es sei denn es es ist ein Rechteck, heißt gleichschenkliges Trapez --LilPonsho 21:18, 30. Jan. 2013 (CET)....
Ein Trapez ist ein gleichschenkliges Trapez, wenn es zwei kongruente Seiten hat, die nicht parallel sind außer Trapez wäre ein Rechteck.
--Yellow 22:26, 27. Jan. 2013 (CET)
Ein Trapez, das zwei kongruente gegenüberliegende Seiten hat, ist dann ein gleichschenkliges Trapez, wenn diese beiden Seiten entweder nicht parallel sind oder das Trapez ein Rechteck ist.
(Sallyfield) find ich gut--LilPonsho 20:07, 28. Jan. 2013 (CET)
Anmerkung zu den oberen Definitionen: Ein Parallelogramm ist IMMER ein Trapez, nicht nur wenn es ein Rechteck ist.--Sweetnightmare5 14:53, 29. Jan. 2013 (CET)
Ein Parallelogramm ist immer ein Trapez aber nie ein gleichschenkliges Trapez, es sei denn es sei ein spezielles Parallelogramm, nämlich ein Rechteck. (Sallyfield)
Meine Definition: Ein Trapez ist dann ein gleichschenkliges, wenn es ein Paar gleich langer Seiten hat. Es ist kein Parallelogramm, es sei denn es hat zwei Paar kongruenter Seiten.--Sweetnightmare5 13:14, 28. Jan. 2013 (CET)
Bemerkungen --*m.g.* 10:32, 30. Jan. 2013 (CET)
Intention des Unterschiedes zu Definition 1
Definition 1 verwendet nicht explizit den Begriff Parallelogramm. Wir verwenden stattdessen den Begriff parallel bzw. nicht parallel. In Definition 2 wollen wir explizit den Begriff Parallelogramm verwenden.
Bewertung der formulierten Definitionen
Yellow
Ein Trapez ist ein gleichschenkliges Trapez, wenn es zwei kongruente Seiten hat, die nicht parallel sind außer Trapez wäre ein Rechteck. --Yellow 22:26, 27. Jan. 2013 (CET) Vorab: Es fehlt der Artikel vor dem dritten Trapez (... außer Trapez wäre ein Rechteck..., feiner Deutsch) Konzentration!
Was wäre mit dem hier? Nach Ihrer Definition wäre es ein gleichschenkliges Trapez.
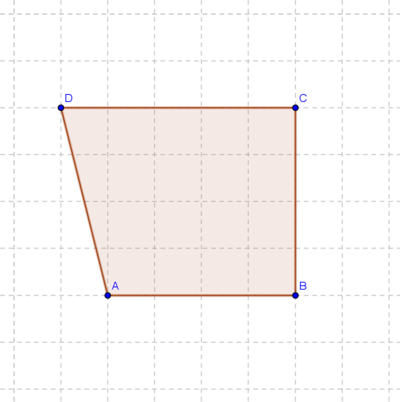
- hat zwei zueinander parallele Seiten bzw. ist ein Trapez
- hat zwei Seiten, die kongruent und nicht parallel sind (
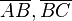 )
)
- ist trotzdem kein gleichschenkliges Trapez
Du hast vergessen zu sagen, dass es zwei gegenüberliegenden kongruenten Seiten hat. Dann ist der Fall auf dem Bild nämlich ausgeschlossen (Sallyfield)
Ein Trapez ist gleichschenklig, wenn es zwei gegenüberliegende gleichlange Seiten hat, die nicht parallel sind. Demnach ist das Trapez kein Parallelogramm, es sei denn das Trapez ist ein Rechteck. (Sallyfield)
Definition 3
als Oberbegriff wird diesmal Viereck verwendet, sonst wie Definition 1
Definition
gleichschenkliges Trapez
Ein Viereck, bei dem ein Seitenpaar parallel und das andere sich gegenüberliegende Seitenpaar kongruent zueinander ist, ist dann ein gleichschenkliges Trapez, wenn das kongruente Seitenpaar entweder nicht parallel ist oder das Viereck ein Rechteck ist--LilPonsho 22:12, 30. Jan. 2013 (CET) ....
Ein Viereck ist ein gleichschenkliges Trapez, wenn ein Seitenpaar parallel ist und das andere Paar Seiten kongruent zueinander ist. --Yellow 22:29, 27. Jan. 2013 (CET)
Anmerkung: Es können auch beide Eigenschaften, also Kongruenz und Parallelität für das selbe "Seitenpaar" zutreffen. Dann ist es übrigens ein Parallelogramm.
Für mich ergibt sich somit eine andere Definition: Ein Viereck, das ein Paar paralleler und zwei kongruente Seiten hat, ist ein gleichschenkliges Trapez. --Sweetnightmare5 13:21, 28. Jan. 2013 (CET)
puhhh für mich sagen beide Definitionen iwie das Gleiche aus! es soll genau ein Seitenpaar parallel sein und das andere Seitenpaar kongruent zueinander, damit es ein gleichschenkliges Trapez ist... aber beide Definitionen können doch Parallelogramme sein, und wenn man es mit "genau einem parallen Seitenpaar" definieren würde, dann wäre das Rechteck ausgeschlossen, kann also auch nicht sein!!
Es muss in die Richtung gehen:
Ein Viereck, bei dem ein Paar von Seiten parallel zueinander ist und die nicht parallelen Seiten kongruent sind oder es ein Rechteck ist, heißt gleichschenkliges Trapez.--LilPonsho 20:29, 28. Jan. 2013 (CET)
Okay, dann auch von mir ein neuer Versuch:
Ein Viereck ist ein gleichschenkliges Trapez, wenn es ein Paar paralleler und ein Paar kongruenter Seiten hat. Zudem ist ein Seitanpaar nicht parallel, es sei denn es ist ein Rechteck.--Sweetnightmare5 15:01, 29. Jan. 2013 (CET)
Wenn ein Viereck ein Rechteck ist oder wenn es ein Paar gegenüberliegende parallele Seiten hat und die anderen Seiten kongruent zueinander sind, dann ist das Viereck ein gleichschenkliges Trapez (Sallyfield)
@ Sallyfield: Musst du in deiner Definition jetzt nicht noch ausschließen, dass das Viereck ein Parallelogramm ist, indem du sagst, dass die beiden zueinander kongruenten Seiten nicht parallel zueinander sind? --Caro44 14:28, 30. Jan. 2013 (CET) @sallyfield & @caro44: ja genau is mir auch grad aufgefallen! caro44 hat sinngemäß Recht--LilPonsho 21:27, 30. Jan. 2013 (CET)
Definition 4
als Oberbegriff wird diesmal Viereck verwendet, sonst wie Definition 2
Definition
gleichschenkliges Trapez
Ein Viereck, mit zwei parallelen und zwei gegenüberliegenden gleichlangen Seiten, das kein Parallelogramm ist, es sei denn es beitzt einen rechten Innenwinkel, heißt gleichschenkliges Trapez.
Ein Viereck, mit zwei parallelen und zwei gegenüberliegenden gleichlangen Seiten, das kein Parallelogramm ist, es sei denn es ist ein Rechteck, heißt gleichschenkliges Trapez.--LilPonsho 22:21, 30. Jan. 2013 (CET)....
Ein Viereck ist ein gleichschenkliges Trapez, wenn ein Seitenpaar parallel ist und das andere Paar Seiten kongruent zueinander ist, jedoch nicht Parallel außer das Viereck ist ein Rechteck. --Yellow 22:31, 27. Jan. 2013 (CET)
Wenn ein Viereck ein Rechteck ist oder wenn ein paar Seiten parallel sind und das andere Paar kongruent, dann ist das Viereck ein gleichschenkliges Trapez.
(Sallyfield)
Wenn ein Viereck ein paar gegenüberliegende parallele Seiten hat und die anderen Seiten gleich lang sind, aber nicht parallel, dann ist das Viereck ein gleichschenkliges Trapez und kein Parallelogramm, es sei denn es ist ein Rechteck. (Sallyfield)
@sally: iwie doppelt gemobbelt: " nicht parallel" - kein Parallelogramm, --> es muss rein würd ich sagen : Viereck, ein Seitenpaar parallel, das andere sich gegenüberliegende Seitenpaar gleich lang, das kein Parallogramm ist, es sein denn es ist ein Rechteck, heißt gl. Trapez siehe Definition oben (LilPonsho)
Definition 5
das Ganze mal als operational genetische Definition
Definition
gleichschenkliges Trapez
Es seien  und
und  zwei zueinander parallele Geraden. Wenn man auf
zwei zueinander parallele Geraden. Wenn man auf  die Punkte
die Punkte  und
und  und auf
und auf  die Punkte
die Punkte  und
und  derart wählt, dass ....
derart wählt, dass ....
... gilt 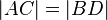 , so erhält man ein gleichschenkliges Trapez. --Sweetnightmare5 13:34, 28. Jan. 2013 (CET)
, so erhält man ein gleichschenkliges Trapez. --Sweetnightmare5 13:34, 28. Jan. 2013 (CET)
Du meintest doch sicherlich 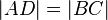 oder wolltest du über die Diagonalen, dann müsstest du nämlich noch dazu sagen, dass sich AC und BD im selben Verhältnis schneiden?
oder wolltest du über die Diagonalen, dann müsstest du nämlich noch dazu sagen, dass sich AC und BD im selben Verhältnis schneiden?
Kommt drauf an wie man die Punkte wählt... wenn du in deiner Skizze der Punkte die Buchstaben C und D vertauschst, sind nicht mehr die Diagonalen entscheidend.... Wenn ich in meiner Definition die Diagonalen gemeint hätte, wäre diese nicht korrekt. PS: Bitte schreibe zu deinem Kommentar noch deine Signatur...--Sweetnightmare5 13:11, 29. Jan. 2013 (CET)
Wenn man auf  die Punkte
die Punkte  und
und  und auf
und auf  die Punkte
die Punkte  und
und  derart wählt, dass die Strecke
derart wählt, dass die Strecke 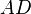 kongruent zur Strecke
kongruent zur Strecke 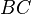 ist und entweder die Strecke
ist und entweder die Strecke  größer als die Strecke
größer als die Strecke 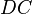 ist oder umgekehrt, dann ist ABCD ein gleichschenkliges Trapez. --Caro44 14:37, 30. Jan. 2013 (CET)
ist oder umgekehrt, dann ist ABCD ein gleichschenkliges Trapez. --Caro44 14:37, 30. Jan. 2013 (CET)
@caro44: ich find deine definition gut, dachte auch erst sie is korrekt so, aber was ich mich jetzt frage, ist folgendes: dadurch das du schreibst "und entweder die Strecke  größer als die Strecke
größer als die Strecke 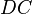 ist oder umgekehrt" kann ja nie ein Rechteck entstehen... mir ist klar, dass du es so formuliert hast um das Parallelogramm auszuschließen, aber es fehlen so halt Rechteck und somit auch das Quadrat, die ja bei der Definition des gleichschenkligen Trapezes nicht ausgeschlossen werden dürfen.--LilPonsho 22:41, 30. Jan. 2013 (CET)
ist oder umgekehrt" kann ja nie ein Rechteck entstehen... mir ist klar, dass du es so formuliert hast um das Parallelogramm auszuschließen, aber es fehlen so halt Rechteck und somit auch das Quadrat, die ja bei der Definition des gleichschenkligen Trapezes nicht ausgeschlossen werden dürfen.--LilPonsho 22:41, 30. Jan. 2013 (CET)
Idee:
Wenn man auf  die Punkte
die Punkte  und
und  und auf
und auf  die Punkte
die Punkte  und
und  derart wählt, dass die Strecke
derart wählt, dass die Strecke 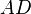 kongruent zur Strecke
kongruent zur Strecke 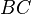 ist, ist entweder eine der Strecken
ist, ist entweder eine der Strecken  bzw.
bzw. 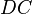 größer als die andere, oder Strecke
größer als die andere, oder Strecke 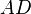 und
und 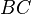 ist Lot sodass
ist Lot sodass  =
= 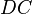 ist , dann ist ABCD ein gleichschenkliges Trapez.--LilPonsho 22:58, 30. Jan. 2013 (CET)
ist , dann ist ABCD ein gleichschenkliges Trapez.--LilPonsho 22:58, 30. Jan. 2013 (CET)
oder "einfach" so:
Wenn man auf  die Punkte
die Punkte  und
und  und auf
und auf  die Punkte
die Punkte  und
und  derart wählt, dass die Strecke
derart wählt, dass die Strecke 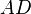 kongruent zur Strecke
kongruent zur Strecke 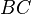 ist, ist eine der Strecken
ist, ist eine der Strecken  bzw.
bzw. 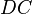 größer als die andere,es sei denn es ist ein Rechteck,dann ist ABCD ein gleichschenkliges Trapez.--LilPonsho 16:28, 31. Jan. 2013 (CET)
größer als die andere,es sei denn es ist ein Rechteck,dann ist ABCD ein gleichschenkliges Trapez.--LilPonsho 16:28, 31. Jan. 2013 (CET)
@LilPonsho: Danke für deinen Hinweis! Ich war zu sehr damit beschäftigt das Parallelogramm auszuschließen und habe dabei vergessen, dass das gleichschenkl. Trapez ja auch ein Rechteck sein kann. Deine Definition ist meiner Meinung nach richtig! ;-)--Caro44 15:10, 3. Feb. 2013 (CET)
Das gleichschenklige Trapez als abgeschnittenes gleichschenkliges Dreieck
Definition 1, abschneiden
Definition
gleichschenkliges Trapez
Es sei  ein gleichschenkliges Dreieck mit der Basis
ein gleichschenkliges Dreieck mit der Basis  . Ferner sei
. Ferner sei  eine Gerade, die ...
eine Gerade, die ...
...die parallel zu der Basis ist und die Schenkel des Dreiecks in den Punkten  und
und  schneidet. Das Viereck
schneidet. Das Viereck 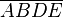 ist ein gleichschenkliges Trapez.--Sweetnightmare5 13:41, 28. Jan. 2013 (CET)
ist ein gleichschenkliges Trapez.--Sweetnightmare5 13:41, 28. Jan. 2013 (CET)
Definition 2, ergänzen
Definition
gleichschenkliges Trapez
Es sei  ein Trapez mit
ein Trapez mit 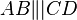 .
.  ist gleichschenklig, wenn das Dreieck ....
ist gleichschenklig, wenn das Dreieck ....
ein gleichschenkliges Dreieck ist und ein Schenkel parellel zur Seite DA ist und Punkt C des Dreiecks identisch mit Punkt C des Trapezes ist.
--Yellow 22:38, 27. Jan. 2013 (CET)
... 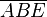 gleichschenklig ist, und die Schenkel des Trapezes
gleichschenklig ist, und die Schenkel des Trapezes 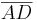 und
und  Teilmengen der Schenkel des Dreiecks
Teilmengen der Schenkel des Dreiecks 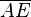 und
und 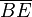 sind.--Sweetnightmare5 09:57, 29. Jan. 2013 (CET)
sind.--Sweetnightmare5 09:57, 29. Jan. 2013 (CET)
Dürfen wir bei einem gleichschenkligen Trapez überhaupt von Schenkeln reden? Das wurde doch so nie definiert ? (Sallyfield)
Naja, wenn du von gleich-schenklig sprichst, dass darf man doch das Wort Schenkel verwenden...
Ansonsten müsste man wirklich noch Basis eines Trapezes und die daran anliegenden Schenkel Definieren. Ich habe das jetz nur mal vom Dreieck abgeleitet. Außerdem könnte man, wenn man es ernst nimmt bei einem Trapez auch von Seiten reden.--Sweetnightmare5 15:46, 29. Jan. 2013 (CET)
@Sweetnightmare5: wie passt in deine Definition der Sonderfall Rechteck rein? Vielleicht passt diese Definition: gleichschenklig ist und, die Mittelsenkrechte des Dreiecks identisch ist mit der Mittelsenkrechter der längeren parallelen Seite des Trapezes.
--Yellow 21:29, 4. Feb. 2013 (CET)
Das gleichschenklige Trapez als symmetrisches Trapez bzw. als Sehnenviereck
Bringen Se hier entsprechende Definitionen unter. Wir haben und werden Symmetrie nicht definieren, sie können nur über Eigenschaften der Mittelsenkrechten definieren.
Natürliches Mineralwasser
1. Ein Trapez, das zwei kongruente gegenüberliegende Seiten hat, ist dann ein gleichschenkliges Trapez, wenn diese beiden Seiten entweder nicht parallel sind oder das Trapez ein Rechteck ist.
2. Ein Trapez, das achsensymmetrisch ist und das eine Symmetrieachse hat, die verschieden von den Diagonalen des Trapezes ist, heißt gleichschenkliges Trapez.
3. Ein Trapez mit einem Umkreis heißt gleichschenkliges Trapez.
4. Ein Trapez, in dem nicht gegenüberliegende Innenwinkel zu einander kongruent sind, heißt gleichschenkliges Trapez.
--Natürliches Mineralwasser 18:05, 3. Feb. 2013 (CET)
--*m.g.* 19:08, 3. Feb. 2013 (CET)
zu 2.
- Vorsicht, Es gibt gleichschenklige Trapeze, deren Diagonalen Symmetrieachsen sind.
Yellow
1. Ein Viereck ist ein gleichschenkliges Trapez wenn sich die Mittelsenkrechten in einem Punkt schneiden.
2. Ein Viereck ist ein gleichschenkliges Trapez, wenn die Mittelsenkrechten der parallelen Seiten identisch sind.
--Yellow 22:34, 27. Jan. 2013 (CET)
--*m.g.* 19:05, 3. Feb. 2013 (CET)
zu 1.
Was ist damit? Mittelsenkrechten schneiden sich in genau einem Punkt!
zu 2.
Oberbegriff Viereck oder doch besser Trapez?
Sallyfield
Ein gleichschenkliges Trapez ist ein Viereck mit zwei zueinander parallelen Seiten, wobei diese eine gemeinsame Mittelsenkrechte haben
(Sallyfield)
Sweetnightmare5
Anm: Wenn zwei Strecken oder wie in unserem Falle Seiten eine gemeinsame Mittelsenkrechte haben, sind die Seiten automatisch Parallel, es sei denn sie sind identisch, was aber in einem Viereck nicht vorkommen kann.--Sweetnightmare5 15:12, 29. Jan. 2013 (CET)
Sweetnightmare5
Ein Trapez ist dann gleichschenklig, wenn zwei Mittelsenkrechten der Seiten des Trapezes identisch sind. --[[Benutzer:|Sweetnightmare5]] 13:53, 28. Jan. 2013 (CET)
--*m.g.* 19:14, 3. Feb. 2013 (CET)=
perfekt, funktioniert sogar, wenn als Oberbegriff Viereck und nicht Trapez gemommen wird, s. Bemerkungen zu Sallyfield unten
LilPonsho
Ein Trapez, welches einen Umkreis besitzt, heißt gl. Trapez.--LilPonsho 20:40, 28. Jan. 2013 (CET)
Ein Trapez, bei dem sich die gegenüberliegenden Winkel zu 180 ergänzen, heißt gl. Trapez. --LilPonsho 20:40, 28. Jan. 2013 (CET)
--*m.g.* 19:23, 3. Feb. 2013 (CET)
beides korrekt
Sweetnightmare5
Gleich dazu:
Ein Sehnenviereck mit einem Paar paralleler Seiten ist ein gleichschenkliges Trapez --Sweetnightmare5 15:22, 29. Jan. 2013 (CET)
--*m.g.* 19:23, 3. Feb. 2013 (CET)
korrekt
Sallyfield
Hier müssten wir die Definition folgendermaßen ändern: Ein symmetrisches Trapez ist ein Viereck mit zwei zueinander parallelen Seiten, wobei diese eine identische Mittelsenkrechte haben(Sallyfield)
--*m.g.* 19:20, 3. Feb. 2013 (CET)
Versuchen Sie einmal ein Viereck zu konstruieren, in dem zwei Seiten eine identische Mittelsenkrechte haben, und das kein Trapez ist.
Sei  die Mittelsenrechte von
die Mittelsenrechte von  und von
und von  . Da wir es mit einem Viereck zu tun haben, sind die beiden Seiten nicht identisch. Weil
. Da wir es mit einem Viereck zu tun haben, sind die beiden Seiten nicht identisch. Weil  senkrecht auf
senkrecht auf  und auf
und auf  steht, müssen
steht, müssen  und
und  nach der Umkehrung des Stufenwinkelsatzes ...
nach der Umkehrung des Stufenwinkelsatzes ...
siehe auch Bemerkung von Sweetnightmare5 oben
müsst das b nicht c heißen?
--Yellow 23:44, 3. Feb. 2013 (CET)