Der Inkreis und die Winkelhalbierenden eines Dreiecks (SoSe 11)

Winkelhalbierenden eines Dreiecks

Definition XV.1 : (Winkelhalbierenden eines Dreiecks)

Unter den Winkelhalbierenden eines Dreiecks versteht man die Winkelhalbierenden der Innenwinkel des Dreiecks.

Satz XV.1a : (Abstand eines Punktes einer Winkelhalbierenden zu den Schenkeln des Winkels)

Jeder Punkt der Winkelhalbierenden eines Winkels hat zu den Schenkeln des Winkels jeweils ein und denselben Abstand.

Satz XV.1b : (Umkehrung von Satz XV.1a)

(das können Sie selbst:)

Jeder Punkt im Inneren eines Winkels, der zu den Schenkeln jeweils denselben Abstand hat, ist die Winkelhalbierende des Winkels. --Teufelchen 15:53, 12. Jul. 2011 (CEST)

schreiben Sie besser: ...gehört zur Winkelhalbierenden des
 Winkels. Nach Ihrer Formulierung könnte sonst eine Winkelhalbierende aus einem einzigen Punkt
 bestehen.--Schnirch 14:27, 17. Jul. 2011 (CEST)

Winkelhalbierendenkriterium

(auch das sollten Sie jetzt selbst hinbekommen:)

Der Strahl 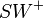$\ SW^{+}$ ist genau dann Winkelhalbierende des Winkels $\angle ASB$ , wenn jeder Punkt der Winkelhalbierenden zu den Schenkeln ein und denselben Abstand hat. --Teufelchen 23:24, 11. Jul. 2011 (CEST)

schreiben Sie besser: ...wenn jeder Punkt des Strahls zu den
 Schenkeln..., denn Sie wollen ja die Bedingung beschreiben, die für den Strahl gelten muss, damit er
 Winkelhalbierende ist--Schnirch 14:36, 17. Jul. 2011 (CEST)

oder
Genau dann, wenn jeder Punkt der zu den Schenkeln eines Winkels ein und denselben Abstand hat, dann liebt die Winkelhalbierenden im Inneren des Winkels. --Teufelchen 16:02, 12. Jul. 2011 (CEST)

Versuchen Sie doch mal die folgende Formulierung zu vervollständigen:--Schnirch 14:41, 17. Jul. 2011 (CEST)
Es sei P ein Punkt aus dem Inneren des Winkels $\alpha$. P ist genau dann ein Punkt der...

Es sei P ein Punkt aus dem Inneren des Winkels $\alpha$. P ist genau dann ein Punkt der Winkelhalbierenden, wenn er zu den beiden Schenkeln des Winkels $\alpha$ ein und denselben Abstand hat.--Bushido

Satz XV.2 : (Schnittpunkt der Winkelhalbierenden eines Dreiecks)

Die Winkelhalbierenden eines Dreiecks schneiden sich in genau einem Punkt.

Beweis von Satz XV.2 mit Hilfe des Winkelhalbierendenkriteriums: Versuchen Sie es selbst:

Inkreis eines Dreiecks

Definition XV.2 : (Tangente an einen Kreis)

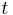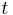Eine Gerade $\ t$ berührt einen Kreis $\ k$, wenn sie mit dem Kreis $\ k$ genau einen Punkt $\ P$ gemeinsam hat. Die Gerade $\ t$ heißt Tangente im Punkt $\ P$.
es musst noch ergänzt werden, dass der Punkt P Berührpunkt heißt. Mathegott 16:53, 19. Jul. 2011 (CEST)

Definition XV.3 : (Strecke berührt Kreis)

Eine Strecke $\overline{AB}$ berührt einen Kreis $\ k$, wenn sie... (ergänzen Sie!)

Teilmenge der Tangente AB des Kreises ist. --Teufelchen 16:22, 13. Jul. 2011 (CEST)

Das kann stimmen, gilt aber nicht allgemein.--Tutorin Anne 19:46, 18. Jul. 2011 (CEST)

Eine Strecke AB berührt einen Kreis k, wenn sie Teilmenge der Tangente AB des Kreises k ist und der Berührpunkt zu der Strecke AB gehört.Mathegott 16:53, 19. Jul. 2011 (CEST)
So könnte man dies definieren.
Aber zunächst muss man sich fragen, welche der Strecken sollen zur Definition gehören, welche möchte man ausschließen?

Welches ist eine Strecke, die den Kreis berührt?
$\overline{AB}$?
$\overline{ED}$?
$\overline{FG}$?
$\overline{BC}$?
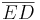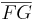--Tutorin Anne 17:34, 19. Jul. 2011 (CEST)

Definition XV.4 : (Inkreis eines Dreiecks)

Ein Kreis, der alle drei Seiten eines Dreiecks in jeweils genau einem Punkt berührt, heißt Inkreis des Dreiecks.

Satz XV.3 : (Existenz und Eindeutigkeit des Inkreises)

...ergänzen Sie!

Jedes Dreieck hat genau einen Inkreis.--Teufelchen 23:26, 11. Jul. 2011 (CEST)