Diskussion:Lösung von Aufgabe 10.2: Unterschied zwischen den Versionen
| Zeile 12: | Zeile 12: | ||
Indirekt müsste man Annehmen, dass es noch eine weitere Senkrechte l gibt, die durch den Punkt P geht und senkrecht auf g steht. Was aber gleich ein Widerspruch zum Winkelkonstruktionsaxiom wäre. Oder ein Widerspruch zu Axiom I.2, dass durch zwei Punkte genau eine Gerade geht.<br /> | Indirekt müsste man Annehmen, dass es noch eine weitere Senkrechte l gibt, die durch den Punkt P geht und senkrecht auf g steht. Was aber gleich ein Widerspruch zum Winkelkonstruktionsaxiom wäre. Oder ein Widerspruch zu Axiom I.2, dass durch zwei Punkte genau eine Gerade geht.<br /> | ||
--[[Benutzer:Löwenzahn|Löwenzahn]] 09:23, 3. Jul. 2010 (UTC) | --[[Benutzer:Löwenzahn|Löwenzahn]] 09:23, 3. Jul. 2010 (UTC) | ||
| + | |||
| + | |||
| + | Ich hab lang nichts geschrieben, aber ich merke, dass ich immer noch nicht zufrieden bin. Im ersten Absatz steht | ||
| + | :"Die Winkel die daraus entstehen sind <math>| \angle CPB^{-}| und \angle CPB^{+}| </math>. Die beiden Winkel haben somit einen Strahl <math>{PC^{+}} </math> und eine Gerade PB gemeinsam, die aus den Schenkeln gebildet wird." | ||
| + | Genau da liegt meines Erachtens die falsche Begründung. Nur weil die Winkel einen Schenkel gemeinsam haben, müssen die beiden anderen Schenkel noch nicht eine Gerade bilden. Das pa | ||
Version vom 8. Juli 2010, 22:34 Uhr
Ich habe noch ein Problem mit der Eindeutigkeit. Löwenzahn, du hast ja geschrieben "Da es nach dem Winkelkonstruktionsaxiom genau eine Gerade gibt, ist die Eindeutigkeit bereits gezeigt." Das ist mir noch nachgegangen. Es gibt nach dem Winkelkonstruktionsaxiom genau ein Strahl pro Halbebene. Zu jedem Strahl gehört eine Gerade, demnach gäbe es zwei Geraden. Jetzt versteht mich nicht falsch, es ist mir schon klar, dass es nur eine gibt, aber die Begründung muss m.E. über das Winkelkonstruktionsaxiom hinausgehen. *m.g.* hat ja gesagt man kann da noch einen indirekten Beweis führen, wenn es einem nicht ganz wohl damit ist. Und mir ist tatsächlich nicht ganz wohl damit. Aber ich denke, indirekt oder nicht, es muss über die Definiton von rechten Winkeln gehen, dass sie nämlich kongruent zu ihren Nebenwinkeln sind. Und Nebenwinkel sind's nur dann, wenn die beiden Strahlen eben zu genau einer Gerade gehören.
--Sternchen 22:59, 2. Jul. 2010 (UTC)
Wir haben ja die Strahlen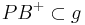 
und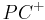 
nach dem Winkelkonstruktionsaxiom. Die Winkel die daraus entstehen sind 
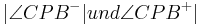. Die beiden Winkel haben somit einen Strahl
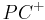und eine Gerade PB gemeinsam, die aus den Schenkeln gebildet wird. Somit ist die Definition Nebenwinkel erfüllt.
Und durch die Äquivalenz "Ein Winkel ist genau dann ein rechter Winkel, wenn er die Größe 90 hat", die sich aus Satz V.3 und V.4 (Skript Winkelmessung) ergibt und wir ja durch die Winkelkonstruktion festgelegt haben, dass der Winkel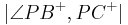 
das Maß 90 hat, ergibt sich, dass auch sein Nebenwinkel 
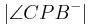das Maß 90 hat. Somit ist auch die Defintion rechter Winkel erfüllt.
Aber dann hat man doch immernoch nicht gezeigt, dass die Senkrechte eindeutig ist, sondern nur, dass sie im rechten Winkel auf g steht.
Indirekt müsste man Annehmen, dass es noch eine weitere Senkrechte l gibt, die durch den Punkt P geht und senkrecht auf g steht. Was aber gleich ein Widerspruch zum Winkelkonstruktionsaxiom wäre. Oder ein Widerspruch zu Axiom I.2, dass durch zwei Punkte genau eine Gerade geht.
--Löwenzahn 09:23, 3. Jul. 2010 (UTC)
Ich hab lang nichts geschrieben, aber ich merke, dass ich immer noch nicht zufrieden bin. Im ersten Absatz steht
- "Die Winkel die daraus entstehen sind 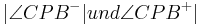. Die beiden Winkel haben somit einen Strahl 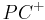und eine Gerade PB gemeinsam, die aus den Schenkeln gebildet wird."
Genau da liegt meines Erachtens die falsche Begründung. Nur weil die Winkel einen Schenkel gemeinsam haben, müssen die beiden anderen Schenkel noch nicht eine Gerade bilden. Das pa
