Diskussion:Quiz der Woche 8 (SoSe 11)

Worin besteht das Problem der 15. Frage?

&Frage15=Sei R eine Relation auf Z, für die gilt: a~b ⇔ a mod 3 = b mod 3. Was stimmt dann nicht? &A15=(6,9) und (1,4) sind in R enthalten. &B15=Jedes Element in R kann Repräsentant einer Äquivalenzklasse sein. &C15=Es gibt genau 3 Äquivalenzklassen. &D15=R ist reflexiv und symmetrisch aber nicht transitiv. &AW15=D

Der obige Text steht hinter der 15. Frage.

Die Relation: Die ganze Zahl a steht mit der ganzen Zahl b in Relation :gdw. a lässt bei Division durch 3 denselben Rest wie b bei Division durch 3.

Antwort A:

Sowohl 6 als auch 9 sind durch 3 teilbar: Rest 0. Das Paar (6,9) gehört zur Relation.

1 und 4 lassen bei Division durch 3 den Rest 1: (1,4) gehört zur Relation.

Antwort B:

Alles klar, ich hab's kapiert. Die Antwort soll wohl "Jedes Element aus 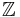$\mathbb{Z}$ ..." heißen. Also lesen Sie R als Z. Jede ganze Zahl ist Repräsentant einer Äquivalenzklasse nach unserer Relation a lässt bei Division durch 3 denselben Rest wie b bei Division durch 3.

Antwort C:

Sei 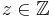$z \in \mathbb{Z}$ Dann lässt 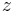$\ z$ bei Division durch 3 entweder keinen Rest, den Rest 1 oder den Rest 2. Damit gibt es genau drei Restklassen.

Antwort D:

natürlich handelt es sich bei unserer Relation um eine ÄR. Wenn a bei Division durch 3 densleben Rest lässt wie b bei Division durch 3 und b bei Division durch 3 denselben Rest lässt wie c bei Division durch 3, dann lässt selbstverständlich a bei Division durch 3 denselben Rest wie c bei Division durch 3.

Im Rahmen des Quiz wäre D bezüglich der 15. Frage die korrekte Antwort unter der Bedingung, dass Antwort B berichtigt wird.

--*m.g.* 18:16, 9. Jul. 2011 (CEST)