Eigentlich ganz einfach und doch so kompliziert: Punkte, Geraden, Ebenen
Inhaltsverzeichnis |
Was ist ein Punkt?
| „Man muss jederzeit an Stelle von ‚Punkten‘, ‚Geraden‘, ‚Ebenen‘, ‚Tische‘, ‚Stühle‘, ‚Bierseidel‘ sagen können.“
David Hilbert (1862-1943) |
Auf die Frage, was denn eine Strecke sei, erhält man oft zur Antwort, es handle sich dabei um die kürzeste Verbindung zwischen zwei Punkten. Strecken sind offenbar durch Punkte bestimmt. Was aber ist ein Punkt? Diese Frage bewegte bereits im Altertum die Mathematiker, die damals zumeist auch Philosophen waren:
| Plato:
427 – 347 v.Chr. „Ein Punkt ist der Anfang einer Linie.“ | |
| Aristoteles:
384 – 322 v.Chr. „Ein Punkt ist eine unteilbare Einheit, die eine Position besitzt.“ | |
| Euklid:
um 365 bis ca. 300 v. Chr. „Was keine Teile hat ist ein Punkt.“ |
Bei allem Respekt vor den Leistungen dieser Herren, ihre „Definitionen“ des Begriffes Punkt schaffen dem Erkenntnissuchenden nur für einen kurzen Moment Erleichterung. Danach quält ihn erneut die Gewissheit, eigentlich nichts zu wissen.
- Was ist eine Linie?
- Was ist der Anfang von etwas von dem ich nicht weiß, was es ist?
- Was meint Aristoteles mit seiner Einheit?
- Wenn ich schon nicht weiß, was mit Einheit gemeint ist, wie soll ich dann begreifen, was eine unteilbare Einheit ist?
- Wer oder was zum Teufel hat keine Teile?
Betrachten wir doch einfach solche Objekte, mit deren Definition wir „weniger“ Schwierigkeiten haben.
- Ein Quadrat ist ein Rechteck mit 4 gleichlangen Seiten.
- Ein Rechteck ist ein Parallelogramm mit einem rechten Innenwinkel.
- Ein Parallelogramm ist ein Trapez mit zwei Paaren paralleler Seiten.
- Ein Trapez ist ein Viereck mit einem Paar paralleler Seiten.
- Ein Viereck ist die Vereinigungsmenge von vier Strecken, wobei je drei der Endpunkte dieser Strecken nicht auf ein und derselben Geraden liegen.
Aus Gründen der Vollständigkeit wäre jetzt zu klären, was eine Strecke ist. Damit sind wir auf demselben Stand, wie zu Anfang dieser Ausführungen. Für den Begriff der Strecke brauchen wir wieder den Begriff des Punktes. Die Herren Plato, Aristoteles und Euklid waren diesbezüglich sehr bemüht aber letztlich nicht wirklich hilfreich. Irgendwann muss die Sache einmal „auf den Punkt gebracht“ werden:
Punkte, Geraden und Ebenen lassen sich nicht wie Quadrate und Kreise definieren. Trotzdem haben wir gewisse Vorstellungen von ihren Eigenschaften: Durch zwei verschiedene Punkte geht genau eine Gerade. In diesem Sinne erfahren die abstrakten Grundbegriffe eine Präzisierung. Beweisen kann man die Eigenschaften der Grundobjekte freilich nicht. Es sind unbeweisbare Grundtatsachen bzw. Grundannahmen. Der Mathematiker formuliert sie als Forderungen und nennt diese dann Axiome.
Axiome und undefinierte Grundbegriffe
Die Bezeichnung Geometrie kommt aus dem Griechischen und bedeutet soviel wie Erdvermessung. Geometrie kann damit zunächst als die Lehre vom uns umgebenden Anschauungsraum verstanden werden.
Schon wieder so ein verwaschener Begriff: Anschauung. Da legen wir doch gleich noch eins nach: gesunder Menschenverstand. Dann war noch vom Raum die Rede und schon ergibt sich eine Assoziationskette: Johannes Kepler, Galileo Galilei, „Und sie bewegt sich doch!“, Inquisition, Rehabilitation 1992.
Eine gewisse Skepsis erscheint im Zusammenhang mit Anschauung angebracht. Damit sind wir in der Zwickmühle. Zum einen müssen wir unsere Grundannahmen der Anschauung entnehmen. Zum anderen wissen wir um damit verbundene eventuelle Unzulänglichkeiten. Die Geometer versuchen die Unabwägbarkeiten zu minimieren:
- Als Axiome werden nur sehr einfache, plausible Aussagen zugelassen, von deren Richtigkeit man mal wohl „hundertprozentig“ überzeugt sein kann.
- Die Anzahl der unbewiesenen Grundannahmen wird so gering wie möglich gewählt. Gleiches gilt für die undefinierten Grundbegriffe.
- Alle weiteren Elemente der Geometrie werden rein deduktiv aus den Axiomen und Grundbegriffen abgeleitet.
Ein Schema soll diesen Ansatz demonstrieren:
Euklid kommt die Ehre zu, als erster auf diese Weise die Geometrie des Anschauungsraumes begründet zu haben. Sich vor den Leistungen Euklids verneigend spricht man von Euklidische Geometrie.
Bis zu einer im modernen Sinne durchgängig korrekten axiomatischen Begründung der Euklidischen Geometrie sollten seit Euklid jedoch noch 2300 Jahre vergehen. 1899 stellte David Hilbert in seiner Arbeit „Grundlagen der Geometrie“ das erste logisch völlig exakte Axiomensystem der Euklidischen Geometrie auf. Die „Grundlagen der Geometrie“ waren im übrigen eine Festschrift aus Anlass der Enthüllung des Gauß‑Weber-Denkmals in Göttingen.
Besser als der Meister kann man die Dinge wohl nicht erläutern:
„Erklärung:Wir denken drei verschiedene Systeme von Dingen. Die Dinge des ersten Systems nennen wir Punkte und bezeichnen sie mit A, B, C…;die Dinge des zweiten Systems nennen wir Geraden und bezeichnen sie mit a, b, c…;die Dinge des dritten Systems nennen wir Ebenen und bezeichnen sie mit 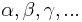 ; …Wir denken die Punkte Geraden und Ebenen in gewissen gegenseitigen Beziehungen und bezeichnen diese Beziehungen durch Worte wie ‚liegen‘, ‚zwischen‘, ‚parallel‘, ‚kongruent‘, ‚stetig‘; die genaue und vollständige Beschreibung erfolgt durch die Axiome der Geometrie.“
; …Wir denken die Punkte Geraden und Ebenen in gewissen gegenseitigen Beziehungen und bezeichnen diese Beziehungen durch Worte wie ‚liegen‘, ‚zwischen‘, ‚parallel‘, ‚kongruent‘, ‚stetig‘; die genaue und vollständige Beschreibung erfolgt durch die Axiome der Geometrie.“
(Hilbert, S. 2)
Auch wenn der Anschauungsraum bei der Formulierung der Axiome und der Festlegung der undefinierten Grundbegriffe Pate stand, löst sich die Theorie dann von der Anschauung. Geometrie wird zu einem eigenständigen komplexen System. In gewisser Weise haben die Mathematiker „Gott gespielt“ und eine eigene Welt erschaffen. Diese Welt ist relativ überschaubar. Sie beruht auf 5 Axiomengruppen und beinhaltet alles, was man rein deduktiv aus diesen mit den Mitteln der mathematischen Logik ableiten kann.
Geometrie in der Ebene
Punkte und Geraden
Wir gehen von einer nichtleeren Menge 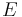 aus, die Ebene genannt wird. Die Elemente von
aus, die Ebene genannt wird. Die Elemente von 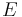 heißen Punkte und werden mit
heißen Punkte und werden mit 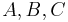 … bezeichnet. Ferner möge eine weitere nichtleere Menge
… bezeichnet. Ferner möge eine weitere nichtleere Menge 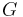 existieren, deren Elemente wir Geraden nennen und mit
existieren, deren Elemente wir Geraden nennen und mit 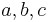 … bezeichnen wollen.
Unsere erste Vorstellung von Geraden ist, dass diese aus Punkten bestehen:
… bezeichnen wollen.
Unsere erste Vorstellung von Geraden ist, dass diese aus Punkten bestehen:
AXIOM I/0
- Geraden sind Punktmengen.
Die weiteren Eigenschaften von Punkten und Geraden werden durch die folgenden (Inzidenz)Axiome festgelegt.
AXIOM I/1(Axiom von der Geraden)
- Zu zwei beliebigen verschiedenen Punkten gibt es genau eine Gerade, die die beiden Punkte enthält.
Axiom I/1 liefert eine weitere Bezeichnungsmöglichkeit von Geraden. Eine Gerade g, die durch zwei verschiedene Punkte A und B eindeutig bestimmt ist wird auch mit AB bezeichnet.
AXIOM I/2
- Zu jeder Geraden gibt es wenigstens zwei Punkte, die dieser Geraden angehören.
Für die weitere Formulierung von Axiomen ist es sinnvoll, den Begriff kollinear zu definieren.
Definition I/2: (kollinear)
- Eine Menge von Punkten heißt kollinear, wenn es eine Gerade gibt, die alle Punkte der Menge enthält.
- Schreibweise: koll(A, B, C, ...) Sollten die Punkte A, B, C einer Menge nicht kollinear sein, so schreibt man:nkoll(A, B, C)
AXIOM I/3
- Es gibt wenigstens 3 Punkte, die nicht kollinear sind.
Folgerungen aus den Axiomen der ebenen Inzidenzgeometrie
Viel wurde noch nicht axiomatisch gefordert. Dementsprechend werden wir auch noch nicht viele interessante Aussagen aus den Axiomen ableiten können. Wegen der geringen Anzahl von Axiomen ist es jedoch recht einfach, die Idee des axiomatischen Arbeitens zu verdeutlichen.
Folgende Sätze lassen sich aus den Axiomen I/0 bis I/3 ableiten.
Satz I.1
- Es seien g und h zwei Geraden. Wenn g und h nicht identisch sind, haben sie höchstens einen Punkt gemeinsam.
Beweis von Satz I.1
- Voraussetzung: Es seien g und h zwei Geraden, die nicht identisch sind.
- Fall 1:
- Die Geraden g und h haben keinen Punkt gemeinsam. In diesem Fall ist nichts weiter zu zeigen, denn sie haben damit nicht mehr als einen Punkt gemeinsam.
- Fall 2:
- Die Geraden g und h schneiden sich in einem Punkt P.
- Wir haben zu zeigen, dass sie keinen weiteren Punkt gemeinsam haben.
- Wir führen den Beweis indirekt und nehmen an, dass die Geraden g und h einen weiteren von P verschiedenen Punkt Q gemeinsam haben.
- Das Axiom I/1 sagt aus, dass durch zwei verschiedene Punkte genau eine Gerade geht. Da die beiden Punkte P und Q verschieden sind, kann auf sie dieses Axiom angewandt werden.
- Die Gerade g geht durch P und Q und die Gerade h geht durch P und Q. Da es nun eine und nur eine Gerade gibt, die durch P und Q geht, müssen die beiden Geraden g und h identisch sein. Das ist allerdings ein Widerspruch zur Voraussetzung, dass g und h nicht identisch sind.
- Die Annahme, dass ein weiterer gemeinsamer Punkt Q der beiden Geraden g und h existiert, ist damit zu verwerfen.
Die Aussage des Satzes I.1 ist eine Implikation, d.h. sie hat die folgende Form:Wenn Aussage A so Aussage B.
Denselben Wahrheitswert wie eine Implikation hat die sogenannte Kontraposition der Implikation:
Wenn nicht Aussage B so nicht Aussage A.
Satz I.2: (Kontraposition von Satz I.1)
- Es seien g und h zwei Geraden.
Wenn g und h mehr als einen Punkt gemeinsam haben, so sind g und h identisch.
Da eine Implikation und ihre Kontraposition im Wahrheitsgehalt übereinstimmen und Satz I.2 die Kontraposition von Satz I.1 ist, bräuchten wir nach dem Beweis von Satz I.1 den Satz I.2 nicht mehr zu beweisen.
Zur Übung und auch aus dem Grund, dass man Satz I.2 direkt beweisen kann, soll Satz I.2 noch einmal bewiesen werden.
Beweis von Satz I.2
- Es seien
 und
und 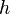 zwei Geraden.
zwei Geraden.
- Voraussetzung: g und h haben mehr als einen Punkt gemeinsam.
- Es seien dieses die Punkte P und Q.
- Wir haben zu zeigen, dass die beiden Geraden g und h identisch sind.
- Dieses folgt unmittelbar aus Axiom I/1.
Satz I.3: (Existenz von drei Geraden)
- Es existieren mindestens drei paarweise verschiedene Geraden.
Beweis von Satz I.3
- Nach Axiom I/3 existieren drei Punkte A, B und C mit nkoll(A, B, C).
- Die drei Punkte A, B und C sind paarweise verschieden. Wären nämlich zwei der Punkte identisch, so würde nach Axiom I/1 sofort koll(A, B, C) folgen.
- Nach Axiom I/1 existieren die Geraden AB, BC und AC.
- Wenn wir zeigen können, dass keine zwei dieser Geraden nicht identisch sind, ist die Behauptung bewiesen.(WÄRE ES NICHT EIGENTLICH:...dass keine zwei dieser Geraden identisch sind...ALSO OHNE DAS NICHT???)
- Wir nehmen an, dass etwa AB und BC identisch sind. In diesem Fall wären die Punkte A, B und C Punkte ein und derselben Geraden. Dieses wäre jedoch ein Widerspruch zur Aussage von Beweisschritt (1).
- Dementsprechend ist es nicht möglich, dass je zwei der drei Geraden AB, BC und AC identisch sein.
Viel mehr an einigermaßen interessanten Sätzen ist aus den ebenen Inzidenzaxiomen nicht herauszuholen. Wenn dem Thema Inzidenz trotzdem eine ganze Vorlesung in unseren Untersuchungen eingeräumt wird, so liegt das mehr daran, dass sich anhand dieser wenigen einfachen Aussagen recht gut die Prinzipien axiomatischen Arbeitens in der Geometrie erläutern lassen.


