GeometrieUndUnterrichtSS2019 03: Unterschied zwischen den Versionen
(→Literaturhinweise) |
(→Ergebnisse der Nachbereitung) |
||
| Zeile 71: | Zeile 71: | ||
|- | |- | ||
| | | | ||
| − | Beispiel | + | Betrachten Sie die folgende Situation: |
| + | |||
| + | Für seine Mathematikhausaufgaben dividiert Lukas die Zahl 3 durch 1/3. Er wendet die Rechenregeln zur Bruch-Division richtig an und erhält das Ergebnis 9. Lukas fragt sich: „Warum kann das Ergebnis der Division größer sein als der Dividend?“ | ||
| + | |||
| + | 1. Wie erklären Sie sich Lukas‘ Denkfehler? Beziehen Sie das Konzept der Grundvorstellungen in die Beantwortung ein. | ||
| + | |||
| + | 2. Mit welchem veranschaulichenden Beispiel könnte diesem Denkfehler entgegen gewirkt werden? | ||
| + | |||
| + | 3. Könnte man Lukas den Sachverhalt auch anhand von geometrischen Figuren erklären? | ||
|| | || | ||
| − | + | 1. Das Problem zeigt, wie wichtig neben den Rechenverfahren auch inhaltliche Vorstellungen mathematischer Inhalte, wie z.B. der Division, sind. Diese inhaltlichen Vorstellungen werden in der Mathematikdidaktik als Grundvorstellungen bezeichnet. Sie beschreiben die möglichst konkrete, inhaltliche ‚Interpretation‘ von mathematischen Objekten und Sachverhalten und sollen dabei helfen, ein tieferes Verständnis der mathematischen Verfahrensweisen zu erhalten. | |
| + | |||
| + | Lukas verfügt nicht über ausreichende Grundvorstellungen der Division durch Brüche, weil er auf die Vorstellung der Division als ‚Verteilen‘ fixiert ist. Würde er sich stattdessen die Frage stellen, wie oft 1/3 in 3 ‚passt‘, und die Division damit als Frage des richtigen Aufteilens interpretieren, wäre sein Vorstellungsproblem gelöst. | ||
| + | |||
| + | 2. Um Lukas‘ Denkfehler vorzubeugen, müsste bei den SuS die Grundvorstellung der Division als ‚Aufteilen‘-Operation geweckt werden. Zur Veranschaulichung des Sachverhaltes eignet sich beispielsweise die folgende Problemstellung: „3 Liter Apfelsaft sind in 1/3-l-Flaschen umzufüllen. Wie viele Flaschen werden hierfür benötigt?“ | ||
| + | |||
| + | 3. Die folgende Möglichkeit bietet sich dazu an, Lukas den Sachverhalt bzw. die Grundvorstellung der Division als ‚Aufteilen‘-Operation anhand von geometrischen Figuren zu vermitteln: Gegeben seien 3 identische, geometrische Figuren (z.B. Kreise, Rechtecke, Quadrate), die von den SuS in jeweils 3 gleich große Teile zerlegt werden sollen. Anschließend kann gezählt werden, wie viele ‚Drittel‘ in die 3 Figuren 'passen'. | ||
| + | |||
|| | || | ||
| − | + | Die Aufgabe eignet sich dazu, das didaktische Konzept der 'Grundvorstellungen' anwendungsorientiert abzufragen. | |
<!-- === Abgabe MAX MUSTER Ende ============================================================================================================= --> | <!-- === Abgabe MAX MUSTER Ende ============================================================================================================= --> | ||
<!-- === Abgabe MARA MUSTER Anfang ========================================================================================================== --> | <!-- === Abgabe MARA MUSTER Anfang ========================================================================================================== --> | ||
Version vom 14. Mai 2019, 21:22 Uhr
Inhaltsverzeichnis |
Vorbereitungsauftrag
Entwerfen Sie eine Unterrichtsaktivität für die Einführung bzw. einführenden Erarbeitung des Begriffs Parallelogramm. Ziel der Unterrichtsaktivität ist die Kenntnis der Begriffsdefinition. Gehen Sie von einer generischen (Real-)Schulklasse der sechsten Jahrgangsstufe aus. Gehen Sie davon aus, dass die Schüler*innen aus der fünften Jahrgangsstufe bereits in der Lage sind, 'Parallelität' im Kontext paralleler Geraden und Vierecke, Quadrate und Rechtecke identifizieren können. Beachten Sie auch den gemeinsamer Bildungsplan für die Sekundarstufe I des Landes Baden-Württemberg.
In der Didaktischen Werkstatt Mathematik und Informatik der PH Heidelberg finden Sie u.a. eine Sammlung von verschiedenen Schulbüchern, die Sie gerne zur Inspiration nutzen können.
Sitzungsmaterialien
- Begleitfolien der Seminarsitzung vom 10.05.2019
- Screenshot „Das Problem der Apfelbauern“ (Mittelsenkrechte als Äquidistanzkurve)
Dokumentation der Sitzung
Zusammenfassung und Bezug zu den Bildungsstandards
Inhaltlicher Input
Arbeitsphase
Zusatzmaterial
Als zusätzliche Übungsgelegenheit für die Unterstützung der Begriffslernens mit Blick auf das Operative Prinzip finden Sie die Aktivität „Schwarze Kisten am Dreieck“ in der GeoGebra.org-Gruppe des Seminars. Entwerfen Sie hierzu ein Arbeitsblatt zur angeleiteten Exploration des Applets. Versuchen Sie dabei explizite Handlungs-, Beobachtungs- und hypothesengenerierende Anweisungen zu geben.
Nachbereitungsauftrag
Entwerfen Sie eine Prüfungsfrage bzw. ein kurzes Prüfungsgespräch zu den Sitzungen zum Begriffslernen (I+II). Ihre Frage sollte dabei nicht nur bloße Wissensabfrage sein, sondern auch Anwendungen, Begründungen oder Diskussionen erfordern. (Sollte Ihnen doch nur Aufgaben zur bloßen Wissensabfrage einfallen, entwerfen Sie drei Prüfungsfragen.)
- Formulieren Sie Ihre Prüfungsfrage bzw. den Anlass für das Prüfungsgespräch in der Aufgabenstellung-Spalte.
- Beschreiben Sie ausführlich, wie mögliche (richtige) Antworten auf Ihre Frage aussehen könnten bzw. welche Aspekte in einem Prüfungsgespräch zu dieser Frage angesprochen werden sollten. Tragen Sie dies entsprechend in die Erwartungshorizont-Spalte ein.
- Erläutern Sie kurz, warum Sie diese Aufgabe einen zentralen Aspekt der Sitzung abdeckt und welche Anforderung an Wissen/Kompetenzen die Aufgabe fordert.
Unter den übergreifenden Literaturhinweise sind insbesondere relevant:
- Kapitel 5 „Begriffslernen und Begriffslehren“ in Weigand et. al. (2018). „Didaktik der Geometrie für die Sekundarstufe I“
- Diverse Ausgangspunkte zu Diskussionen über Grundvorstellungen und Darstellungen sind in den ersten Kapiteln von Ludwig et. al. (2015). „Geometrie zwischen Grundbegriffen und Grundvorstellungen“ zu finden.
- Kapitel 4 in Kaenders & Schmitt (2014). „Mit GeoGebra mehr Mathematik verstehen“ bietet Ausgangspunkte zur Diskussion über das Operative Prinzip. Genauso Wittmann (1985): „Objekte-Operationen-Wirkungen: Das operative Prinzip in der Mathematikdidaktik“ In Mathematik lehren.
Mögliche Inspiration können Sie gerne auch weiteren Quellen entnehmen. Zum Beispiel:
- Mason (2009). „The van Hiele levels of geometric understanding.“ In Colección Digital Eudoxus 1.2.
Ergebnisse der Nachbereitung
Tragen Sie die Ergebnisse Ihrer Nachbereitung in die folgende Tabelle ein.
| Aufgabenstellung | Erwartungshorizont | Diskussion |
|---|---|---|
|
Aus algebraischer Sicht ist die folgende Gleichungskette offensichtlich wahr (Assoziativgesetz für Brüche):
|
Die Symbole lassen sich als Formel für die Berechnung des Flächeninhalt eines Dreiecks interpretieren. In ihnen sind sogar verschiedene Beweisideen der Berechnungsformel enthalten, die sich aus der Berechnungsformel des Flächeninhalts des Rechtecks herleiten lassen: Der Flächeninhalt ist das Produkt der Hälfte der Grundseite mit der Höhe bzw. die Hälfte des Produkts aus Grundseite und Höhe bzw. das Produkt der Grundseite mit der Hälfte der Höhe. Anfertigung von Skizzen zu den jeweiligen Interpretationen. Der geometrische Zugang unterstützt das Aufbauen von Grundvorstellungen zur Bruchrechnung (u.a. Multiplikation Zahl-mal-Bruch und Bruch-mal-Zahl) und zum Termbegriff (u.a. Kalkülvorstellung, Gegenstandsvorstellung, Terme als „Bauplan“?). Aufzählung der Aspekte von Grundvorstellungen. Die Diskussion der Gleichungskette aus geometrischer Perspektive verlangt mindestens ein integriertes Begriffsverständnis von Viereck und Dreieck (van-Hiele: 3 Apstraction). Beziehungen zwischen den Figuren Dreieck und Viereck müssen erkannt werden (Begriffsnetz). Schlussfolgerungen finden vermutlich auf informeller Ebene statt (etwa Zerlegungen und Verschiebungen vs. formaler Nachweis der Kongruenz von Teildreiecken und Flächengleichheit kongruenter Dreiecke). Es werden u.a. die folgenden geometrischen Konzepte angesprochen: Strecke, Rechteck, Dreieck, Streckenlänge, Flächeninhalt, Zerlegungsgleichkeit, Translationsinvarianz von Streckenlänge und Flächeninhalt. |
Die Aufgabe bietet Anlass, das Wissen zu folgenden Inhalten abzufragen: Grundvorstellungen, Stufen des Begriffserwerbs (van-Hiele-Modell). Darüber hinaus wird die Anwendung des Stufenmodells gefordert und es ist eine Begründung für die Stufenzuteilung nötig. |
|
Betrachten Sie die folgende Situation: Für seine Mathematikhausaufgaben dividiert Lukas die Zahl 3 durch 1/3. Er wendet die Rechenregeln zur Bruch-Division richtig an und erhält das Ergebnis 9. Lukas fragt sich: „Warum kann das Ergebnis der Division größer sein als der Dividend?“ 1. Wie erklären Sie sich Lukas‘ Denkfehler? Beziehen Sie das Konzept der Grundvorstellungen in die Beantwortung ein. 2. Mit welchem veranschaulichenden Beispiel könnte diesem Denkfehler entgegen gewirkt werden? 3. Könnte man Lukas den Sachverhalt auch anhand von geometrischen Figuren erklären? |
1. Das Problem zeigt, wie wichtig neben den Rechenverfahren auch inhaltliche Vorstellungen mathematischer Inhalte, wie z.B. der Division, sind. Diese inhaltlichen Vorstellungen werden in der Mathematikdidaktik als Grundvorstellungen bezeichnet. Sie beschreiben die möglichst konkrete, inhaltliche ‚Interpretation‘ von mathematischen Objekten und Sachverhalten und sollen dabei helfen, ein tieferes Verständnis der mathematischen Verfahrensweisen zu erhalten. Lukas verfügt nicht über ausreichende Grundvorstellungen der Division durch Brüche, weil er auf die Vorstellung der Division als ‚Verteilen‘ fixiert ist. Würde er sich stattdessen die Frage stellen, wie oft 1/3 in 3 ‚passt‘, und die Division damit als Frage des richtigen Aufteilens interpretieren, wäre sein Vorstellungsproblem gelöst. 2. Um Lukas‘ Denkfehler vorzubeugen, müsste bei den SuS die Grundvorstellung der Division als ‚Aufteilen‘-Operation geweckt werden. Zur Veranschaulichung des Sachverhaltes eignet sich beispielsweise die folgende Problemstellung: „3 Liter Apfelsaft sind in 1/3-l-Flaschen umzufüllen. Wie viele Flaschen werden hierfür benötigt?“ 3. Die folgende Möglichkeit bietet sich dazu an, Lukas den Sachverhalt bzw. die Grundvorstellung der Division als ‚Aufteilen‘-Operation anhand von geometrischen Figuren zu vermitteln: Gegeben seien 3 identische, geometrische Figuren (z.B. Kreise, Rechtecke, Quadrate), die von den SuS in jeweils 3 gleich große Teile zerlegt werden sollen. Anschließend kann gezählt werden, wie viele ‚Drittel‘ in die 3 Figuren 'passen'. |
Die Aufgabe eignet sich dazu, das didaktische Konzept der 'Grundvorstellungen' anwendungsorientiert abzufragen. |
|
Beispiel |
Beispiel |
Beispiel |
Literaturhinweise
- Wittmann (1985): „Objekte-Operationen-Wirkungen: Das operative Prinzip in der Mathematikdidaktik“ In Mathematik lehren.
- Aebli (1985): „Das Operative Prinzip“ In Mathematik lehren. (Zweiter Teil des PDFs)
- Schwank (2003): „Einführung in prädikatives und funktionales Denken“ In ZDM Mathematics Education
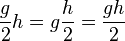 .
.

