GeometrieUndUnterrichtSS2019 04
Inhaltsverzeichnis |
Vorbereitungsauftrag
Vom Volumen zum Flächeninhalt
Denken Sie sich einen mit rechtiger Innenquerschnittsfläche (Würfel, Milchkarton,…). Gesucht ist der Flächeninhalt der Innenquerschnittsfläche (Grundfläche). Zur Verfügung stehen Ihnen Wasser, eine Waage und ein Maßband.
- Wie würden Sie mit Hilfe der gegebenen Hilfsmittel den gesuchten Flächeninhalt bestimmen?
- Übertragen Sie ihr vorgehen auf Körper mit zylinder-förmiger Innenquerschnittsfläche (Tasse, Regentonne, Mülleimer,…) und auf allgemeine Zylinder.
- In dieser Aufgabe wurde das Problem der Flächenmessung auf das Problem der Volumenmessung zurückgeführt. Aus sicht der gewöhnlichen Sequenzierung der mathematischen Inhalte in der Sekundarstufe erscheint dieses Vorgehen zunächst fragwürdig. Erläutern Sie, warum das Problem der Volumenmessung im Alltag tatsächlich das einfacherere Problem ist.
Vom Flächeninhalt zum Volumen
Lesen Sie den Abschnitt „Prinzip von Cavalieri, Satz von Dehn und Pyramidenvolumen“ aus dem Skript zur „Didaktik der Mathematik in der Sek. I“, Kapitel „Didaktik der Geometrie“, von Prof. Dr. Jürgen Roth (Universität Koblenz Landau).
- Vollziehen Sie die Argumente und Beweise der Argumentationslinie Nachweis der Gültigkeit der Volumenformel mit dem Satz von Cavalieri nach.
- Vollziehen Sie die Argumente und Beweise der Argumentationslinie Nachweis der Gültigkeit der Volumenformel mit Stufenkörpern nach.
- Für welchen Unterrichtsgang würden Sie sich in Ihrem Unterricht entscheiden? Warum?
Vorbereitungsauftrag (Zusatz)
Der Satz von Fubini ist ein Satz über die Möglichkeit der Berechnung von Doppelintegralen durch iterative Integration:
Bearbeiten Sie die folgenden Aufträge.
- Wiederholen Sie den Satz von Fubini aus Ihrer entsprechenden Mathematik-Vorlesung (vermutlich Analysis, Maßtheorie, Wahrscheinlichkeitstheorie, Funkionalanalysis o.Ä.).
- Formulieren Sie den Satz von Fubini für folgenden Spezialfall: Es sei
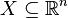 ein abgeschlossener Quader, und
ein abgeschlossener Quader, und 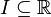 ein abgeschlossenes Intervall. Ferner sei
ein abgeschlossenes Intervall. Ferner sei 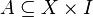 messbar. Wir betrachten für
messbar. Wir betrachten für 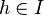 die Mengen
die Mengen 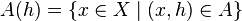 . Wie können Sie
. Wie können Sie 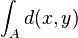 berechnen?
berechnen?
- Für das Prinzip von Cavalieri findet man in Schulbüchern die unten stehende Formulierung. Verwenden Sie die hier angesprochene Integrationstheorie, um eine fachmathematisch präzise Formulierung zu erstellen.
- Welche Bestandteile der Schulbuch-üblichen Formulierung entsprechen welchen Bestandteilen der fachmathematisch präzisen Formulierung?
Das Prinzip von Cavalieri (für Körper)
Zwei Körper haben das gleiche Volumen, wenn sie gleiche Grundflächeninhalte sowie gleiche Höhen besitzen und sämtliche Schnittflächen im gleichen Abstand parallel zur Grundfläche den gleichen Flächeninhalt haben.
Sitzungsmaterialien
- Begleitfolien der Seminarsitzung vom 17.05.2019
- Vortragsnotizen für die Integration des Paralellograms
- Sie auch Zusatzmaterial Fläche und Volumen auf der Mathematischen Medienplattform des Mathematischen Instituts der Universität Heidelberg.
Dokumentation der Sitzung
Zusammenfassung
Diese Sitzung beschäftigte sich exemplarisch mit der Bestimmung des Flächeninhaltes von Parallelogrammen als Einstieg in den Themenkomplex "Messen". Hiervon ausgehend werden auch komplexere Flächen betrachtet.
Generell wurde angemerkt, dass sich bei diesem Themenkomplex GeoGebra gut zum Veranschaulichen eignen könnte!
Inhaltlicher Input (Einführung)
In den Bildungsstandards von Baden-Württemberg findet sich die Leitidee Messen. In diesem Zusammenhang ist oft auch von den vier Grundprinzipien des Messens die Rede:
- Vergleichsaspekt
- Messe-durch-Auslegen-und-Zählen-Aspekt
- Messgeräte-Aspekt
- Messen-als-Berechnen-Aspekt
[Details, siehe oben verlinkte Sitzungsfolien]
Da die Bestimmung von Flächeninhalt/Volumen als Integration angesehen werden kann [Propädeutik], haben wir uns in der folgenden Arbeitsphase mit der Berechnung des Flächeninhalts von Parallelogrammen [mithilfe der Integrationstheorie] beschäftigt.
Arbeitsphase (Flächeninhalt eines Parallelogramms)
Aufwärmübung - Flächeninhalt eines Rechtecks.
Sei 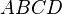 ein Rechteck mit Grundseite
ein Rechteck mit Grundseite  und Höhe
und Höhe  . Dieses Rechteck kann man wie folgt in einem 2D-Koordinatensystem betrachten:
Der Punkt
. Dieses Rechteck kann man wie folgt in einem 2D-Koordinatensystem betrachten:
Der Punkt  ist der Ursprung mit Koordinaten
ist der Ursprung mit Koordinaten 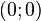 , der Punkt
, der Punkt  entspricht dem Punkt mit Koordinaten
entspricht dem Punkt mit Koordinaten 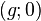 und der Punkt
und der Punkt  entspricht dem Punkt mit Koordinaten
entspricht dem Punkt mit Koordinaten 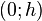 .
Dadurch ist auch bereits
.
Dadurch ist auch bereits  mit
mit 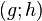 eindeutig festgelegt.
Nun kann die Berechnung des Flächeninhalts als Bestimmung der Fläche Zwischen x-Achse und der Geraden durch
eindeutig festgelegt.
Nun kann die Berechnung des Flächeninhalts als Bestimmung der Fläche Zwischen x-Achse und der Geraden durch  und
und  auf dem Intervall
auf dem Intervall ![[0, g]](/images/math/c/6/1/c61257efbb4f5b53f04b0c810d1b4922.png) betrachte werden. Es handelt sich also um eine simple Integration. Man erhält:
betrachte werden. Es handelt sich also um eine simple Integration. Man erhält:
![F_{ABCD} = \int_0^g h \, dt = [ht]^g_0 = hg](/images/math/0/d/b/0db0d22fade7c39f443679f55ecd0d43.png) .
.
Dieser Ansatz verwendet gerade die Rieman-Integration.
Natürlich wäre aber auch eine Integration über die Höhe  Mittels der Lebesgue-Integration möglich gewesen. Man erhält so:
Mittels der Lebesgue-Integration möglich gewesen. Man erhält so:
![F_{ABCD} = \int_0^h g \, dt = [gt]^h_0 = gh](/images/math/0/8/d/08ddf8e165f47ec21d78b4b75e816538.png) .
.
Flächeninhalt eines Parallelogramms
Im Folgenden werden nun verschiedene Ansätze zur Bestimmung des Flächeninhalts eines Parallelogramms  vorgestellt. Für die exakten Rechnungen sei auf die verlinkten Vortragsnotizen des Dozenten verwiesen.
vorgestellt. Für die exakten Rechnungen sei auf die verlinkten Vortragsnotizen des Dozenten verwiesen.
| Idee | Skizze | Ausführung | Entsprechung |
|---|---|---|---|
| Zerlege das Parallelogramm in drei Teile | Man berechnet 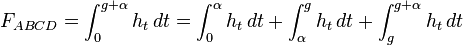 . . Zur Berechnung von |
Die Integration entlang der Grundseite (Riemann) entspricht gerade der Zerlegung des Parallelogramms in Rechteck und Dreiecke. | |
| Betrachte eine Parallele zur Grundseite und Integriere über die Höhe | Analog zum Rechteck. Es gilt: 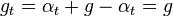 |
Die Integration entlang der Höhe (Lebesgue) entspricht der Idee, dass Scherungen Flächeninhalte nicht ändern. | |
| Mittels der Determinante bzw. Koordinatentransformation | siehe zum Beispiel hier | Die Transformation um Scherung  ist gegeben durch ist gegeben durch
|
Scherungen entsprechen Koordinatentransformationen |
Arbeitsphase (Flächeninhalt von anderen Formen)
In einem nächsten Schritt haben wir uns die Frage gestellt, wie Flächen von komplexeren Formen berechnet werden können. Eine klassische Schulbuchaufgabe ist hier beispielsweise die approximative Bestimmung der Landfläche des Südpols, mit Hilfe einer Landkarte mit geeigneten Maßstab. Dies führt zu zwei verschiedenen Herangehensweisen:
- Zerlegen und Ergänzen [Der Südpol wird einmal mit "Normrechtecken" ausgelegt]
- Benutzung von Scherungen, denn diese ändern nicht den Flächeninhalt.
Die zweite Möglichkeit verwendet dabei das Konzept von Cavalieri:
Das Prinzip von Cavalieri (für Flächen)
In einer Ebene werden zwei Figuren und die Schar aller zu einer Geraden parallelen Geraden betrachtet. Wenn für jede Gerade der Schar die beiden Schnitte mit den zwei Figuren gleich lang sind, so sind die beiden Figuren flächengleich.
Das Prinzip von Cavalieri (für Körper)
Im Raum werden zwei Körper und die Schar aller zu einer Ebene parallelen Ebenen betrachtet. Wenn für jede Ebene der Schar die beiden Schnittflächen mit den zwei Körpern gleichen Flächeninhalt haben, so sind die beiden Körper volumengleich.
Betrachtet man verschiedene Schulbücher und untersucht, wie diese die Flächenberechnung des Parallelogramms begründen, so verwenden diese eigentlich nur die Methode der Zerlegung. Eine Diskussion unter den Sitzungsteilnehmern führte in diesem Kontext zu folgenden Ergebnis:
Die Methode des Zerlegens ist sehr einsichtig. Sie kann sehr einfach von der Klasse nachvollzogen werden und es besteht somit kein Interesse an einer anderen Methode. Es ist in diesem Zusammenhang aber auch Anzumerken, dass in höheren Klassenstufen Scherungen notwendig werden, zur Bestimmung des Volumens bei Kegel, Kugel, Pyramid, etc..
Nachbereitungsauftrag
Im Jahre 1994 veröffentlichte das Journal Diabetes Care den Artikel „A Mathematical Model for the Determination of Total Area Under Glucose Tolerance and Other Metabolic Curves“ von Mary M. Tai. In dem Artikel entwickelt und validiert Tai eine Methode zur Berechnung der Fläche unter einer Blutzuckerkurve.
- Finden Sie heraus, wann und von wem die Integrationstheorie und insbesondere die Trapezregel entwickelt wurde. Lesen Sie dann Tai (1994) „A Mathematical Model for the Determination of Total Area Under Glucose Tolerance and Other Metabolic Curves“.
- Für die Validierung „ihres“ Approximationsverfahrens vergleicht Tai ihre Rechenergebnisse mit einem Bestimmungsverfahren für den „wahren Wert“. Diskutieren Sie die beiden Verfahren vor dem Hintergrund des Messen-durch-Auslegen-und-Zählen-Aspekts, des Messen-als-Berechnen-Aspekts und des Vergleichsaspekt (vgl. Grundprinzipien des Messens in ).
- Analysieren Sie die Fehler/Fehlvorstellung zum Messen, die in dem Artikel sichtbar werden. Skizzieren Sie Hypothesen, wie diese Fehlvorstellungen entstanden sein könnten und wie Sie Ihnen im Unterricht der Sekundarstufe II begegnen bzw. im Unterricht der Sekundarstufe I vorbeugen könnten.
Ergebnisse der Nachbereitung
Tragen Sie hier die Ergebnisse Ihrer Nachbereitung in Textform (nicht länger als 500 Wörter) ein.
Abgabe von pq
- Die Frage nach Flächeninhalten, hier speziell im Flächeninhalt unter einer Kurve aka Integral, ist so alt wie die Mathematik selbst. Die in der Arbeit Tai (1994) „A Mathematical Model for the Determination of Total Area Under Glucose Tolerance and Other Metabolic Curves“ angeführte Methodik des Ausfüllens oder Erschöpfens einer Fläche durch kleinere Flächen, deren Flächeninhalte durch bekannte Formeln trivial bestimmbar sind, findet sich zuerst beim antiken griechischen Philosophen Antiphon, der im 5. Jahrhundert vor Christus lebte. Dieser Methode bediente sich später auch Johannes Kepler, der bei der Berechnung von Planetenbahnen eben Integrale durch einfachere Flächen approximierte und damit die heute bekannte numerische Integration nutzte. Basierend auf dieser einfachen Idee entwickelten die Mathematiker Gottfried Wilhelm Leibniz und Sir Isaac Newton unabhängig voneinander die Theorie der Differential- und Integralrechnung, welche mithilfe der Infinitesimalrechnung die Approximation eines Integrals durch infinitesimal kleine Quader oder Trapeze erlaubt. Numerische Verfahren zur Bestimmung solcher einfacher, aber auch komplexerer, Integrale waren 1994 sicher bereits weit verbreitet.
- Zur Validierung ihres Verfahrens vergleichen Tai et al. die Ergebnisse ihrer neuartigen Methode mit einer ground truth, welche darin besteht, die Kurve auf Millimeterpapier zu zeichnen und die Kästchen unter der Kurve zu zählen (Messen-durch-Auslegen-und-Zählen-Aspekt) (The validity of each model was verified through comparison of the total area obtained from the above formulas to a standard (true value), which is obtained by plotting the curve on graph paper and counting the number of small units under the curve. The sum of these units represents the actual total area under the curve.). Dabei scheinen sie nicht zu bemerken, dass dieses Verfahren ebenso eine Approximation des gewünschten Ergebnisses ist, wenn auch eine hinreichend genaue. Beide Verfahren beinhalten also einen Prozess des Messens. Die "neu entwicklete" Methode beinhaltet über das Messen der Seiten der Trapeze hinaus jedoch einige Rechnungen und entspricht vielmehr einem berechnenden Ansatz, wie es eben auch der Fall für das Berechnen von Flächeninhalten von einfachen geometrischen Objekten der Fall ist (Messen-als-Berechnen-Aspekt). Beide Methoden werden empirisch verglichen, indem man die relativen Abweichungen der Ergebnisse in verschiedenen Tests prüft. Dabei scheint den Autoren auch nicht bewusst zu sein, dass es sich bei ihrem Vergleich nicht um einen Beweis handelt, welcher ihre Methode validiert. Beispielsweise könnten die Tests nur einen Teil von möglichen Szenarien abdecken, in welchen ihr Verfahren eben die gewünschte Genauigkeit aufweist. Schließlich werden die Abweichungen der neuen Methode von der "ground truth" als "statistisch nicht signifikant" bezeichnet (?).
- Aus dem Artikel wird klar, dass die Autoren die reine Messmethode für die genauere Methode, welche das "echte Ergebnis" liefert, halten. Ihre berechnende Methode halten sie, zu Recht, für eine Approximation. Unklar bleibt, wie die tatsächlichen Kurven der Tests aussahen und welche Annahmen über diese Kurven getroffen wurden. Wurden die Kurven beispielsweise als stückweise linear angenommen, so liefert die angewandte Trapezregel offenbar sogar das exakte Ergebnis und ist damit sogar genauer als die Messen-durch-Auslegen-und-Zählen-Methode. Das Missverständnis der Autoren scheint für mich auf der kindlichen Vorstellung zu beruhen, dass etwas, dass ich tatsächlich messe und sehe, das echte und richtige Ergebnis ist. Dagegen scheinen Tai et al. jedoch erkannt zu haben, das sie das Integral der Kurve (wenn sie denn nicht stückweise linear angenommen wird) durch die Trapeze und damit Flächen unter stückweisen linearen Kurven nur approximieren. Im Falle, dass die Trapezregel tatsächlich die exakte Lösung darstellt, bleibt diese Auffassung für mich jedoch ein Rätsel. Um solchen Vorstellungen vorzubeugen, sollte im Laufe der Sekundarstufe I stark betont werden, dass eine Messung immer mit einer Messgenauigkeit und einem Messfehler zusammenhängen. Hier könnten Beispiele und Vergleiche von Messung und Berechnung schon am Beispiel von Dreiecken herangezogen werden. Am Beispiel des Kreises lässt sich dieser Sachverhalt noch deutlicher darstellen, da sich Kreise nie vollständig durch Dreiecke oder Vierecke auslegen lassen. In der Sekundarstufe II ist es wichtig bei der Einführung des Hauptsatzes der Integral- und Differenzialrechnung darauf wert zu legen, dass die Approximation durch Ober- und Untersummen (i.e. Quader) immer genauer wird, wenn die Zerlegungsintervalle kleiner werden und nur dann exakt ist, wenn die Teile unendlich klein sind. Das analytische Integral ist also tatsächlich die einzige exakte Lösung für beliebige Kurven.
Weitere Fragen/Anmerkungen:
- Habe ich etwas falsch verstanden?
- Beispielrechnung auf Seite zwei enthält einen Klammerfehler/Typo, das Ergebnis ist jedoch korrekt.
- Wie rechtfertigt sich die Annahme, dass der Blutzuckerspiegel stückweise linear approximiert werden kann?
- Was waren die anderen Formeln zur Berechnung des Blutzuckers?
- Gab es 1994 keinen Reviewingprocess für wissenschaftliche Arbeiten?
- Was haben die Autoren dieser Arbeit im Mathematikunterricht gemacht?
- Warum wurde dieses Paper 273 mal zitiert, davon 6 Zitationen im Jahr 2019?!
Abgabe von xy
- Bereits griechische Gelehrte setzten sich mit der Flächeninhaltsbestimmung geometrischer Formen auseinander. Insbesondere der griechische Universalgelehrte Archimedes (287-212 v. Chr.) erzielte namhafte Ergebnisse im Kontext der Bestimmung von Flächeninhalten komplexerer geometrischer Strukturen (beispielsweise eine von einem Parallelbogen und einer Sekante eingerahmte Fläche). Aber erst Isaac Newton und Gottfried Wilhelm Leibnitz gelang es im 17. Jahrhundert, sich von der geometrischen Herangehensweise an die Flächeninhaltsbestimmung zu lösen und einen analytischen Zugang zu wählen. Verfahren zur numerischen Bestimmung von Flächeninhalten bzw. Integralen wurden seither vielfach verfeinert. Darunter fällt insbesondere auch die hier beschriebene Verwendung von Trapezen statt Rechtecken.
- Tais Modell unterteilt die Fläche unter der Kurve in Trapeze, deren Flächeninhalte mit geometrischen Mitteln eindeutig bestimmt werden können. Addiert man diese Flächeninhalte, so erhält man laut Tai eine deutlich genauere Näherung an den „tatsächlichen“ Flächeninhalt unter der Kurve als mit anderen Methoden. Den „wahren“ Wert bestimmt sie im Rahmen ihrer Studie, indem die Kurve auf Millimeterpapier gezeichnet wird und man anschließend die unter der Kurve befindlichen Kästchen addiert.Im Grunde kann man beide Ansätze als „Messen durch Auslegen und Zählen“ verstehen. Die allgemeine Herangehensweise legt die Fläche unter der Kurve mit einheitlich großen Kästchen aus und zählt diese zusammen. Tais Modell hingegen legt die Fläche mit Trapezen aus, welche an den Verlauf der Kurve angepasst sind und diese dabei besser approximieren. Zu bedenken ist jedoch, dass auch die Version für den „wahren“ Wert in diesem Aufsatz keine exakte Bestimmung des Flächeninhalts liefert, sondern eine Näherung an diesen (obwohl die Einheiten durch das Millimeterpapier recht klein gewählt sind). Tai fasst ihre Ergebnisse außerdem in einer Formel zusammen, welche an verschiedene Fälle angepasst werden kann („Messen als Berechnen“). Wie der Vergleichsaspekt in diesem Kontext Anwendung finden soll, ist mir nicht ganz klar. Einzig der besondere Fall, dass ein Teil der Kurve eine der Koordinatenachsen schneidet, könnte die Fähigkeit des Vergleichens notwendig machen. Tai hat diesen Fall in ihr Modell aufgenommen, im allgemeinen Fall müsste man jedoch mit Konzepten von orientierten Flächeninhalten arbeiten, falls der Kontext der Studie dies zulässt.
- Bei der Lektüre des Aufsatzes irritierte mich, dass nicht der Versuch unternommen wird, die Kurve durch eine geeignete Funktion zu approximieren und diese dann zu integrieren. Möglicherweise aber lassen die entsprechenden Studien eine solche Vorgehensweise nicht zu. Darüber hinaus ist der Umgang mit dem „wahren“ Flächeninhalt problematisch. Auch die Kästchenzähl-Variante bleibt lediglich eine Approximation, was Tai in ihrem Aufsatz nicht angemessen berücksichtigt. Den wahren Wert des Flächeninhalts durch Messen zu ermitteln, ist in diesem Fall nur mittels Approximation möglich, was für SuS der Sekundarstufe II möglicherweise schwer nachvollziehbar ist. Zu diesem Zweck wäre es beispielsweise hilfreich, mehrere Ansätze zur Berechnung von Flächeninhalten bzw. mehrere Herangehensweisen an das Integral zu bieten, einander gegenüberzustellen und gegeneinander abzuwägen.
.
Abgabe von fqt
Aufgabe 1
- Die Exhaustionsmethode ist ein antikes Verfahren zur Berechnung von Flächen, also zur Integration. [Eudoxus, ca. 370 v.Chr.]
- Anscheinend wurde die Trapezregel bereits ca. 50 v.Chr. in Babylon in Bezug zu astronomischen Fragestellungen angewandt.
Aufgabe 2
Die Methode von Tai's beruht auf der Unterteilung in kleine Rechtecke und Dreieck, also auf dem Messen-durch-Auslegen-und-Zählen-Aspekt. Auch die Vergleichsmethode zur Validierung verwendet diesen Aspekt, denn sie beruht auf dem Zählen der kleinsten Einheiten unter der Kurve des Graphen bis der wahre Wert bestimmt ist. Jedoch sind Tai's Ergebnisse auch als reine Formel anwendbar. Hier ist es also definitiv auch möglich vom 'Messen-als-Berechnen-Aspekts zu sprechen.
Aufgabe 3
Weder Tai's Methode noch die Vergleichsmethode stellen genaue Berechnungen dar. Dies wird von den Autoren jedoch nur für Tai's Methode selbst erkannt. Sie erkennen nicht, dass das Integral verschiedene Aspekte des Messens gleichzeitig darstellt (darstellen kann). Persönlich denke ich, dass eine Klasse in der Kursstufe einfach eine Stammfunktion bestimmen würde um den wahren Wert zu erhalten und nicht erneut approximieren würde. Ich frage mich auch, warum dies hier nicht gemacht wurde.
Abgabe von alf
Aufgabe 1
- < 17. Jhdt.: Flächeninhalts- und Voluminaberechnungen von interessanten Fallbeispielen durch das Messen durch Auslegen-und-Zählen, durch Vergleichen und Abschätzen und später auch durch erste Berechnungen. [‘‘Antiphon, Archimedes‘‘]
- > 17. Jhdt.: Flächeninhalts- und Voluminaberechnungen von einer gewaltigen Fülle konkreter Probleme mit Hilfe der Infinitisimalrechnung. Die heute in der numerischen Integration zugehörige keplersche Fassregel (Messen durch Auslegen-und-Zählen und durch Vergleichen) und der Fundamentalsatz der Analysis (Messen durch Berechnen) sind wichtige Errungenschaften der Zeit. [‘‘Cavalieri, Kepler, Leibnitz, Newton, L’Hospital, Bernoulli‘‘]
- > 19. Jhdt.: Angemessene Formulierung des Begriffs Volumens als Teilmenge von R^n. Entwicklung des Riemann- und Lebesgue-Integrals und der Maßtheorie (Messen durch Berechnen). [Cantor, Cauchy, Riemann, Lebesgue]
Aufgabe 2
Tai’s Prinzip: Approximieren des Flächeninhalts unter einer Kurve durch Zerlegens des Bereichs in Segmente bekannter Figuren (hauptsächlich Rechtecke und Dreiecke) mit unterschiedlich Breite (Delta x). Dieser Ansatz basiert auf dem Prinzips Messen durch Auslegen-und-Zählen und entspricht dem Aufsummieren unterschiedlich großer Sehentrapeze (Messen als Berechnen-Aspekt). Tai vergleicht sein Ergebnis mit einem „true value“, der graphisch durch Zählen von kleinen Standardflächen (auch Berechnen durch Auslegen-Zählen bzw. eine Art „Messgeräte-Aspekt“) bestmöglichst genähert wird. Durch das Vergleichen der Ergebnisse wird zusätzlich noch der Vergleichsaspekt von „Messergebnisse“ für eine Einschätzung der Approximationen benutzt. Die Aspekte sind oftmals nicht sauber voneinander zu trennen.
Aufgabe 3
Problematisch ist sicherlich der Vergleich mit dem „true value“, da dieser sich ebenso auf die gleiche Art Messmethode (Messen durch Auslegen-und-Zählen) beruht. Ebenso wird nicht erkannt, dass das Schätzen des „true value’“ nichts anderes beinhaltet als das Aufsummieren kleiner Rechtecke der gleichen Breite delta x (Untersumme). Diese Vorgehensweise wird jedoch grundsätzlich als schlechter erachtet als Tai’s Methode. Widerspruch? Außerdem wird in der ganzen Tabelle nie von der Anzahl ‘‘n‘‘ oder von der Breite/Breitenspanne der Teilfiguren in den einzelnen Formeln und auch der Einheitsflächen geredet. Die Aussagekraft des Vergleichs ist deshalb sehr zweifelhaft! Eine systematischer Eingrenzung des Wahren Werts durch bsp. Unter-und Obersummen wäre sinnvoller. So hätte auch der Referenzwert seinen Fehlerbereich.
Es sollte deshalb bei den SuS klar kommuniziert werden, dass
- Messen durch Auslegen-und-Zählen und auch durch ein Messgerät immer eine Approximation des wahren Werts darstellt und der so erhaltende Wert Messungenauigkeiten unterliegt
- Das Entscheidende bei der Genauigkeit von Messverfahren der Aspekte Auslegen-und-Zählen, Vergleichen, Messgerät im Allgemeinen (glatten Fkt.) die Feinheit des Messgeräts bzw. die Anzahl der Zerlegungen ist.
- die Güte der Approximationsmethode je nach Ausgangsfunktion beurteilt werden muss
- es mehrere Methoden gibt, um Flächeninhalte zu bestimmen, die in unterschiedlichen Situationen mehr oder weniger gut geeignet sind
- Approximationsmethoden wichtige Hilfsmittel zum Messen eines Flächeninhalts sind und nicht jede Funktion eine analytische Stammfunktion besitzt (Bsp. e^-(x^2)).
Literaturhinweise
- Greefrath et al. (2016) „Didaktik der Analysis“.
- Hoffmann (2018). „Konzeption von fachmathematischen Schnittstellenmodulen für Lehramtsstudierende am Beispiel ausgewählter Themen der höheren Analysis“. In khdm-Report (Masterarbeit).
- Kapitel 5 (Flächeninhalte in den Klassen 5 bis 10) in Krauter (2008). „Beiträge zur Methodik und Didaktik des Geometrieunterrichts in der Sekundarstufe 1 (Klassen 5 bis 10)“.
- siehe auch: übergreifende Literaturhinweise
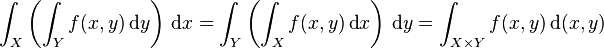

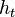 im ersten und dritten Summanden bietet sich ein Steigungsdreick zur Bestimmung von
im ersten und dritten Summanden bietet sich ein Steigungsdreick zur Bestimmung von  an.
an.

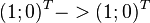 und
und