Größenbereiche: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Gewicht) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 26: | Zeile 26: | ||
==Volumina== | ==Volumina== | ||
==Geld/Preise== | ==Geld/Preise== | ||
| + | =Größen als Äquivalenzklassen= | ||
| + | Größen sind Äquivalenzklassen von Objekten: | ||
| + | |||
| + | Z.B.ist die Relation ''gleichschwer'' auf der Menge aller Körper eine Äquivalenzrelation: | ||
| + | |||
| + | # Jeder Körper ist zu sich selbst gleichschwer | ||
| + | # Wenn <math>K_1</math> gleichschwer <math>K_2</math> dann ist auch <math>K_2</math> gleichschwer <math>K_3</math> | ||
| + | # Wenn <math>K_1</math> gleichschwer <math>K_2</math> und <math>K_2</math> gleichschwer <math>K_3</math> dann <math>K_1</math> gleichschwer <math>K_3</math> | ||
| + | |||
| + | Die Größe Masse ist eine Äquivalenzklasse nach der Äquivalenzrelation gleichschwer. | ||
Version vom 10. November 2011, 23:35 Uhr
Inhaltsverzeichnis |
Beispiele
Masse
Wir betrachten physikalische Körper. Jeder Körper hat die Eigenschaft einer Krafteinwirkung Widerstand entgegenzusetzen. Man nennt diese Eigenschaft die träge Masse.
Alle Körper ziehen sich aufgrund ihrer Masse an. Diese Eigenschaft der Körper einander anzuziehen nennt man schwere Masse.
Schwere und träge Masse sind auf das engste miteinander verbunden. Besonders schwere Körper (Körper die andere besonders stark anziehen) sind auch besonders träge.
Die Masse eines Körpers wird dadurch bestimmt, dass man den Körper mit anderen Körpern vergleicht:
[ www.ph-heidelberg.de is not an authorized iframe site ]
Letztlich definieren wir auf der Menge 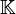 aller Körper eine Relation gleich schwer:
aller Körper eine Relation gleich schwer:
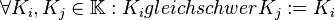 und
und 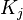 halten sich auf der Waage das Gleichgewicht.
halten sich auf der Waage das Gleichgewicht.
Gewicht
Auf jeden Körper wirkt die Anziehungskraft der Erde. Dies Kraft wird auch Gewichtskraft bzw Gewicht des Körpers genannt. Das Gewicht wird mit einem Federkraftmesser bestimmt. Auf der Menge aller Körper definieren wir: Zwei Körper haben dasselbe Gewicht, wenn sie auf den Federkraftmesser dieselbe Wirkung haben.
Längen
Flächeninhalte
Volumina
Geld/Preise
Größen als Äquivalenzklassen
Größen sind Äquivalenzklassen von Objekten:
Z.B.ist die Relation gleichschwer auf der Menge aller Körper eine Äquivalenzrelation:
- Jeder Körper ist zu sich selbst gleichschwer
- Wenn
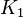 gleichschwer
gleichschwer 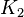 dann ist auch
dann ist auch 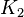 gleichschwer
gleichschwer 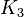
- Wenn
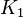 gleichschwer
gleichschwer 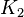 und
und 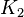 gleichschwer
gleichschwer 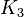 dann
dann 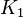 gleichschwer
gleichschwer 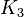
Die Größe Masse ist eine Äquivalenzklasse nach der Äquivalenzrelation gleichschwer.

