Lösung von Aufg. 12.4: Unterschied zwischen den Versionen
| Zeile 9: | Zeile 9: | ||
3) Durch zwei Punkte A und P geht genau eine Gerade_____________I/1, 1) und 2)<br /> | 3) Durch zwei Punkte A und P geht genau eine Gerade_____________I/1, 1) und 2)<br /> | ||
4) An PA+ trägt man in der Halbebene PA,B+ einen Winkel der Größe____________Winkelkonstruktionsaxiom<br /> | 4) An PA+ trägt man in der Halbebene PA,B+ einen Winkel der Größe____________Winkelkonstruktionsaxiom<br /> | ||
| − | + | |<math>\angle {PAB}</math>| an.<br /> | |
5) Der nicht auf AP liegende Schenkel des ungetragenen Winkels bestimmt eine Gerade, die man h nennt._____4)<br /> | 5) Der nicht auf AP liegende Schenkel des ungetragenen Winkels bestimmt eine Gerade, die man h nennt._____4)<br /> | ||
6) h//g__________________nach der Umkehrung des Stufenwinkelsatzes--[[Benutzer:Engel82|Engel82]] 19:54, 19. Jan. 2011 (UTC) | 6) h//g__________________nach der Umkehrung des Stufenwinkelsatzes--[[Benutzer:Engel82|Engel82]] 19:54, 19. Jan. 2011 (UTC) | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Version vom 19. Januar 2011, 21:55 Uhr
Aufgabe 12.4
Beweisen Sie: Wenn  ein Punkt außerhalb der Geraden
ein Punkt außerhalb der Geraden  ist, dann gibt es eine Gerade
ist, dann gibt es eine Gerade  , die durch
, die durch  geht und parellel zu
geht und parellel zu  ist.
ist.
Vor: g, P: P kein Element der Geraden g ist
Beh: es existiert eine Gerade h, 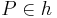 , g//h
, g//h
1) Es existieren zwei Punkte A und B, die auf der Geraden g liegen____________Axiom I/1
2)Der Punkt P liegt nicht auf der Geraden__________________________Vor.
3) Durch zwei Punkte A und P geht genau eine Gerade_____________I/1, 1) und 2)
4) An PA+ trägt man in der Halbebene PA,B+ einen Winkel der Größe____________Winkelkonstruktionsaxiom
|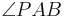 | an.
| an.
5) Der nicht auf AP liegende Schenkel des ungetragenen Winkels bestimmt eine Gerade, die man h nennt._____4)
6) h//g__________________nach der Umkehrung des Stufenwinkelsatzes--Engel82 19:54, 19. Jan. 2011 (UTC)

