Lösung von Aufgabe 14.4
Inhaltsverzeichnis |
Aufgabenstellung 1
Der Begriff des Drachen sei wie folgt definiert: Unter einem Drachen versteht man ein konvexes Viereck mit zwei Paaren benachbarter Seiten, die kongruent zueinander sind.
Man beweise: Wenn ein Viereck  ein Drachen ist, dann halbiert eine Diagonale dieses Vierecks die andere Diagonale von
ein Drachen ist, dann halbiert eine Diagonale dieses Vierecks die andere Diagonale von  .
.
Voraussetzung
- Viereck

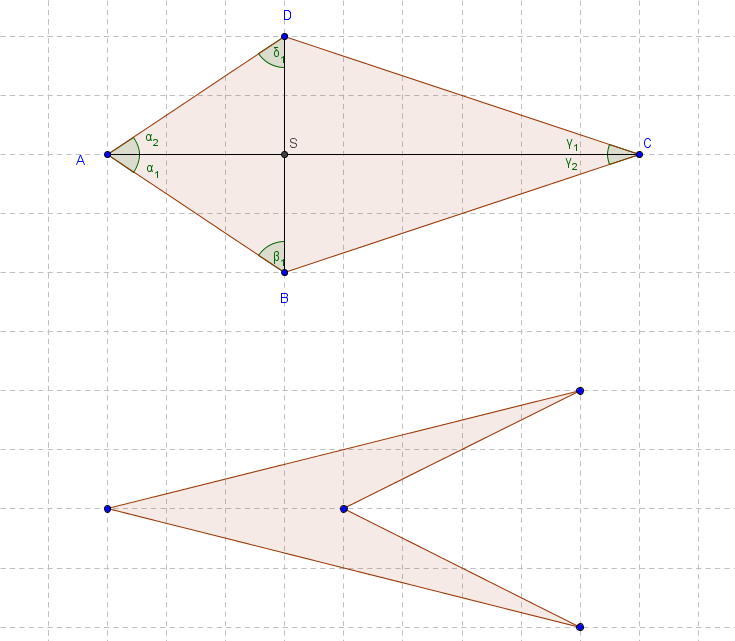
- Es gilt wie bei Fall 1 (Skizze):
 ist konvex.
ist konvex.
- Der Beweis von Fall 2 - ein konkaver Drachen: Pfeilviereck - verläuft analog, oder zumindest ähnlich.
- Es gilt (oBdA):
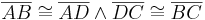
- nach Skizze:
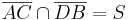
- An sich müsste bewiesen werden, dass
 und
und 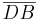 sich schneiden. Hier ein Verweis auf "Geschichten aus dem Inneren", bzw. die einfache Begründung, dass
sich schneiden. Hier ein Verweis auf "Geschichten aus dem Inneren", bzw. die einfache Begründung, dass 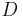 und
und  in unterschiedlichen Halbebenen bezüglich zur Geraden
in unterschiedlichen Halbebenen bezüglich zur Geraden 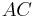 liegen.
liegen.
- An sich müsste bewiesen werden, dass
Behauptung
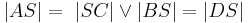
- Erklärung zu dieser Behauptung: wenn
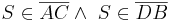 (laut VSS) und die Endpunkte EINER Diagonalen (der Diagonalen-Strecke) zu S den selben Abstand hat, so wird die eine Diagonale von der anderen halbiert.
(laut VSS) und die Endpunkte EINER Diagonalen (der Diagonalen-Strecke) zu S den selben Abstand hat, so wird die eine Diagonale von der anderen halbiert.
- Erklärung zu dieser Behauptung: wenn
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 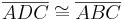
|
Dreieckskongruenz durch SSS
|
| (II) | 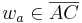 ( (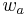 ist Winkelhalbierende des Winkels ist Winkelhalbierende des Winkels 
|
(I), Dreieckskongruenz: 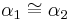
|
| (III) | 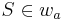
|
(II), 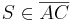 (VSS) (VSS)
|
| (IV) | 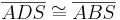
|
Dreieckskongruenz durch SWS
|
| (V) | 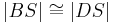
|
(IV) |
Die Diagonale 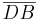 wird durch die Diagonale
wird durch die Diagonale 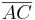 halbiert!
halbiert!
Zusatz-Aufgabe
Versuch 1
Voraussetzung: Strecke AD kongrent zu Strecke DC und Strecke AB kongruent zu Strecke BC
Behauptung: Strecke DB halbiert die Strecke AC
Beweis:
Betrachte die Mittelsenkrechte von AC. Laut MiSe-Kriterium enthält diese alle Punkte, die zu den beiden Endpunkten A und C
jeweils denselben Abstand haben.
Laut Voraussetzung gilt, dass D denselben Abstand zu A und C hat, ferner hat B denselben Abstand
zu A und C. Wegen dem o.g. Kriterium gehören nun D und B zu der Mittelsenkrechte der Strecke AC. Da ABCD nicht konvex, und wegen Definition Mittelsenkrechte folgt nun, dass die Strecke DB die Strecke AC halbiert.
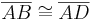 nach VSS
nach VSS
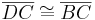 nach VSS
nach VSS
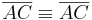 trivial
trivial
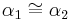 (I)
(I)
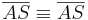 trivial
trivial

