Lösung von Aufgabe 3.1 S (SoSe 12): Unterschied zwischen den Versionen
(→Lösungsvorschlag 9:) |
(→Lösungsvorschlag 9:) |
||
| Zeile 69: | Zeile 69: | ||
=== Lösungsvorschlag 9: === | === Lösungsvorschlag 9: === | ||
Wenn eine Strecke <math>\overline {AB}</math> im Mittelpunkt M der Strecke <math>\overline {AB}</math> von einer Geraden CD senkrecht geschnitten wird, dann ist CD die Mittelsenkrechte von <math>\overline {AB}</math>.--[[Benutzer:Kopernikus|Kopernikus]] 19:58, 9. Mai 2012 (CEST)<br /> | Wenn eine Strecke <math>\overline {AB}</math> im Mittelpunkt M der Strecke <math>\overline {AB}</math> von einer Geraden CD senkrecht geschnitten wird, dann ist CD die Mittelsenkrechte von <math>\overline {AB}</math>.--[[Benutzer:Kopernikus|Kopernikus]] 19:58, 9. Mai 2012 (CEST)<br /> | ||
| + | |||
| + | |||
| + | ==== Verbesserungen ==== | ||
| + | Ich habe bei einigen Def. ein paar Dinge verändert. Mir ist besonders aufgefallen, dass oft der "Bezug" vergessen wurde. Also z.B. | ||
| + | *Wenn eine Gerade durch den Mittelpunkt einer Strecke <math>\overline {AB}</math> verläuft, dann ist sie Mittelsenkrechte. | ||
| + | Es müsste aber heißen: | ||
| + | *Wenn eine Gerade durch den Mittelpunkt einer Strecke <math>\overline {AB}</math> verläuft, dann ist sie Mittelsenkrechte der Strecke <math>\overline {AB}</math>.--[[Benutzer:Andreas|Tutor Andreas]] 13:05, 22. Mai 2012 (CEST) | ||
Version vom 22. Mai 2012, 13:05 Uhr
Inhaltsverzeichnis |
Aufgabe 3.1
Unter einer Konventionaldefinition versteht man eine Definition, die in der Form "Wenn-Dann" formuliert wurde.
Geben Sie zwei prinzipiell verschiedene Konventionaldefinitionen des Begriffs Mittelsenkrechte einer Strecke an.
Wenn eine Gerade g senkrecht auf einer Strecke  steht und durch den Mittelpunkt der Strecke
steht und durch den Mittelpunkt der Strecke  verläuft, dann ist g Mittelsenkrechte.--Oz44oz 21:53, 1. Mai 2012 (CEST)
verläuft, dann ist g Mittelsenkrechte.--Oz44oz 21:53, 1. Mai 2012 (CEST)
Lösungsvorschlag 2:
Wenn eine Gerade eine Mittelsenkrechte ist, dann halbiert sie eine Strecke  und steht dabei senkrecht auf ihr.
und steht dabei senkrecht auf ihr.
Da hier ja nach zwei prinzipiell verchiedenen Konventionaldefinitionen gefragt ist. Meine Frage: Könnte man auch folgendes sagen?????
Wenn eine Gerade eine Mittelsenkrechte ist, dann ist sie die Menge aller Punkte, die von zwei Punkten A und B den gleichen Abstand hat.
Ansonsten fallen mir nämlich nurnoch ähnliche Forumlierungen wie oben ein.--Goliath 17:42, 3. Mai 2012 (CEST)
Ich habe auch so eine Definition, die in deine Richtung geht bzw. gleiches sagt^^ :"Wenn eine Menge M nur alle Punkte beinhaltet, die gleichweit von zwei verschiedenen Punkten (nicht Element M) entfernt sind, dann nennt man diese Menge Mittelsenkrechte." --RitterSport 20:54, 6. Mai 2012 (CEST)
@Goliath Sie wollen den Begriff Mittelsenkrechte definieren. Müsste das nicht eher in der folgenden Form passieren: Wenn Bedingungen, dann ist das Objekt eine Mittelsenkrechte. Kann man den zu definierenden Begriff in der Voraussetzung verwenden? s. Kommentar zu Hauleri unten.--*m.g.* 17:51, 6. Mai 2012 (CEST)
@ M.G. Ich bin gerade ein wenig irritiert. Ich hatte das letzte Woche bei Aufgabe 2.6 so gemacht. Bsp.: Ich hatte geschrieben: "Wenn ein Viereck  vier rechte Innenwinkel hat, dann ist es ein Quadrat."
Dann hieß es in der Übung, dass das falsch sei. Das es so heißen müsste: "Wenn
vier rechte Innenwinkel hat, dann ist es ein Quadrat."
Dann hieß es in der Übung, dass das falsch sei. Das es so heißen müsste: "Wenn  ein Quadrat ist, dann hat es vier rechte Innenwinkel."
Da waren einige etwas verwirrt, weil keiner mehr wusste, was jetzt nach vorne kommt und was nicht.HILFE - bin total verwirrt!!!!!!
ein Quadrat ist, dann hat es vier rechte Innenwinkel."
Da waren einige etwas verwirrt, weil keiner mehr wusste, was jetzt nach vorne kommt und was nicht.HILFE - bin total verwirrt!!!!!!
Oder liegt das daran, dass es in Aufgabe 2.6 darum ging, eine gegebene Implikation in die Wenn-Dann Form zu bringen. Da ja mein Beispiel nicht eindeutig ein Quadrat bestimmt. Ich hoffe man versteht, was ich meine.
Wäre es dann so richtig:
- Wenn eine Gerade eine Strecke halbiert und dabei senkrecht auf ihr steht, dann ist es eine Mittelsenkrechte.
- Wenn eine Gerade die Menge aller Punkte ist, die von zwei Punkten A und B den gleichen Abstand haben, dann ist sie eine Mittelsenkrechte.--Goliath 17:52, 7. Mai 2012 (CEST)
Lösungsvorschlag 3:
Wenn eine Mittelsenkrechte auf die Strecke  trifft, dann sind die beiden Nebenwinkel rechte Winkel.
trifft, dann sind die beiden Nebenwinkel rechte Winkel.
Wenn eine Mittelsenkrechte die Strecke  schneidet, dann ist der Schnittpunkt der Mittelpunkt M der Geraden
schneidet, dann ist der Schnittpunkt der Mittelpunkt M der Geraden  . --Hauleri 13:10, 6. Mai 2012 (CEST)
. --Hauleri 13:10, 6. Mai 2012 (CEST)
Aber im zweiten Vorschlag könnte es doch auch sein, dass die Mittelsenkrechte die Strecke in jedem beliebigen Winkel schneidet, oder?
Kommentar M.G.
@Hauleri Sie wollen den Begriff Mittelsenkrechte in Wenn-Dann-Form definieren. Ich bring hier mal ein paar andere Konventionaldefinitionen:
Definition
Teiler
Es seien t und  zwei ganze Zahlen. Wenn es eine ganze Zahl
zwei ganze Zahlen. Wenn es eine ganze Zahl  derart gibt, dass
derart gibt, dass 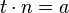 gilt, dann ist
gilt, dann ist  ein Teiler von
ein Teiler von  .
.
Definition
Sehnenviereck
Wenn ein Viereck einen Umkreis hat, dann ist es ein Sehnenviereck.
Definition
Raute
Wenn in einem Viereck alle Seiten zueinander kongruent sind, dann heißt das Viereck Raute.
Schaun Sie einfach mal nur nach der Syntax. Wo steht immer der zu zu definierende Begriff?--*m.g.* 17:47, 6. Mai 2012 (CEST)
Lösungsvorschlag 4:
Wenn zu einer Strecke  eine Gerade orthogonal durch den Mittelpunkt der Strecke
eine Gerade orthogonal durch den Mittelpunkt der Strecke  verläuft, dann ist diese Gerade die Mittelsenkrecht (oder das Mittellot) von
verläuft, dann ist diese Gerade die Mittelsenkrecht (oder das Mittellot) von  .
.
Lösungsvorschlag 5:
Es sei  eine Strecke, die durch eine Gerade g orthogonal im Punkt M geschnitten wird. Ist AM = MB, dann ist g die Mittelsenkrechte der Strecke
eine Strecke, die durch eine Gerade g orthogonal im Punkt M geschnitten wird. Ist AM = MB, dann ist g die Mittelsenkrechte der Strecke  .--KeinKurpfälzer 19:56, 6. Mai 2012 (CEST)
.--KeinKurpfälzer 19:56, 6. Mai 2012 (CEST)
==== Zu Lösungsvorschlag 4 und 5 ====
Orthogonal...ich finds schön....aber ich denke, dass man es vorher noch def. müsste, bevor man es verwendet.--Kopernikus 19:58, 9. Mai 2012 (CEST)
Lösungsvorschlag 6:
Wenn eine Gerade senkrecht durch den Mittelpunkt M einer Strecke  geht, dann ist diese Gerade eine Mittelsenkrechte --Mahe84 11:50, 8. Mai 2012 (CEST)
geht, dann ist diese Gerade eine Mittelsenkrechte --Mahe84 11:50, 8. Mai 2012 (CEST)
Lösungsvorschlag 7:`
Wenn eine Gerade die Menge aller Punkte ist, die den gleichen Abstand zu zwei gegeben voneinander versch. Punkten A,B hat, dann ist diese Gerade die Mittelsenkrechte der Strecke  --Mahe84 11:50, 8. Mai 2012 (CEST)
--Mahe84 11:50, 8. Mai 2012 (CEST)
Lösungsvorschlag 8:
Gegeben sei eine Strecke  und eine Punktmenge P. Wenn alle Elemente der Punktmenge P jeweils ein und den selben Abstand zu den beiden Endpunkten der Strecke
und eine Punktmenge P. Wenn alle Elemente der Punktmenge P jeweils ein und den selben Abstand zu den beiden Endpunkten der Strecke  besitzen, dann ist die Punktmenge P die Mittelsenkrechte der Strecke
besitzen, dann ist die Punktmenge P die Mittelsenkrechte der Strecke  . --Jama77 23:30, 8. Mai 2012 (CEST)
. --Jama77 23:30, 8. Mai 2012 (CEST)
Lösungsvorschlag 9:
Wenn eine Strecke  im Mittelpunkt M der Strecke
im Mittelpunkt M der Strecke  von einer Geraden CD senkrecht geschnitten wird, dann ist CD die Mittelsenkrechte von
von einer Geraden CD senkrecht geschnitten wird, dann ist CD die Mittelsenkrechte von  .--Kopernikus 19:58, 9. Mai 2012 (CEST)
.--Kopernikus 19:58, 9. Mai 2012 (CEST)
Verbesserungen
Ich habe bei einigen Def. ein paar Dinge verändert. Mir ist besonders aufgefallen, dass oft der "Bezug" vergessen wurde. Also z.B.
- Wenn eine Gerade durch den Mittelpunkt einer Strecke
 verläuft, dann ist sie Mittelsenkrechte.
verläuft, dann ist sie Mittelsenkrechte.
Es müsste aber heißen:
- Wenn eine Gerade durch den Mittelpunkt einer Strecke
 verläuft, dann ist sie Mittelsenkrechte der Strecke
verläuft, dann ist sie Mittelsenkrechte der Strecke  .--Tutor Andreas 13:05, 22. Mai 2012 (CEST)
.--Tutor Andreas 13:05, 22. Mai 2012 (CEST)

