Lösung von Aufgabe 9.1P (SoSe 12)
Beweisen Sie die Halbgeradentreue der Geradenspiegelung. Nutzen Sie für den Beweis die Streckentreue der Geradenspiegelung und eine geeignete Definition des Begriffs Halbgerade.
Manchmal kommt man nicht weiter, weil man nicht weiß wie es losgehen soll. Deshalb fange ich hier mal an. Diese Struktur kann auch für die anderen Aufgaben genutzt werden.(z.B. kopieren, um die Formelschreibweise auf einer anderen Seite zu nutzen)--Tutorin Anne 13:03, 21. Jun. 2012 (CEST)
| Voraussetzung | Geradenspiegelung an g 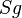 mit mit 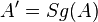 und und 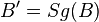 und und 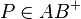
|
| Behauptung | 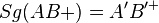 d.h. d.h. 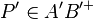
|
Es muss also gezeigt werden, dass das Bild 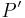 eines beliebigen Punkts
eines beliebigen Punkts  der Halbgerade auch auf dem Bilder der Halbgeraden liegt.
der Halbgerade auch auf dem Bilder der Halbgeraden liegt.
| Beweisschritt | Begründung |
|---|---|
1 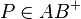 |
(Begründung 1) |
| 2 (Schritt 2) | (Begründung 2) |
| 3 (Schritt) | (Begründung) |
| 4 (Schritt) | (Begründung) |
Mal ein Versuch:
| Beweisschritt | Begründung |
|---|---|
1 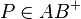 |
Voraussetzung |
2 Zw(ABP)  Zw (APB) Zw (APB) |
(1), Def. Zw., Def. Halbgerade |
3 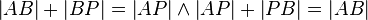 |
(2), Def. koll |
4 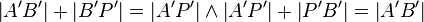 |
(3), Abstandserhaltung der Geradenspiegelung |
5 Zw(A'B'P')  Zw(A'P'B') Zw(A'P'B') |
(4), Def. Zw |
6 P A'B'+ A'B'+ |
(5) |
--Zitrone 12:50, 24. Jun. 2012 (CEST)
Habe das etwas anders gemacht und zwar bin ich gleich am Anfang auf die Definition Halbgerade AB+ und dann auf die Spiegelung von A und B eingegangen und habe dann die Definition der Halbgerade A´B´+ erstellt. Dadurch wäre es dann klar, das P´ A´B´+ ist.
Geht das so auch? --PippiLotta 13:48, 25. Jun. 2012 (CEST)
A´B´+ ist.
Geht das so auch? --PippiLotta 13:48, 25. Jun. 2012 (CEST)
Ich habe es so gemacht:
Ich muss zeigen, dass P Element von A´B`+ ist. Zuerst habe ich AB+ definiert AB+: {P für die gilt: Zw(ABP)} und {P für die gilt: Zw (APB)} und {A,B}.
Wir hätten dann vier Fälle:
1) P=A
2) P=B
3) Zw(APB)
4) Zw (ABP)
1), 2) und 3) haben wir schon bewiesen: Streckentreue (aber ich denke, es ist wichtig ist, entweder die drei Beweise zu führen, oder sich auf die Streckentreue zu berufen!) Bleibt also noch der Beweis zu 4), der geht dann ähnlich dem von 3). --Honeydukes 14:35, 25. Jun. 2012 (CEST)

