Probeklausur WS 12 13 Aufgabe 2: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe d) |
||
| Zeile 32: | Zeile 32: | ||
=Aufgabe d= | =Aufgabe d= | ||
Es sei <math>\overline{ABC}</math> ein Dreieck mit den schulüblichen Bezeichnungen. Es sei bereits gezeigt:<math> |a|>|b| \Rightarrow |\alpha| > |\beta|</math>. Beweisen Sie in der absoluten Geometrie:<math> |\alpha|>|\beta| \Rightarrow |a| > |b|</math>. | Es sei <math>\overline{ABC}</math> ein Dreieck mit den schulüblichen Bezeichnungen. Es sei bereits gezeigt:<math> |a|>|b| \Rightarrow |\alpha| > |\beta|</math>. Beweisen Sie in der absoluten Geometrie:<math> |\alpha|>|\beta| \Rightarrow |a| > |b|</math>. | ||
| + | |||
| + | |||
| + | |||
| + | ==Lösung User ...== | ||
| + | |||
| + | |||
| + | ==Lösung User ...== | ||
| + | |||
| + | |||
| + | =Aufgabe e= | ||
| + | Es gelte: <math>|AB|=\frac{1}{3}, |BC|=\frac{1}{4}, |AC|=0,9</math>. Existiert <math>\overline{ABC}</math>? Begründen Sie Ihre Antwort. | ||
| + | |||
| + | |||
| + | ==Lösung User ...== | ||
| + | |||
| + | |||
| + | ==Lösung User ...== | ||
Version vom 3. Februar 2013, 19:18 Uhr
Inhaltsverzeichnis |
Aufgabe a
Begründen Sie kurz und knapp, warum im gleichseitigen Dreieck alle Winkel zueinander kongruent sind.
Lösung User ...
Lösung User ...
Aufgabe b
Welcher Satz ist unabdingbar für den Beweis der Eindeutigkeit des Lotes von einem Punkt auf eine Gerade im Rahmen der absoluten Geometrie?
Lösung User ...
Lösung User ...
Aufgabe c
Bezüglich eines kartesischen Koordinatensystems mit dem Ursprung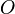 
sei ein Einheitskreis 
in Mittelpunktslage gegeben. Ferner seien 
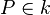und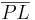 
das Lot von 
auf die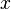 
-Achse. Beweisen Sie unter Bezug auf eine Skizze in der Euklidischen Geometrie: Wenn 
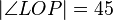° dann ist 
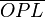gleichschenklig.
Lösung User ...
Lösung User ...
Aufgabe d
Es sei 
ein Dreieck mit den schulüblichen Bezeichnungen. Es sei bereits gezeigt: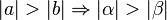
. Beweisen Sie in der absoluten Geometrie:
.
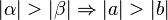Lösung User ...
Lösung User ...
Aufgabe e
Es gelte: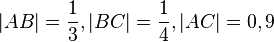 
. Existiert ? Begründen Sie Ihre Antwort.
