|
 |
|
| Abbildung 02 |
Abbildungs 03
|
Aufgabe a
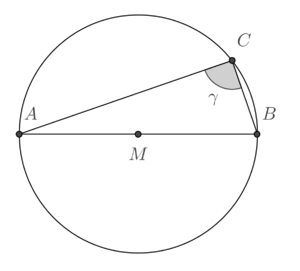
Es sei  ein Kreis mit dem Mittelpunkt ein Kreis mit dem Mittelpunkt  , auf , auf  seien drei nichtkollineare Punkte seien drei nichtkollineare Punkte  gegeben. gegeben.
Voraussetzung 1: 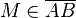 , ,
Voraussetzung 2: 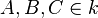 , ,
Behauptung 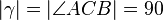 ° °
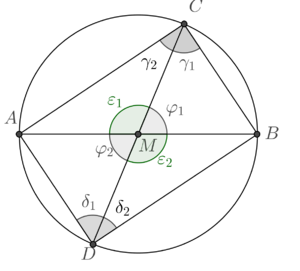
Für den folgenden Beweis beziehen wir uns auf Abb. 03. Hier wurde der Durchmesser  eingezeichnet und zum Viereck eingezeichnet und zum Viereck  ergänzt. Die Korrektheit dieser Konstruktion muss nicht begründet werden. Ergänzen Sie das folgende Beweisfragment: ergänzt. Die Korrektheit dieser Konstruktion muss nicht begründet werden. Ergänzen Sie das folgende Beweisfragment:
Lösung ...lw)...
| Nr. |
Beweisschritt |
Begründung
|
| (I) |
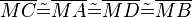 |
...Vor., Definition Abstand eines Punktes von k zu M (Radius eines Kreises)
|
| (II) |
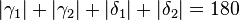 ° ° |
...Vor., Sehnenviereckskriterium (?)oder Basiswinkelsatz und Rechnen in R (?)
|
| (III) |
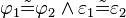 |
... Vor., Def. Scheitelwinkel, (I), SWS
|
| (IV) |
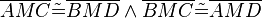 |
... (III), Def. Dreieckskongruenz
|
| (V) |
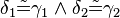 |
... (IV), (II), Rechnen in R
|
| (VI) |
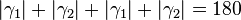 ° ° |
... (V), Rechnen in R
|
| (VIII) |
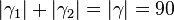 ° ° |
... (VI), Rechnen in R
|
| (VII) |
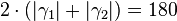 ° ° |
...
|
Ist so nicht korrekt Orientieren Sie sich an der Lösung von ----B hier drunter. --*m.g.* 13:32, 9. Feb. 2013 (CET)
Lösung User ...--B..... 14:46, 5. Feb. 2013 (CET)
| Nr. |
Beweisschritt |
Begründung
|
| (I) |
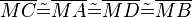 |
... Vor.2, Def. Sehnenviereck
|
| (II) |
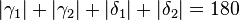 ° ° |
...1), Sehnenvierecksktriterium
|
| (III) |
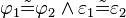 |
... kongruente Scheitelwinkel, Def. Scheitelwinkel
|
| (IV) |
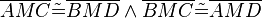 |
...1), 3), Kongruenzaxiom SWS
|
| (V) |
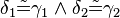 |
...4), Def. Dreieckskongruenz
|
| (VI) |
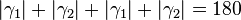 ° ° |
... 2),5)
|
| (VIII) |
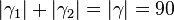 ° ° |
...6), rechnen in R
|
| (VII) |
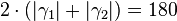 ° ° |
... 7), rechen in R
|
passt, rechnen in R wäre nicht extra nötig gewesen, ist aber natürlich auch nicht falsch.--*m.g.* 13:37, 9. Feb. 2013 (CET)
Aufgabe b
Formulieren Sie den unter a) bewiesenen Satz in allgemeinerer Form unter Verwendung der Begriffe Dreieck und Umkreis in der Form Wenn-Dann.
Lösung User ...lw)...
Wenn ein alle drei Punkte A,B,C eines Dreiecks auf dessen Umkreis k liegen und die Basis  ein Druchmesser von k ist, dann ist das Dreieck ein rechtwinkliges Dreieck. --...lw)... 11:06, 5. Feb. 2013 (CET) ein Druchmesser von k ist, dann ist das Dreieck ein rechtwinkliges Dreieck. --...lw)... 11:06, 5. Feb. 2013 (CET)
geht so leider gar nicht--*m.g.* 14:19, 5. Feb. 2013 (CET)
Lösung User ...--B..... 14:48, 5. Feb. 2013 (CET)
Wenn bei einem Dreieck ABC mit dem Umkreis k, der Mittelpunkt M, von dem Kreis k, Teil der Srecke AB ist, dann ist der Winkel ACB = 90.--B..... 14:48, 5. Feb. 2013 (CET)
Lösung User anika1
Wenn alle drei Punkte A,B,C eines Dreicks auf dessen Umkreis liegen und die Basis  ein Durchmesser von k ist, dann ist jeder Peripheriewinkel von k über ein Durchmesser von k ist, dann ist jeder Peripheriewinkel von k über  ein rechter Winkel. --Anika1 12:58, 9. Feb. 2013 (CET) ein rechter Winkel. --Anika1 12:58, 9. Feb. 2013 (CET)
Bemerkung --*m.g.* 13:36, 9. Feb. 2013 (CET)
Was haben die Peripheriewinkel mit dem Dreieck zu tun? Was hat der Umkreis des Dreiecks mit dem Kreis k zu tun? Sie unterstellen sicherlich, dass es ein und derselbe Kreis sein soll, nur kann Ihr Text auch anders interpretiert werden.
Versuchen Sie es wie folgt: Wenn der Mittelpunkt des Umkreises eines Dreiecks auf einer Seite dieses ..............., dann ist das Dreick ein ......, wobei der rechte Winkel der Seite ........
--*m.g.* 13:36, 9. Feb. 2013 (CET)
|


 ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  , auf
, auf  gegeben.
gegeben. 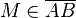 ,
,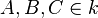 ,
, 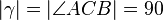 °
°  eingezeichnet und zum Viereck
eingezeichnet und zum Viereck  ergänzt. Die Korrektheit dieser Konstruktion muss nicht begründet werden. Ergänzen Sie das folgende Beweisfragment:
ergänzt. Die Korrektheit dieser Konstruktion muss nicht begründet werden. Ergänzen Sie das folgende Beweisfragment:
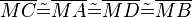
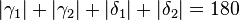 °
° 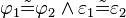
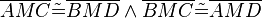
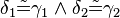
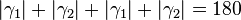 °
° 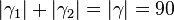 °
° 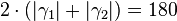 °
°  ein Druchmesser von k ist, dann ist das Dreieck ein rechtwinkliges Dreieck. --
ein Druchmesser von k ist, dann ist das Dreieck ein rechtwinkliges Dreieck. --
