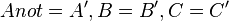Reduktionssatz: Jede Bewegung ist die NAF von zwei oder drei Geradenspiegelungen: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „==Drei nicht kollineare Punkte reichen aus== ===Satz:=== ::Jede Bewegung ist durch drei nicht kollineare Punkte und deren Bilder eindeutig bestimmt. ==Der Redukt…“)
 
(→‎Beweis)
Zeile 8: Zeile 8:
 
Es seien <math>A, B, C</math> drei nicht kollineare Punkte und <math>\varphi</math> eine Bewegung.<br />
 
Es seien <math>A, B, C</math> drei nicht kollineare Punkte und <math>\varphi</math> eine Bewegung.<br />
 
<math>A'=\varphi(A), B'=\varphi(B), C'=\varphi(C)</math> seien die Bilder von <math>A, B, C</math> bei <math>\varphi</math>
 
<math>A'=\varphi(A), B'=\varphi(B), C'=\varphi(C)</math> seien die Bilder von <math>A, B, C</math> bei <math>\varphi</math>
 +
====Fall 1====
 +
<math>A=A', B=B', C=C'</math>
 +
====Fall 2====
 +
o.B.d.A.
 +
<math>A=A', B=B'</math>
 +
====Fall 3====
 +
o.B.d.A.
 +
<math>A=A'</math>
 +
====Fall 4====
 +
<math>Anot=A', B=B', C=C'</math>

Version vom 22. November 2011, 07:10 Uhr

Inhaltsverzeichnis

Drei nicht kollineare Punkte reichen aus

Satz:

Jede Bewegung ist durch drei nicht kollineare Punkte und deren Bilder eindeutig bestimmt.

Der Reduktionssatz

Satz: Reduktionssatz

Jede Bewegung ist die Nacheinanderausführung von zwei oder drei Geradenspiegelungen.

Beweis

Es seien A, B, C drei nicht kollineare Punkte und \varphi eine Bewegung.
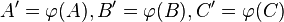A'=\varphi(A), B'=\varphi(B), C'=\varphi(C) seien die Bilder von A, B, C bei \varphi

Fall 1

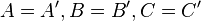
A=A', B=B', C=C'

Fall 2

o.B.d.A. A=A', B=B'

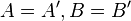
Fall 3

o.B.d.A. A=A'

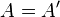
Fall 4

Anot=A', B=B', C=C'

Von „http://geometrie.zum.de/index.php?title=Reduktionssatz:_Jede_Bewegung_ist_die_NAF_von_zwei_oder_drei_Geradenspiegelungen&oldid=9558“