Schubspiegelung (2011/12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „==Die Idee== Entsprechend der Bezeichnung ''Schubspiegelung'' würde man unter einer Schubspiegelung dir Nacheinanderausführung Einer Verschiebung mit einer Gera…“) |
*m.g.* (Diskussion | Beiträge) (→Satz) |
||
| Zeile 6: | Zeile 6: | ||
===Spiegelschiebung?=== | ===Spiegelschiebung?=== | ||
Entsprechend obiger Definition ist die NAF einer Geradenspiegelung und einer Verschiebung kommutativ,falls sie den Bedingungen der Definition ''Schubspiegelung'' genügen. | Entsprechend obiger Definition ist die NAF einer Geradenspiegelung und einer Verschiebung kommutativ,falls sie den Bedingungen der Definition ''Schubspiegelung'' genügen. | ||
| − | ==== Satz ==== | + | ==== Satz SCH/1==== |
:::Es sei <math>S_g \circ V</math> eine Schubspieglung. Dann gilt <math>S_g \circ V = V \circ S_g</math> | :::Es sei <math>S_g \circ V</math> eine Schubspieglung. Dann gilt <math>S_g \circ V = V \circ S_g</math> | ||
| + | ==== Beweis ==== | ||
| + | :::Es sei <math>S_g \circ V = S_g \circ \left(S_b \circ S_a\right)</math> | ||
{{#ev:youtube|j4T7D4cMN2U}} | {{#ev:youtube|j4T7D4cMN2U}} | ||
[[Kategorie:Elementargeometrie]] | [[Kategorie:Elementargeometrie]] | ||
Version vom 13. Dezember 2011, 13:25 Uhr
Inhaltsverzeichnis |
Die Idee
Entsprechend der Bezeichnung Schubspiegelung würde man unter einer Schubspiegelung dir Nacheinanderausführung Einer Verschiebung mit einer Geradenspiegelung verstehen. Diese Idee ist auch exakt das, was man unter einer Scubspieglung versteht. Trotzdem sie die Definition wie eine Einschränkung dieser Vorstellung aus.
Die Definition
Definition: (Schubspiegelung)
- Es sei
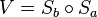eine Geradenspiegelung und 
eine Gerade, die senkrecht auf den Spiegelachsen 
und 
steht. Die NAF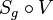 
heißt Schubspiegelung mit der Schubspiegelachse .
- Es sei
Spiegelschiebung?
Entsprechend obiger Definition ist die NAF einer Geradenspiegelung und einer Verschiebung kommutativ,falls sie den Bedingungen der Definition Schubspiegelung genügen.
Satz SCH/1
- Es sei 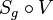eine Schubspieglung. Dann gilt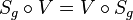
- Es sei
Beweis
- Es sei
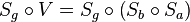
- Es sei
