Serie 03 zum 08.11.19
|
Aufgabe 03.01Bilden Sie die Umkehrung und Kontraposition und geben Sie den Wahreheitswert von Umkehrung und Kontraposition an: Aufgabe 03.02Drei Punkte heißen kollinear, wenn es eine Gerade gibt, auf der alle drei Punkte liegen. Geraden sind eindimensionale geometrische Objekte. Wir gehen eine Dimension höher und betrachten Ebenen. Das Pendant zu kollinear heißt komplanar. Defineren Sie den Begriff komplanar. Wie viele Punkte braucht man wenigstens, um sinnvoll davon sprechen zu können, dass eine Menge von Punkten komplanar ist? Aufgabe 03.03In der ebenen Inzidenzgeometrie wird durch das Axiom I.3 gefordert, dass wenigstens drei nicht kollineare Punkte existieren. Wie lautet das entsprechende Axiom für die räumliche Inzidenzgeometrie bzgl. der Komplanarität? Aufgabe 03.04Es seien A, B, C drei Punkte. Beweisen Sie: Aufgabe 03.05Beweisen Sie: Wenn zwei verschiedene Ebenen einen Punkt gemeinsam haben, dann haben sie eine Gerade gemeinsam. Aufgabe 03.06Wir setzen jetzt die Schulgeometrie voraus. Aufgabe 03.07Es gelte der Satz des Pythagoras. Aufgabe 03.08Wir setzen die Schulgeometrie voraus.
Es seien Aufgabe 03.09Nach Aufgabe 03.08 dürfte Ihnen das folgende leicht fallen. Aufgabe 03.10Definieren Sie den Begriff Nebenwinkel ohne dabei die Größe von Winkeln zu verwenden. |
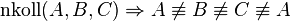 .
.
 ein Durchmesser des Kreises
ein Durchmesser des Kreises  .
.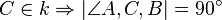 .
.
 eine rechtwinkliges Dreieck mit dem rechten Winkel bei
eine rechtwinkliges Dreieck mit dem rechten Winkel bei  . Die Kathete
. Die Kathete  bezeichnen wir mit
bezeichnen wir mit  und die andere Kathete mit
und die andere Kathete mit 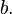
 sei der Fußpunkt der Höhe dieses Dreiecks auf die Hypotenuse
sei der Fußpunkt der Höhe dieses Dreiecks auf die Hypotenuse  . Der Hypotenusenabschnitt
. Der Hypotenusenabschnitt 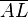 sei mit
sei mit 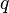 bezeichnet, der andere Hypotenusenabschnitt mit
bezeichnet, der andere Hypotenusenabschnitt mit  .
.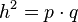 .
.
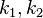 und
und 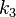 zwei Kreise mit den Mittelpunkten
zwei Kreise mit den Mittelpunkten 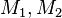 und
und 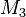 . Beweisen Sie: Wenn
. Beweisen Sie: Wenn 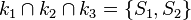 dann
dann 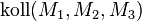 .
.
