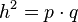|
Weil fast alle Hörer der Vorlesung diese wenigstens zum zweiten mal hören, wollte ich die Übungsaufgaben variieren und dem Kenntnistand anpassen. Aufgaben ausdenken ist ein kreativer Prozess und dauert seine Zeit. Ich bitte die Verspätung zu entschuldigen und habe als Wiedergutmachung die Aufgaben extra noch mal in TeX konvertiert und hier als PDF <document>Serie_2_12_13.pdf</document> abgelegt. Über eine Rückkopplung , wie Sie den Schwierigkeitsgrad der Aufgaben einschätzen, würde ich mich freuen. Viel Spaß beim Lösen der Aufgaben.--*m.g.* 18:15, 4. Nov. 2012 (CET)
Aufgaben zu Sätzen und Beweisen Teil 1
Aufgabe 2.1
Der Begriff Parallelogramm sei als Viereck mit zwei Paaren paralleler Seiten definiert. Wir betrachten die folgende Implikation (I):
(I) Wenn sich in einem Viereck die Diagonalen halbieren, dann ist das Viereck ein Parallelogramm.
(a) Nennen Sie die Voraussetzung und die Behauptung der Implikation (I).
(b) Bilden Sie die Umkehrung der Implikation (I).
(c) Bilden Sie die Kontraposition der Implikation (I).
(d) Beweisen Sie (I) mit den aus der Schule bekannten Sätzen.
(e) Beweisen Sie die Umkehrung der Implikation (I) mit den aus der Schule bekannten Sätzen.
(f) Definieren Sie den Begriff "Parallelogramm" neu.
Lösung Aufgabe 2.1 WS_12_13
Aufgabe 2.2
Der Satz des Pythagoras lautet:
Im rechtwinkligen Dreieck ist die Summer der Quadrate der Kathetenlängen gleich dem Quadrat der Länge der Hypotenuse.
(a) Formulieren Sie den Satz des Pythagoras in Wenn-Dann.
(b) Formulieren Sie die Umkehrung des Satzes von Pythagoras.
(c) Formulieren Sie die Kontraposition des Satzes von Pythagoras.
(d) Auch die Umkehrung des Satzes von Pythagoras ist wahr. Formulieren Sie ein Kriterium dafür, dass ein Dreieck rechtwinklig ist.
(e) Definieren Sie den Begriff des rechtwinkligen Dreiecks mittels des Kriteriums aus Teilaufgabe (d).
Lösung Aufgabe 2.2 WS_12_13
Aufgabe 2.3
Es gibt wahre Implikationen, deren Umkehrung nicht wahr ist. Formulieren Sie eine solche.
Beispiel:
Es seien 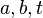 natürliche Zahlen. natürliche Zahlen.
Es gilt:
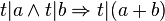
Es gilt nicht:
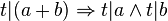
Lösung Aufgabe 2.3 WS_12_13
Aufgabe 2.4
Frau Schultze-Kröttendörfer hat mit ihrer 9a den Satz des Pythagoras behandelt. In der folgenden Stunde möchte sie überprüfen, ob die Schüler der 9a die Aussage des Satzes wirklich verstanden haben. Hierzu lässt sie die Schüler u.a. die folgende Aufgabe bearbeiten:
Rechtwinklig oder nicht?
Gegeben seien Dreiecke mit den folgenden Seitenlängen:
| Seitenlängen |
Dreieck 1 |
Dreieck 2 |
Dreieck 3 |
Dreieck 4 |
Dreieck 5
|
| a |
3 cm |
2 cm |
5 cm |
4,5 cm |
5 cm
|
| b |
4 cm |
3,61 cm |
2 cm |
4,5 cm |
12 cm
|
| c |
5 cm |
3 cm |
4 cm |
5 cm |
13 cm
|
Welche dieser Dreiecke sind mit Sicherheit nicht rechtwinklig? Begründe deine Entscheidungen.
(a) Kommentieren Sie diese Schüleraufgabe aus fachmathematischer Sicht unter Verwendung der Begriffe Implikation und Kontraposition.
(b) Wir unterstellen, dass die Schüler der 9a bis dato nur den Satz des Pythagoras kennen. Wegen zu vieler unbezahlter Vertretungsstunden ist Frau Schultze-Kröttendörfer überlastet. Infolge dieser Überlastung ist Frau Schultze-Kröttendörfer beim Entwurf der Frage zur obigen Aufgabe unkonzenriert und formuliert diese wie folgt:
Nenne alle Dreiecke der obigen Tabelle, die rechtwinklig sind. Begründe deine Entscheidungen.
Begründen Sie, warum die Schüler die Aufgabe jetzt nicht lösen könnten. Verwenden Sie in Ihrer Begründung den Begriff des Kriteriums.
Lösung Aufgabe 2.4 WS_12_13
Aufgabe 2.5
Der Satz des Pythagoras sei bewiesen. Es sei  ein Dreieck mit den schulüblichen Bezeichnungen: ein Dreieck mit den schulüblichen Bezeichnungen:
- Dem Punkt
 liegt die Seite liegt die Seite  gegenüber, dem Punkt gegenüber, dem Punkt  die Seite die Seite und dem Punkt und dem Punkt  die Seite c. die Seite c.
-
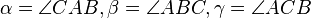 . .
Wir gehen davon aus, dass  rechtwinklig ist, wobei rechtwinklig ist, wobei  der rechte Winkel ist. der rechte Winkel ist. 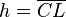 sei das Lot von sei das Lot von  auf auf  . Der Fußpunkt . Der Fußpunkt  des Lotes von des Lotes von  auf auf  teilt die Hypotenuse teilt die Hypotenuse  in die beiden Abschnitte in die beiden Abschnitte 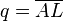 und und 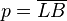 . .
Beweisen Sie den Höhensatz von Euklid:
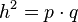
Lösung Aufgabe 2.5 WS_12_13
| 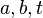 natürliche Zahlen.
natürliche Zahlen.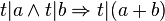
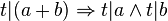
 ein Dreieck mit den schulüblichen Bezeichnungen:
ein Dreieck mit den schulüblichen Bezeichnungen: liegt die Seite
liegt die Seite  gegenüber, dem Punkt
gegenüber, dem Punkt  die Seite
die Seite und dem Punkt
und dem Punkt  die Seite c.
die Seite c.
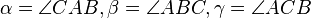 .
.
 der rechte Winkel ist.
der rechte Winkel ist. 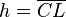 sei das Lot von
sei das Lot von  . Der Fußpunkt
. Der Fußpunkt  des Lotes von
des Lotes von 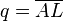 und
und 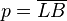 .
.