Umkehrung von Implikationen SoSe 2018: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> {|width=90%| style="backgro…“) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 2: | Zeile 2: | ||
{|width=90%| style="background-color:#FFFF99; padding:1em" | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| valign="top" | | | valign="top" | | ||
| + | =Allgemein= | ||
| + | Wir betrachten die Implikation <math>a \Rightarrow b</math>.<br /> | ||
| + | Die Implikation <math>b \Rightarrow a</math> ist die Umkehrung der Implikation <math>a \Rightarrow b</math>.<br /> | ||
| + | Wir vertauschen also die Rolle von Voraussetzung und Behauptung der Ausgangsimplikation.<br /> | ||
| + | Beide Implikationen, Ausgangsimplikation und zugehörige Umkehrung, müssen nicht zwangsläufig denselben Wahrheitsgehalt haben. | ||
| + | =Beispiele= | ||
| + | ==Beispiel 1== | ||
| + | ===Implikation=== | ||
| + | Wenn eine Zahl <math>9</math> ein Teiler von <math>a</math> ist, dann ist <math>3</math> auch ein Teiler von <math>a</math>.<br /> | ||
| + | Voraussetzung: <math>9 \mid a</math><br /> | ||
| + | Behauptung: <math>3 \mid a</math><br /> | ||
| + | Die Implikation ist wahr, wie der folgende Beweis zeigt:<br /> | ||
| + | Wir übersetzten die Voraussetzung: <math>9 \mid a</math><br /> bedeutet: <math>\exists n \in \mathbb{Z}: n \cdot 9 = a</math>.<br /> | ||
| + | Wir übersetzen die Behauptung: <math>3 \mis a</math> bedeutet: <math>\exists m \in \mathbb{Z}: 3 \cdot m= a</math>.<br /> | ||
| + | |||
| + | |||
| + | |||
| + | |||
Version vom 28. April 2018, 14:10 Uhr
AllgemeinWir betrachten die Implikation BeispieleBeispiel 1ImplikationWenn eine Zahl bedeutet:
|
 .
.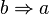 ist die Umkehrung der Implikation
ist die Umkehrung der Implikation 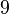 ein Teiler von
ein Teiler von  ist, dann ist
ist, dann ist  auch ein Teiler von
auch ein Teiler von 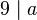
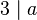
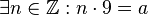 .
.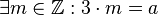 .
.
