Beispiele für Gruppen
endliche Gruppen
Die Gruppe der Deckabbildungen des Rechtecks
Die Gruppe der Deckabbildungen der Raute
unendliche Gruppen
Gebrochene Zahlen: ![[\mathbb{Q}^+, \cdot ]](/images/math/2/9/8/298e82ce4345a135cfc73e8ba6154d2b.png)
Ganze Zahlen: ![[\mathbb{Z}, +]](/images/math/8/2/8/828d3197747f0dc881f51c684f1a4c7d.png)
Gegenbeispiele für Gruppen
Gruppendefinitionen
Die "übliche" Gruppendefinition (lange Version)
Definition 1a: (Gruppe Langfassung)
Es sei  eine nichtleere Menge auf der eine Verknüpfung eine nichtleere Menge auf der eine Verknüpfung 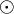 . .
Wenn die folgenden Axiome erfüllt sind, heißt die Struktur ![\mathbb{G}:=[G, \odot ]](/images/math/b/6/2/b62276da8758fad83c54ead688c9ecca.png) Gruppe: Gruppe:
-
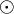 ist auf ist auf  abgeschlossen: abgeschlossen: 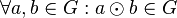
-
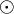 ist assoziativ auf ist assoziativ auf  : : 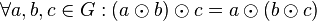
- Bezüglich
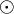 existiert in existiert in  ein ("universelles") Einslement ein ("universelles") Einslement  : : 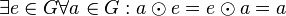 . .
- Bezüglich
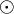 existiert zu jedem existiert zu jedem 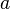 aus aus  ein ("persönliches") inverses Element ein ("persönliches") inverses Element 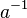 : :  . .
Die "übliche" Gruppendefinition (kurze Version)
Definition 1b: (Gruppe, Kurzfassung)
Es sei  eine nichtleere Menge auf der eine Verknüpfung eine nichtleere Menge auf der eine Verknüpfung 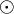 . .
Wenn die folgenden Axiome erfüllt sind, heißt die Struktur ![\mathbb{G}:=[G, \odot ]](/images/math/b/6/2/b62276da8758fad83c54ead688c9ecca.png) Gruppe: Gruppe:
-
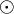 ist auf ist auf  abgeschlossen: abgeschlossen: 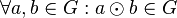
-
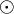 ist assoziativ auf ist assoziativ auf  : : 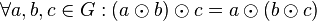
- Bezüglich
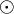 existiert in existiert in  ein ("universelles") Einslement ein ("universelles") Einslement  : : 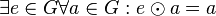 . .
- Bezüglich
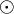 existiert zu jedem existiert zu jedem 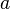 aus aus  ein ("persönliches") inverses Element ein ("persönliches") inverses Element 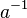 : : 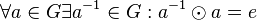 . .
Ordnung einer Gruppe
Definition 2: (Gruppenordnung)
- Unter der Ordnung einer Gruppe versteht man die Anzahl ihrer Elemente.
Kurzschreibweise: Wenn  die Ordnung der Gruppe die Ordnung der Gruppe  ist: ist: 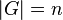
Ordnung einer Gruppenelements
Definition 3: (Ordung eines Gruppenelements)
Es sei ![[G,\odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) eine Gruppe mit dem Einselement eine Gruppe mit dem Einselement  und und  . Die kleinste natürliche Zahl . Die kleinste natürliche Zahl  mit mit  , für die gilt , für die gilt 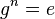 heißt Ordnung von heißt Ordnung von  . .
Kurzschreibweise: 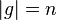
Halbgruppe
Definition 4: (Halbgruppe)
- Eine Menge
 auf der eine Verknüpfung auf der eine Verknüpfung  definiert ist, heißt Halbgruppe, wenn definiert ist, heißt Halbgruppe, wenn  abgeschlossen auf abgeschlossen auf 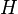 und assoziativ ist. und assoziativ ist.
Bemerkung: Tutor Alex wies darauf hin, dass die Menge 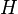 auch die leere Menge sein darf. Er hat recht. Ich habe das geändert.--*m.g.* (Diskussion) 16:43, 14. Mai 2017 (CEST)
(Bitte dazu in die Diskussion schauen! (Update)) auch die leere Menge sein darf. Er hat recht. Ich habe das geändert.--*m.g.* (Diskussion) 16:43, 14. Mai 2017 (CEST)
(Bitte dazu in die Diskussion schauen! (Update))
Monoid
Definition 5: (Monoid)
- Eine Halbgruppe mit Einselement heißt Monoid.
Das Linkseinslement ist auch Rechtseinselement
Die lange Version der Gruppendefinition fordert, dass wenn das Einselement  sowohl rechtsseitig als auch linksseitig multipliziert mit einem beliebigen Gruppenelement sowohl rechtsseitig als auch linksseitig multipliziert mit einem beliebigen Gruppenelement 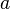 multipliziert eben dieses Element multipliziert eben dieses Element 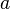 das Ergebnis dieser Multiplikation ist. Die kurze Version der Gruppendefinition fordert nur die Existenz eines linksseitigen Einslementes. In der Tat ist die Korrektheit der Gruppendefinition gewährleistet, wenn die Existenz des Einselementes nur linksseitig (oder rechtsseitig) gefordert wird.
Gleiches gilt für die Forderung nach der Existenz linksseitiger bzw. rechtsseitiger inverser Elemente. das Ergebnis dieser Multiplikation ist. Die kurze Version der Gruppendefinition fordert nur die Existenz eines linksseitigen Einslementes. In der Tat ist die Korrektheit der Gruppendefinition gewährleistet, wenn die Existenz des Einselementes nur linksseitig (oder rechtsseitig) gefordert wird.
Gleiches gilt für die Forderung nach der Existenz linksseitiger bzw. rechtsseitiger inverser Elemente.
Es gilt der Satz:
Satz 1
- Wenn in einer Halbgruppe ein linksseitiges Einselement und zu jedem Element der Halbgruppe ein linksseitiges inverses Element existiert, so sind dieses Linkseinselement und diese Linksinversen gleichzeitig Rechtseinselement und Rechtsinverse.
Beweis von Satz 1
Übungsaufgabe, Hinweise
- Beginnen Sie mit Linksinvers=Rechtsinvers
- Multiplizieren Sie zunächst das Linksinverse
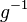 eines beliebigen Elementes eines beliebigen Elementes  von rechts mit von rechts mit  : :
- Ersetzen Sie
 durch durch 
- Ersetzen Sie
 durch das Produkt des Linksinversen vom Linksinversen von durch das Produkt des Linksinversen vom Linksinversen von  mit dem Linksinversen von mit dem Linksinversen von  : : 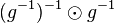 . .
- Der Rest ist geschicktes Klammern und Ausnutzung der Assoziativität...
Beweis:
Es sei 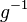 das Linksinverse von das Linksinverse von  . .
Wir muliplizieren 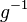 von rechts mit von rechts mit  : :
(I) 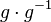
(II) 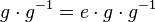
Wissen: Auch 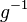 hat ein Linksinverses: hat ein Linksinverses: 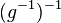
Ersetzen  durch durch 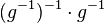
(III) 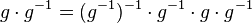
(IV) geschicktes Klammern: 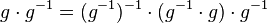
(V) Klammer berechnen: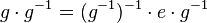
(VI) Mit  multiplizieren ist geschenkt ... multiplizieren ist geschenkt ... 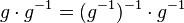
(VII) 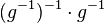 bedeutet, das Linksinverse vom Linksinversen von bedeutet, das Linksinverse vom Linksinversen von  mieinander multiplizieren. mieinander multiplizieren.
(VII) also 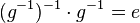
(IX) und damit 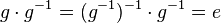
(X) oder einfach: 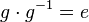 und damit: Das Linksinverse und damit: Das Linksinverse 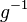 von von  ist auch sein Rechtsinverses ist auch sein Rechtsinverses
| 
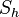
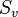
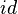
![[\mathbb{Q}^+, \cdot ]](/images/math/2/9/8/298e82ce4345a135cfc73e8ba6154d2b.png)
![[\mathbb{Z}, +]](/images/math/8/2/8/828d3197747f0dc881f51c684f1a4c7d.png)
 eine nichtleere Menge auf der eine Verknüpfung
eine nichtleere Menge auf der eine Verknüpfung 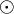 .
. ![\mathbb{G}:=[G, \odot ]](/images/math/b/6/2/b62276da8758fad83c54ead688c9ecca.png) Gruppe:
Gruppe: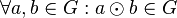
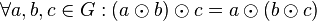
 :
: 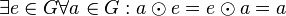 .
.
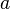 aus
aus 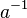 :
:  .
.
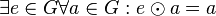 .
.
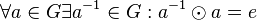 .
.
 die Ordnung der Gruppe
die Ordnung der Gruppe 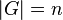
![[G,\odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) eine Gruppe mit dem Einselement
eine Gruppe mit dem Einselement 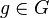 . Die kleinste natürliche Zahl
. Die kleinste natürliche Zahl 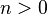 , für die gilt
, für die gilt 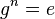 heißt Ordnung von
heißt Ordnung von  .
.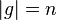
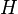 auf der eine Verknüpfung
auf der eine Verknüpfung 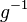 eines beliebigen Elementes
eines beliebigen Elementes 

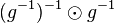 .
.
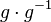
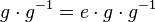
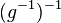
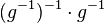
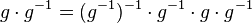
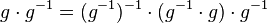
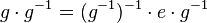
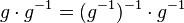
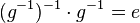
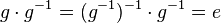
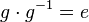 und damit: Das Linksinverse
und damit: Das Linksinverse 
