Was kann, was soll Abbildungsgeometrie in der Schule (2010)
Inhaltsverzeichnis |
Das Anliegen der Vorlesung
Bewegungen sind seit längerer Zeit integraler Stoff des Geometrieunterrichts der Schule. Bereits in der Primarstufe beschäftigen sich die Schüler mit achsensymmetrischen Figuren und in diesem Zusammenhang mit Geradenspiegelungen.
In letzter Zeit zeigen die Lehrbücher insbesondere der SI eine vergleichsweise geringere Gewichtung der Kongruenzabbildungen als etwa noch vor 5 Jahren. Eine Rückkehr zur eher statischen Kongruenzgeometrie auf der Grundlage der Dreieckskongruenz scheint sich anzubahnen.
Die Vorlesung soll aufzeigen wodurch dieser Paradigmenwechsel zustande kam. In diesem Zusammenhang wird aufgezeigt welche Probleme und welche Potenzen eine Kongruenzgeometrie auf abbildungsgeometrischer Grundlage für den Unterricht der Primar- und insbesondere der Sekundarstufe in sich birgt.
Noch einmal: die zwei Aspekte der Kongruenzgeometrie
| auf der Grundlage der Dreieckskongruenz | auf der Grundlage des Bewegungsbegriffs |
|---|---|
| Ausgangspunkt: Dreieckskongruenzsätze | Ausgangspunkt: Bewegungen als abstandserhaltende Abbildung |
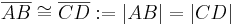
|
Es seien 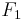 und und 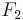 zwei Figuren. zwei Figuren. 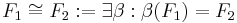
|
--Tetraeder 22:36, 15. Dez. 2010 (UTC)
Wege zur Definition des Begriffs der Kongruenzabbildung
- Allgemeiner Bewegungsbegriff → axiomatische Absicherung der Existenz von Bewegungen (Bewegungsaxiom) → Kongruenzabbildung als Synonym → spezielle Kongruenzabbildungen (Spiegelung, Drehung, Verschiebung).
- Geradenspiegelung → axiomatische Begründung von Geradenspiegelungen → Nacheinanderausführung von Geradenspiegelungen → Bewegung bzw. Kongruenzabbildung als Nacheinanderausführung zweier bzw. dreier Geradenspiegelungen.
- axiomatische Begründung der Dreieckskongruenz (SWS) → Definition der Bewegung als abstandserhaltende Abbildung der Ebene auf sich → Synonym Kongruenzabbildung → definition und Untersuchung spezieller Kongruenzabbildungen.
- axiomatische Begründung der Dreieckskongruenz (SWS) → Untersuchung von Geradenspiegelungen, Verschiebungen, Drehungen → Bewegung bzw. Kongruenzabbildung als Nacheinanderausführung von Spiegelungen, Verschiebungen und Drehungen.
Abbildungsgeometrische Beweise
Lange vorherrschende Meinung in der Mathematikdidaktik
Abbildungsgeometrische Beweise sind einfach, elegant, anschaulich und gut zu verstehen.
WIRKLICH????????
Beispiele
Beispiel 1
Satz
- Die Nacheinanderausführung zweier Drehungen
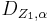 und
und 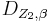 mit
mit 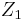 und
und 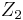 sind verschieden voneinander ist entweder eine Drehung oder eine Verschiebung.
sind verschieden voneinander ist entweder eine Drehung oder eine Verschiebung.
- Die Nacheinanderausführung zweier Drehungen
Beweis
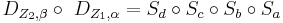
Ist das was für Schüler der SI?
Beispiel 2
Der Basiswinkelsatz
- Wenn ein Dreieck gleichschenklig ist, dann sind seine Basiswinkel kongruent zueinander.
Wie man leicht sieht, wird das Dreieck  bei einer Spiegelung an
bei einer Spiegelung an 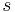 auf sich selbst abgebildet. Also wird auch ein Basiswinkel auf den jeweils anderen Basiswinkel abgebildet. also sind die beiden Basiswinkel gleich groß.
auf sich selbst abgebildet. Also wird auch ein Basiswinkel auf den jeweils anderen Basiswinkel abgebildet. also sind die beiden Basiswinkel gleich groß.
IST DAS EIN BEWEIS ????????
Beispiel 3
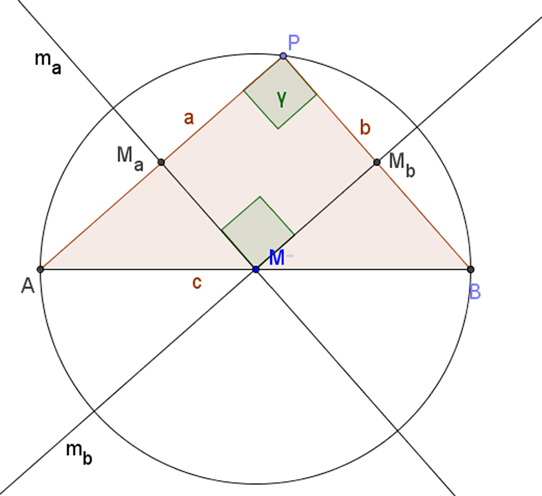
Satz des Thales
- Jeder Peripheriewinkel über einem Durchmesser ist ein Rechter.
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 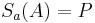
|
a ist Mittelsenkrechte von AP |
| (II) | 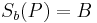
|
b ist Mittelsenktrechte von PB |
| (III) | 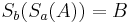
|
(I),(II) HIntereinanderführung zweier Spiegelungen ist eine eindeutige Bewegung |
| (IV) | (III) ist eine Drehung um 180° | koll(A,M,B);da M nach dem Mittelsenkrechtenkriterium auf AB liegen muss |
| (V) | 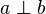
|
(IV) und einem Satz über den Drehungswinkel |
| (VI) | y = 90° | (I), (II), (V) Innenwinkelsumme im Viereck |
--Tja??? 16:39, 14. Dez. 2010 (UTC)
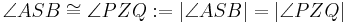
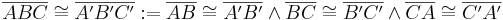
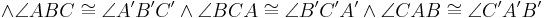
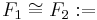 alle Strecken und alle Winkel von
alle Strecken und alle Winkel von 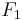 konkruent zu
konkruent zu 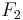 sind (???)
sind (???)