Zu den Lösungen Serie 04 WiSe 2011/12
Inhaltsverzeichnis |
Aufgabe 4.1
Es seien  drei nichtkollineare Punkte und
drei nichtkollineare Punkte und 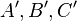 ihre Bilder bei der Bewegung
ihre Bilder bei der Bewegung  . Man beweise: Für jeden Punkt
. Man beweise: Für jeden Punkt  ist jetzt sein Bild
ist jetzt sein Bild 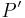 bei
bei  eindeutig bestimmt.
eindeutig bestimmt.
Voraussetzung: nkoll(A,B,C) sowie A', B' und C' und P
Behauptung: 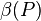 = P' ist eindeutig bestimmt für jede Abbildung.
= P' ist eindeutig bestimmt für jede Abbildung.
Es sind nun verschiedene Fälle zu betrachten. Der einfachste Fall ist, dass alle Punkte Fixpunkte sind, dann haben wir - nach dem vorherigen Satz gezeigt - die Identität. In diesem Fall spielt es keine Rolle, ob 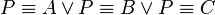 oder ob P verschieden von A, B oder C ist. In diesen Fällen sind wir fertig.
oder ob P verschieden von A, B oder C ist. In diesen Fällen sind wir fertig.
Nun Fall II: Bewegung ist nicht die Identität (hier spielt es übrigens schon eine Rolle, ob P verschieden ist von A, B oder C oder nicht. Da die Voraussetzung nicht erfüllt werden kann, wenn P nicht verschieden ist von den drei nichtkollinearen Punkten (kann durch eine Mittelsenkrechte ganz leicht gezeigt werden) nehmen wir an, dass dem nicht der Fall ist, also P ungleich A, B, C.
Bei der Bewegung bleiben die Abstände erhalten. Fehler beim Parsen(Syntaxfehler): \\left| AB \right|
=. Weiter bleibt nun
.
Nun kann P (und somit auch später P') in zwei Halbebenen bzgl. AB liegen oder auf AB selbst. Wenn P aber auf AB liegt, sind wir fertig, denn dann ergibt sich nur eine Möglichkeit wegen der Zwischenrelation.
Da nun aber zusätzlich gelten muss, dass 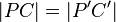 ist nun folgendes unmittelbar einleuchtend und ersichtlich:
ist nun folgendes unmittelbar einleuchtend und ersichtlich:
Wenn P und C bzgl. AB in verschiedenen Halbebenen liegen, liegen auch P' und C' in verschiedenen Halbebenen bzgl. AB. Wenn P und C bzgl. AB in ein und derselben Halbebene liegen, liegen auch P' und C' in ein und derselben Halbebene bzgl. AB. Demnach ist P' eindeutig.
Ich werde das ganze evtl. nochmal schöner schreiben, da es vielleicht verwirrend ist. Wenn mein Geogebra wieder funktioniert, schicke ich eine Applikation nach. --Flo60 20:21, 15. Nov. 2011 (CET)
Des ist ja Humbug - des geht ja viel einfacher :-)
Voraussetzung: 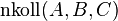 , die Bilder der Punkte bzgl.
, die Bilder der Punkte bzgl.  seine A', B' und C'
seine A', B' und C'
Behauptung: 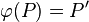 ist eindeutig bestimmt.
ist eindeutig bestimmt.
Beweis durch Widerspruch
Annahme: 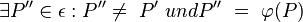
| Nummer | Beweisschritt | Begründung |
|---|---|---|
| 1 | AP| = |A'P'| = |A'P| | Definition Bewegung, Voraussetzung und Annahme, dass 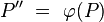
|
| 2 | BP| = |B'P'| = |B'P| | Definition Bewegung, Voraussetzung und Annahme, dass 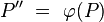
|
| 3 | CP| = |C'P'| = |C'P| | Definition Bewegung, Voraussetzung und Annahme, dass 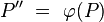
|
| 4 | Weil sowohl A' als auch B' und C' zu den Endpunkten der Strecke 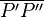 jeweils ein und denselben Abstand haben liegen sie allesamt auf der Mittelsenkrechten dieser Strecke. jeweils ein und denselben Abstand haben liegen sie allesamt auf der Mittelsenkrechten dieser Strecke. |
(1), (2), (3), Mittelsenkrechtenkriterium |
| 5 | Es gilt: 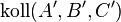 |
(4) |
| 6 | 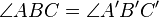 und und 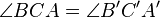 und und 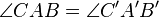 |
Satz der Winkeltreue bei Bewegungen |
| 7 | A, B und C sind ebenfalls kollinear | (5), (6) |
| 8 | Widerspruch zur Voraussetzung, dass 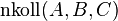 - Annahme ist zu verwerfen - Annahme ist zu verwerfen |
(7) |
--Flo60 14:39, 11. Dez. 2011 (CET)
Aufgabe 4.2
Es seien  und
und  zwei Geraden, die sich in genau dem Punkt
zwei Geraden, die sich in genau dem Punkt  schneiden. Man beweise:
Die Nacheinanderausführung
schneiden. Man beweise:
Die Nacheinanderausführung 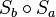 ist eine Drehung um Z, wobei der Drehwinkel dieser Drehung doppelt so groß ist wie der Winkel zwischen den beiden Geraden
ist eine Drehung um Z, wobei der Drehwinkel dieser Drehung doppelt so groß ist wie der Winkel zwischen den beiden Geraden  und
und  .
.
VSS: Die Geraden  und
und  schneiden sich in dem Punkt
schneiden sich in dem Punkt  .
Behauptung: 1.
.
Behauptung: 1. 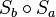 ist eine Drehung um
ist eine Drehung um  . --> Trivial nach Satz der VL vom 8.11.: Die NAF zweier Spiegelungen mit sich schneidender Spiegelachsen ist eine Drehung.
2. Drehwinkel alpha ist doppelt so groß, wie der Winkel zwischen den Geraden
. --> Trivial nach Satz der VL vom 8.11.: Die NAF zweier Spiegelungen mit sich schneidender Spiegelachsen ist eine Drehung.
2. Drehwinkel alpha ist doppelt so groß, wie der Winkel zwischen den Geraden  und
und  .
.
zu 2.:
1. a ist Mittelsenkrechte von 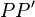 --> |
--> |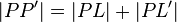 , weil L (Lotfußpunkt) Element a --> L ist Fixpunkt bei Spiegelung an a und es gilt das Mittelsenkrechtenkriterium
, weil L (Lotfußpunkt) Element a --> L ist Fixpunkt bei Spiegelung an a und es gilt das Mittelsenkrechtenkriterium
2.Z istz Fixpunkt 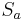 -->|
-->|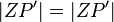 , weil L (Lotfußpunkt) Element a --> L ist Fixpunkt bei Spiegelung an a und es gilt das Mittelsenkrechtenkriterium
, weil L (Lotfußpunkt) Element a --> L ist Fixpunkt bei Spiegelung an a und es gilt das Mittelsenkrechtenkriterium
3. |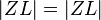 , weil L Element a und deshalb Fixpunkt (Definition 3.3 Fixpunktgerade)
, weil L Element a und deshalb Fixpunkt (Definition 3.3 Fixpunktgerade)
4. Die Dreiecke LPZ und LP'Z sind kongruent zueinander (SSS)
5. b ist Mittelsenkrechte vin P'P mit Lotfußpunkt J --> (gleiche Begründungen wie bei 1.)
6. Die Dreiecke P'ZJ und JZP sind kongruent zueinander (habe die Schritte von oben übersprungen, weil sie analog sind.)
7. Der Winkel (LZJ') ist genau so groß wie der der Dreiecke (LZP') addiert mit dem Winkel (P'ZJ).
8. Da bereits bewiesen wurde, dass die Dreiecke (LZP') und (P'ZJ je Kongruent zu den "Nachbardreiecken" (LZP) und (JZP) sind, ergibt sich daraus, dass der Drehwinkel alpa genau doppelt so groß sein muss, wie der Winkel zwischen den beiden Geraden a b. (Puh fertig aufgeschrieben!! Alles klar? :-D) Pipi Langsocke 17:43, 16. Nov. 2011 (CET)
Und noch kurz ikonisch nachgeschickt:
--Flo60 20:45, 20. Apr. 2012 (CEST)
Aufgabe 4.3
Sie haben mit Ihren Schülern den begriff der Drehung erarbeitet. Jetzt steht eine Erstfestigung an. Entwickeln Sie Fragestellungen, die sich auf die folgende Geogebra-Applikation beziehen und der Festigung des Begriffs der Drehung dienen. Beispiele:
- Der Punkt
 wird bei einer Drehung um
wird bei einer Drehung um  auf den Punkt
auf den Punkt  abgebildet. Wie groß ist der Drehwinkel dabei?
abgebildet. Wie groß ist der Drehwinkel dabei?
- Ist es möglich, dass bei einer Drehung um
 der Punkt
der Punkt 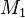 auf den Punkt
auf den Punkt  abgebildet wird?
abgebildet wird?
Aufgabe 4.4
Sowohl die Punkte 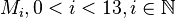 als auch die Punkte
als auch die Punkte 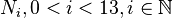 sind zueinander Bilder bei Drehungen um das Zentrum
sind zueinander Bilder bei Drehungen um das Zentrum 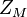 bzw.
bzw. 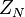 . Berechnen Sie die Koordinaten dieser Drehzentren.
. Berechnen Sie die Koordinaten dieser Drehzentren.
Wir benötigen hierzu den Vektor. Da wir schlussendlich vom Drehzentrum Z ausgehen, ist es sehr günstig, dass dieser Punkt den Ursprung markiert, das erleichtert uns die Sache ein bischen, aber nicht der Rede wert.
Wie berechnen wir den Vektor?
Weil wir es ja mit einer Verschiebung zu tun haben, und das Drehzentrum von (o. B. d. A.) A in gleicher Positionierung zu M steht, wie A zu M1, können wir damit rechnen.
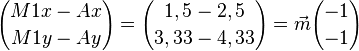 Diesen
Diesen 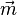 Vektor müssen wir nun an Z ansetzen und Punkt Z daran verschieben. Das Bild von m(Z) ist dann folgen M.
Vektor müssen wir nun an Z ansetzen und Punkt Z daran verschieben. Das Bild von m(Z) ist dann folgen M.
Warum weiß ich, dass ich die A - Koordinaten von den M1 - Koordinaten abziehen muss und nicht andersherum? Das ist unmittelbar ersichtlich, da ich einen negativen Richtungssinn sowohl auf der x-Achse, als auch auf der y-Achse.
Meine Ausdrucksweise hier ist irgendwie kompliziert. Wenn jemand ein paar gute Bezeichnungen für den ganzen Sums hier hat, der schreibe hier bitte vergnüglich ein paar (brauchbare) Aspekte an.
Zur Findung des dritten Drehzentrums geht man analog vor ODER berechnet direkt von M aus die Veränderung der X-Koordinaten, da MN immer parallel zur X-Achse scheint.
--Flo60 22:53, 22. Nov. 2011 (CET)

