Übung Aufgaben 4 (WS 14/15)
Inhaltsverzeichnis |
Aufgabe 4.1
a) Definieren Sie die Begriffe: "gleichseitiges Dreieck" und "gleichschenkliges Dreieck". Die Begriffe "Dreieck" und "Seite eines Dreiecks" seien bereits definiert.
b) Beweisen Sie durch Kontraposition: Jedes gleichseitige Dreieck ist auch ein gleichschenkliges Dreieck.
Lösung von Aufgabe 4.1_P (WS_14/15)
Aufgabe 4.2
Satz: Gegeben sei ein Dreieck  in einer Ebene E und eine Gerade g in dieser Ebene, die keine der drei Punkte A, B und C enthält.
Wenn g die Strecke
in einer Ebene E und eine Gerade g in dieser Ebene, die keine der drei Punkte A, B und C enthält.
Wenn g die Strecke  schneidet, so schneidet sie auch entweder die Strecke
schneidet, so schneidet sie auch entweder die Strecke  oder die Strecke
oder die Strecke  .
.
a) Wie lautet die Kontraposition dieser Implikation?
b) Wie lautet die Annahme, wenn Sie diese Implikation durch einen Widerspruch beweisen möchten?
Lösung von Aufgabe 4.2_P (WS_14/15)
Aufgabe 4.3
a) Geben Sie die Menge  aller konvexer Drachenvierecke an.
aller konvexer Drachenvierecke an.
b) Bilden Sie das kartesische Produkt der Menge  .
.
c) Wir definineren eine Relation  mit
mit 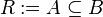 . Bestimmen Sie die Relation
. Bestimmen Sie die Relation  auf
auf  .
.
d) Untersuchen Sie die Relation  auf ihre Eigenschaften (reflexiv, symmetrisch, transitiv).
auf ihre Eigenschaften (reflexiv, symmetrisch, transitiv).
Lösung von Aufgabe 4.3_P (WS_14/15)
Aufgabe 4.4
Entscheiden Sie für die folgenden Relationen, ob es sich um reflexive, symmetrische sowie transitive Relationen handelt?
- Parallelität von Geraden der Ebene
- Kongruenz geometrischer Figuren
- Teilbarkeit in

- Kleinerrelation in

- Größer-Gleich-Relation in

- Ungleichheit in

Lösung von Aufgabe 4.4_P (WS_14/15)
Aufgabe 4.5
Untersuchen Sie folgende Relation S auf ihre Eigenschaften:
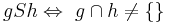
Lösung von Aufgabe 4.5_P (WS_14/15)
Aufgabe 4.6
Es seien eine Ebene E (aufgefasst als Punktmenge) und eine Gerade g in E gegeben. Wir betrachten folgende Relation  (
( ist ein willkürlich gewähltes Symbol, um die Relation nicht mit dem unauffälligen Buchstaben R bezeichnen zu müssen) in der Menge
ist ein willkürlich gewähltes Symbol, um die Relation nicht mit dem unauffälligen Buchstaben R bezeichnen zu müssen) in der Menge 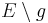 (also alle Punkte der Ebene E, die nicht der Geraden g angehören): Für beliebige
(also alle Punkte der Ebene E, die nicht der Geraden g angehören): Für beliebige 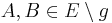 gilt:
gilt: 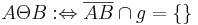 .
.
a) Beschreiben Sie die Relation  verbal und veranschaulichen Sie diese Relation.
verbal und veranschaulichen Sie diese Relation.
b) Begründen Sie anschaulich, dass  eine Äquivalenzrelation ist. Formulieren Sie dazu die Eigenschaften von Äquivalenzrelationen konkret auf die Relation
eine Äquivalenzrelation ist. Formulieren Sie dazu die Eigenschaften von Äquivalenzrelationen konkret auf die Relation  bezogen.
bezogen.
Hinweis: Sie können die Transitivität noch nicht exakt beweisen; in dieser Aufgabe geht es zunächst darum, die Relationseigenschaften als geometrische Eigenschaften zu interpretieren und zu verstehen.
Lösung von Aufgabe 4.6_P (WS_14/15)

