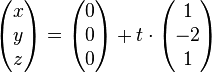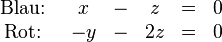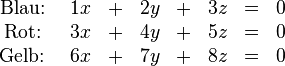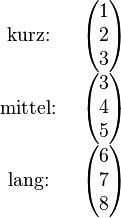Die Koeffizientenmatrix
So ist es, wenn man sich schnell in der Vorlesung ein Gleichungssystem einfallen lässt.
Zur Erinnerung: an der Tafel entstand spontan eine Koeffizientenmatrix vom folgenden Typ:
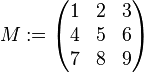 Wir wollten den Rang (die Anzahl der linear unabhängigen Zeilen) dieser Matrix bestimmen und waren zunächst davon überzeugt, dass diese spezielle Wahl darauf hinaus laufen müsste, dass alle die Zeilen der Matrix
Wir wollten den Rang (die Anzahl der linear unabhängigen Zeilen) dieser Matrix bestimmen und waren zunächst davon überzeugt, dass diese spezielle Wahl darauf hinaus laufen müsste, dass alle die Zeilen der Matrix  linear unabhängig sein würden und unsere Matrix damit den Rang linear unabhängig sein würden und unsere Matrix damit den Rang  haben würde.
Völlig erstaunt waren wir als wir konstatieren mussten, dass die dritte Zeile eine Linearkombination der ersten beiden Zeilen ist. Natürlich kann man den Algorithmus zur Generierung der Diagonalenform der Matrix anwenden, so wie wir es taten. Mehr Überzeugungskraft hat jedoch die Betrachtung des Schemas, wie die Matrix haben würde.
Völlig erstaunt waren wir als wir konstatieren mussten, dass die dritte Zeile eine Linearkombination der ersten beiden Zeilen ist. Natürlich kann man den Algorithmus zur Generierung der Diagonalenform der Matrix anwenden, so wie wir es taten. Mehr Überzeugungskraft hat jedoch die Betrachtung des Schemas, wie die Matrix  entsteht: entsteht:
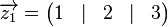
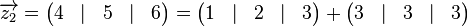
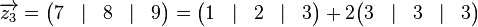
Den Zeilenvektor 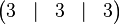 bezeichnen wir kurz mit bezeichnen wir kurz mit 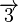 . .
Damit können wir  wie folgt schreiben: wie folgt schreiben: 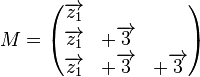 . .
Jetzt sieht man leicht, dass 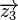 eine Linearkombination von eine Linearkombination von 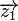 und und 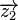 ist: ist:
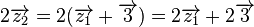
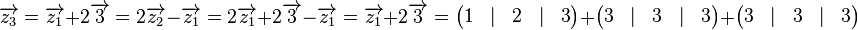 . .
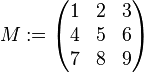 war die Matrix, die ich eigentlich an die Tafel bringen wollte. Stattdessen schrieb ich war die Matrix, die ich eigentlich an die Tafel bringen wollte. Stattdessen schrieb ich 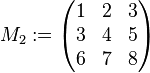 . Der Beweis für . Der Beweis für  funktioniert analog. Überzeugen Sie sich davon. Viel Spaß dabei --*m.g.* (Diskussion) 15:55, 24. Mai 2018 (CEST) funktioniert analog. Überzeugen Sie sich davon. Viel Spaß dabei --*m.g.* (Diskussion) 15:55, 24. Mai 2018 (CEST)
Die Matrix aus der Vorlesung
Die 3.Zeile ist eine Linearkombination der beiden anderen Zeilen
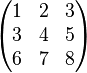
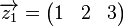
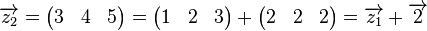
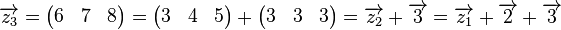
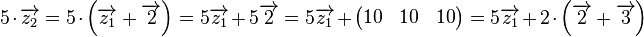
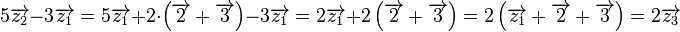
Also:
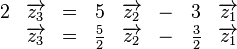
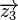 ist damit eine Linearkombination der Vektoren ist damit eine Linearkombination der Vektoren 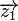 und und 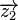 . .
Die beiden oberen Zeilen sind linear unabhängig
Bei der Untersuchung der linearen Unabhängigkeit von zwei Zeilen geht es nur darum, ob eine Zeile aus der anderen Zeile durch Multiplikation mit einer reellen Zahl hervorgeht:
Gesucht ist also 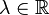 mit mit 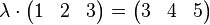
Eine solche Zahl 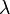 existiert nicht. Zeile 1 und Zeile 2 bilden zusammen eine Menge linear unabhängiger Zeilenvektoren. existiert nicht. Zeile 1 und Zeile 2 bilden zusammen eine Menge linear unabhängiger Zeilenvektoren.
Der Rang der kleinen Koeefizientenmatrix
Die Matrix 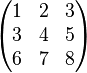 hat damit den Rang hat damit den Rang 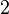 : :
Die Anzahl der linear unabhängigen Zeilenvektoren der Menge 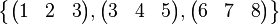 ist 2. ist 2.
Die mehr algorithmische Vorgehensweise aus der Vorlesung
Ausgangsmatrix
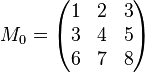
Schritt 1
Zeile 1 mit 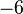 multiplizieren und dann zu Zeile 3 addieren. multiplizieren und dann zu Zeile 3 addieren.
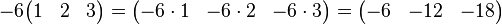
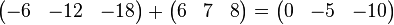
Wir erhalten die folgende Matrix:
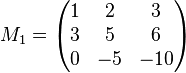
Schritt 2
Zeile 1 mit 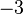 multiplizieren und zu Zeile 2 addieren: multiplizieren und zu Zeile 2 addieren:
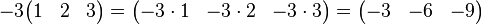
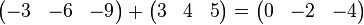
Wir erhalten die folgende Matrix:
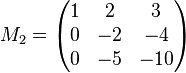
Schritt 3
Wir multiplizieren die zweite Zeile aus  mit mit 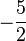 und addieren sie dann zu Zeile 3 in und addieren sie dann zu Zeile 3 in 
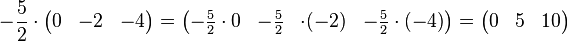
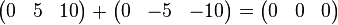
Wir erhalten die folgende Matrix:
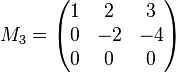
Der Rang unserer Ausgangsmatrix (wie der Matrix 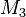 ) kann damit nicht mehr ) kann damit nicht mehr  sondern nur noch höchstens sondern nur noch höchstens 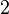 sein. sein.
Schritt 4
Wir addieren die zweite Zeile der Matrix 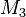 zur ersten Zeile der Matrix zur ersten Zeile der Matrix 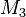 und erhalten: und erhalten:
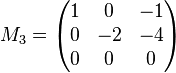
Wir vereinfachen:
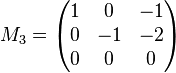
Weitere Vereinfachungen sind nicht mehr möglich, unsere Matrix hat den Rang 2.
Geometrische Interpretation der Matrix und des LGS
Lösungsgerade
Wir ergänzen zum sogenannten homogenen LGS:
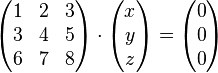
bzw.
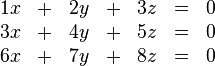
Da wir das homogene LGS betrachten, können wir auch unmittelbar die vereinfachten Matrizen verwenden:
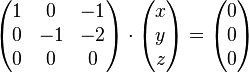
bzw.
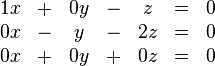
oder noch einfacher:
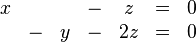
bzw.

Es ergibt sich damit die folgende Lösungsmenge  für unser homogenes LGS: für unser homogenes LGS:
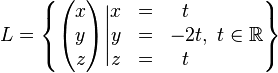
Wir erkennen einen proportionalen Zusammenhang jeweils zwischen den 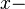 Werten, Werten, 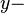 Werten und Werten und 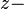 Werten. Werten.
Die Lösungsmenge  lässt sich also als die Menge der Koordinaten der Punkte einer Geraden lässt sich also als die Menge der Koordinaten der Punkte einer Geraden  interpretieren. Diese Gerade geht u.a. durch die Punkte interpretieren. Diese Gerade geht u.a. durch die Punkte 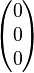 und und 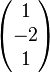 . Wir schreiben die Gleichung der Geraden . Wir schreiben die Gleichung der Geraden  in Parameterform: in Parameterform: 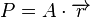 mit mit 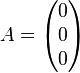 und und 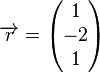 und damit und damit 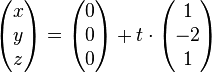
Grafische Darstellung der Lösungsgeraden in Geogebra
nur die Gerade
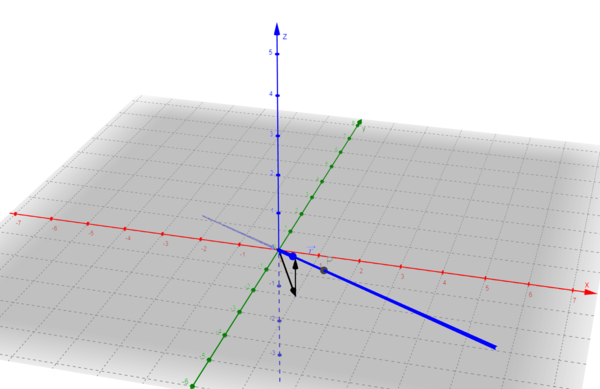
Lösungsgerade auf Geoegebra Tube
mit den Ebenen der vereinfachten Koeffizientenmatrix
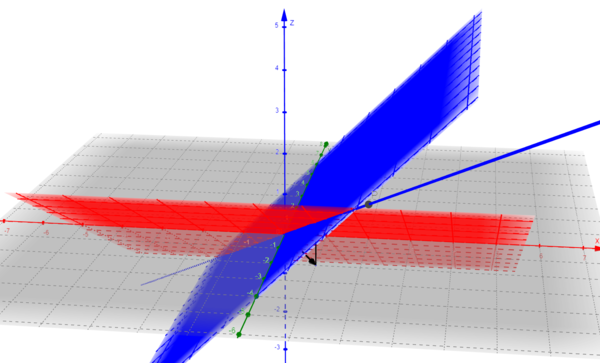
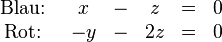
Lösungsgerade mit einfachen Ebenen auf Geoegebra Tube
mit den Ebenen der Ausgangsmatrix und den Normalenvektoren der Ausgangsebenen
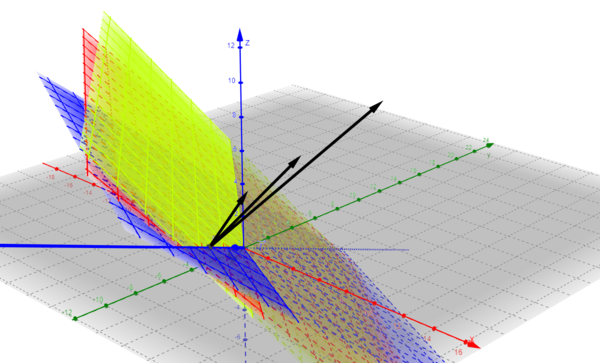
Ebenen
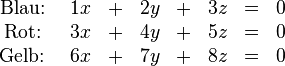
Normalenvektoren
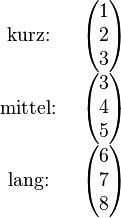
Die Datei auf Geogebra Tube
Wir sehen, dass die drei Normalenvektoren komplanar sind. Sie können Sich die Ebene in der Geogebradatei anzeigen lassen (Ebene f).
| 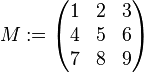 Wir wollten den Rang (die Anzahl der linear unabhängigen Zeilen) dieser Matrix bestimmen und waren zunächst davon überzeugt, dass diese spezielle Wahl darauf hinaus laufen müsste, dass alle die Zeilen der Matrix
Wir wollten den Rang (die Anzahl der linear unabhängigen Zeilen) dieser Matrix bestimmen und waren zunächst davon überzeugt, dass diese spezielle Wahl darauf hinaus laufen müsste, dass alle die Zeilen der Matrix  linear unabhängig sein würden und unsere Matrix damit den Rang
linear unabhängig sein würden und unsere Matrix damit den Rang  haben würde.
Völlig erstaunt waren wir als wir konstatieren mussten, dass die dritte Zeile eine Linearkombination der ersten beiden Zeilen ist. Natürlich kann man den Algorithmus zur Generierung der Diagonalenform der Matrix anwenden, so wie wir es taten. Mehr Überzeugungskraft hat jedoch die Betrachtung des Schemas, wie die Matrix
haben würde.
Völlig erstaunt waren wir als wir konstatieren mussten, dass die dritte Zeile eine Linearkombination der ersten beiden Zeilen ist. Natürlich kann man den Algorithmus zur Generierung der Diagonalenform der Matrix anwenden, so wie wir es taten. Mehr Überzeugungskraft hat jedoch die Betrachtung des Schemas, wie die Matrix 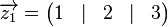
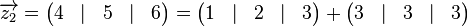
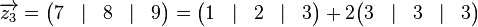
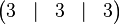 bezeichnen wir kurz mit
bezeichnen wir kurz mit 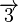 .
.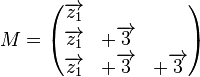 .
.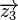 eine Linearkombination von
eine Linearkombination von 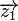 und
und 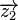 ist:
ist: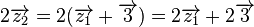
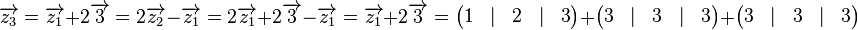 .
.
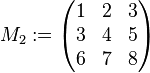 . Der Beweis für
. Der Beweis für  funktioniert analog. Überzeugen Sie sich davon. Viel Spaß dabei --
funktioniert analog. Überzeugen Sie sich davon. Viel Spaß dabei --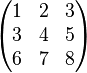
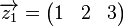
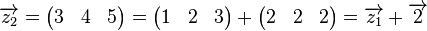
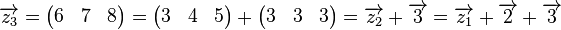
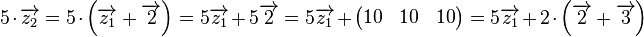
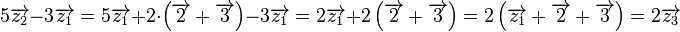
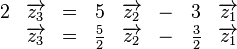
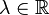 mit
mit 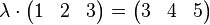
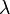 existiert nicht. Zeile 1 und Zeile 2 bilden zusammen eine Menge linear unabhängiger Zeilenvektoren.
existiert nicht. Zeile 1 und Zeile 2 bilden zusammen eine Menge linear unabhängiger Zeilenvektoren.
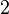 :
: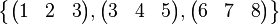 ist 2.
ist 2.
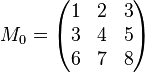
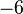 multiplizieren und dann zu Zeile 3 addieren.
multiplizieren und dann zu Zeile 3 addieren.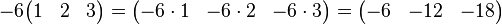
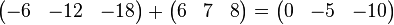
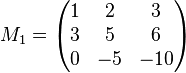
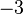 multiplizieren und zu Zeile 2 addieren:
multiplizieren und zu Zeile 2 addieren:
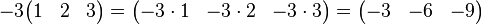
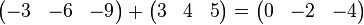
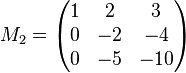
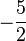 und addieren sie dann zu Zeile 3 in
und addieren sie dann zu Zeile 3 in 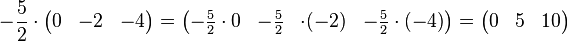
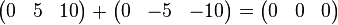
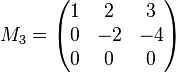
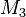 ) kann damit nicht mehr
) kann damit nicht mehr 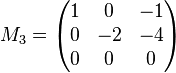
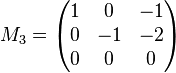
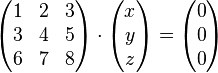
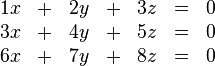
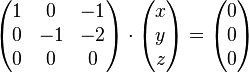
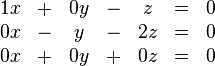
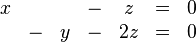

 für unser homogenes LGS:
für unser homogenes LGS:
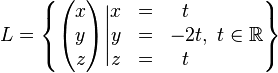
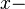 Werten,
Werten, 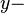 Werten und
Werten und 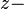 Werten.
Werten. interpretieren. Diese Gerade geht u.a. durch die Punkte
interpretieren. Diese Gerade geht u.a. durch die Punkte 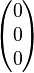 und
und 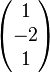 . Wir schreiben die Gleichung der Geraden
. Wir schreiben die Gleichung der Geraden 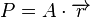 mit
mit 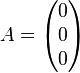 und
und 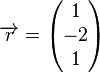 und damit
und damit