Lösung von Aufgabe 6.2
Das Axiom I.7 sagt aus:
Es gibt vier Punkte, die nicht komplanar sind.
Es sei  eine beliebige Ebene und
eine beliebige Ebene und  die vier Punkte entsprechend Axiom I.7. Klassifizieren Sie alle Fälle die bezüglich der Inzidenz der Punkte
die vier Punkte entsprechend Axiom I.7. Klassifizieren Sie alle Fälle die bezüglich der Inzidenz der Punkte  mit
mit  auftreten können.
auftreten können.
Lösung: --Schnirch 11:56, 16. Jun. 2010 (UTC)
Voraussetzung: Eine beliebige Ebene E und vier nicht komplanare Punkte A, B, C, D.
- alle vier Punkte können nicht in einer Ebene liegen (nach Voraussetzung)
- die Ebene E kann drei der vier Punkte enthalten (z. B. A, B und C)
- die Ebene E kann zwei der vier Punkte enthalten (z. B. A und B)
- die Ebene E kann einen der vier Punkte enthalten (z. B. A)
- die Ebene E kann keinen der vier Punkt enthalten.
vorangegangene Diskussion:
Voraussetzung: Die Punkte sind nicht kollinear.
Wenn mehr als zwei Punkte kollinear sind (zB. 
 Gerade g), dann sind diese Punkte und der verbleibende nichtkollineare Punkt (im Bsp.
Gerade g), dann sind diese Punkte und der verbleibende nichtkollineare Punkt (im Bsp. 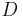 ) Elemente der Ebene
) Elemente der Ebene  .
.
Begründung:
Axiom I/4
Zu je drei nichtkollinearen Punkten gibt es genau eine Ebene, die diese drei Punkte enthält. (...)
Axiom I/5
Wenn zwei Punkte einer Geraden g in einer Ebene E liegen, so gehört g zu E.
Der Fall, dass alle vier Punkte kollinear sind (also 
 Gerade g) ist dann trivial, da durch Definition I/4 abgedeckt.
Gerade g) ist dann trivial, da durch Definition I/4 abgedeckt.
| Fall | Bsp/Ausprägung | Zusatz | nKomp |
DREI Punkte liegen in  (sind Elemente von...) (sind Elemente von...) |
 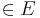 |
mögliche Tripel:  1(A,B,C) 1(A,B,C)  2(A,B,D) 2(A,B,D)  3(A,C,D) 3(A,C,D)  4 (B,C,D) 4 (B,C,D) |
 1(D) 1(D)  2(C) 2(C)  3(B) 3(B)  4 (A) 4 (A)
|
| VIER Punkte sind komplanar |  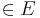 |
alle Punkte liegen "auf" / "in" Ebene  |
keine Punkt nKomp |
Mehr Fälle gibt es nach der Vorraussetzung nicht, oder?
--Heinzvaneugen
Du hast was falsch verstanden, Heinzvaneugen.
Die Voraussetzung ist, dass die Punkte nicht komplanar sind. Damit sind auf jeden Fall keine drei Punkte davon kollinear.
Der höchstmögliche Fall ist also, dass drei Punkte in der Ebene liegen.
Außerdem ist zu beachten, dass  eine beliebige Ebene ist. Die Punkte können z.B. alle miteinander weit entfernt von der Ebene liegen. Oder die Ebene geht "zwischendurch". Das wäre zweimal der gleiche Fall, nämlich dass kein Punkt in der Ebene liegt.
eine beliebige Ebene ist. Die Punkte können z.B. alle miteinander weit entfernt von der Ebene liegen. Oder die Ebene geht "zwischendurch". Das wäre zweimal der gleiche Fall, nämlich dass kein Punkt in der Ebene liegt.
Die beiden verbleibenden Fälle liegen jetzt wahrscheinlich auf der Hand...
--Sternchen 10:45, 5. Jun. 2010 (UTC)
Also wenn ich die Erklärung von Sternchen richtig verstanden habe, dann gibt es vier Fälle:
1) komp(A,B,C)
2) komp (A,B)
3) komp (A)
4) nkomp (A,B,C,D)
Stimmt das so, und ist die Schreibweise korrekt?
--Gänseblümchen 12:16, 6. Jun. 2010 (UTC)
- Ja, die vier Fälle hatte ich gemeint und nein, die Schreibweise ist nicht korrekt. Die richtige Schreibweise wäre z.B. bei 1)
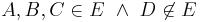 .
.
- Du hast eigentlich dastehen, dass
 überhaupt zusammen in irgendeiner Ebene liegen. Und das ist bei bis zu drei Punkten immer der Fall. Also, du hast die Komplanarität falsch verwendet.
überhaupt zusammen in irgendeiner Ebene liegen. Und das ist bei bis zu drei Punkten immer der Fall. Also, du hast die Komplanarität falsch verwendet.
- --Sternchen 18:52, 7. Jun. 2010 (UTC)
@ Sternchen
Aber es ist doch in der Bedingung gegeben, dass die Ebene  beliebig sei, also versuche ich die Punkte und die Relation derer in Bezug auf die Ebene zu klassifizieren. Das mache ich durch die Relation kollinear, weil wir diese definieren können. Also gibt es den Fall, dass drei Punkte kollinear sind (dann sind alle vier Punkte in einer Ebene. Oder es sind maximal zwei Punkte kollinear, dann sind mindestens drei Punkte komplanar.
Die von Gänseblümchen aufgelisteten Fälle 2 und 3 existieren ja nicht, also dass in einer beliebigen Ebene nur ein Punkt liegt geht ja nicht, anders ausgedrückt, dass es eine Ebene gibt, in der mindestens drei Punkte liegen! Wenn wir den Fall 1 und 4 anschauen, so sind das ja genau die Fälle (o.B.d.A), die oben aufgelistet wurden als
beliebig sei, also versuche ich die Punkte und die Relation derer in Bezug auf die Ebene zu klassifizieren. Das mache ich durch die Relation kollinear, weil wir diese definieren können. Also gibt es den Fall, dass drei Punkte kollinear sind (dann sind alle vier Punkte in einer Ebene. Oder es sind maximal zwei Punkte kollinear, dann sind mindestens drei Punkte komplanar.
Die von Gänseblümchen aufgelisteten Fälle 2 und 3 existieren ja nicht, also dass in einer beliebigen Ebene nur ein Punkt liegt geht ja nicht, anders ausgedrückt, dass es eine Ebene gibt, in der mindestens drei Punkte liegen! Wenn wir den Fall 1 und 4 anschauen, so sind das ja genau die Fälle (o.B.d.A), die oben aufgelistet wurden als  1 bis
1 bis  3.
3.
Wenn man nun beliebig so auslegt, dass jedwede Relation zu den Punkten möglich ist, so haben wir auch die Fälle, dass die Ebene durch keinen oder durch einen oder durch zwei Punkte geht. Aber das ist doch die Gesamtheit aller Ebenen, dann hab ich die Fragestellung falsch verstanden, denn diese Auflistung ist doch trivial, oder...?
--Heinzvaneugen
- Jetzt, wo du es sagst, kommt es mir auch so vor, dass die Auflistung der Fälle, die ich gemeint habe, recht trivial ist. Ich weiß jetzt auch nicht so recht, ob ich die Fragestellung richtig verstanden habe. Und ich bin übrigens tatsächlich von der Gesamtheit aller Ebenen ausgegangen, das steckt für mich in dem Wort "beliebig", für dich nicht?
- Ich kann deine Überlegungen nicht durchdringen und stelle deshalb mal ein paar Fragen:
- Warum kann es nicht sein, dass in einer beliebigen Ebene nur einer von unseren Punkten liegt?
- Warum kann es nicht sein, dass es eine Ebene gibt, in der drei Punkte liegen?
- Was hat 1. mit 2. zu tun?
- --Sternchen 18:52, 7. Jun. 2010 (UTC)

