Lösung von Aufgabe 12.2: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
 
(6 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 7: Zeile 7:
 
Definition spitzer Winkel: Ein spitzer Winkel ist kleiner als ein rechter Winkel. Definition korrekt? (Diskussion)
 
Definition spitzer Winkel: Ein spitzer Winkel ist kleiner als ein rechter Winkel. Definition korrekt? (Diskussion)
 
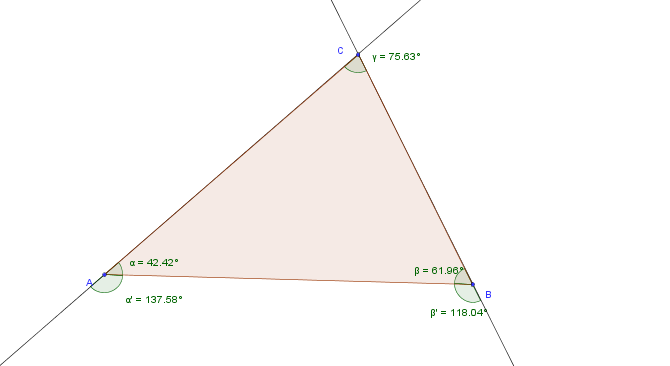
<br />Voraussetzung: Dreieck <math>\overline {ABC}</math>
 
<br />Voraussetzung: Dreieck <math>\overline {ABC}</math>
−
<br />Behauptung: o.B.d.A: <math>|\angle BAC| < 90</math> und <math>|\angle ABC| < 90</math>
+
<br />Behauptung:
−
<br />Der Einfachheit halber werden die Winkel mit <math>\alpha \ \beta \ \gamma</math> bezeichnet, die jeweiligen Außenwinkel sind dann <math>\alpha' \ \beta' \ \gamma'</math>
+
<br />Der Einfachheit halber werden die Winkel mit <math>\alpha \ \beta \ \gamma</math> bezeichnet, die jeweiligen Außenwinkel sind dann <math>\alpha' \ \beta' \ \gamma'</math>. Es gilt entweder....
−
<br />Behauptung:
+
::(1) <math>|\alpha| \ < 90 \land |\beta| \ < 90</math>  
−
::(1) <math>|\alpha| \ < 90</math> und <math>|\beta| \ < 90</math>  
+
::oder (2) <math>|\beta| \ < 90 \land |\gamma| \ < 90</math>
−
::oder (2) <math>|\alpha| \ < 90</math> und <math>|\gamma| \ < 90</math>  
+
::oder (3) <math>|\alpha| \ < 90 \land |\gamma| \ < 90</math>  
−
::oder (3) <math>|\beta| \ < 90</math> und <math>|\gamma| \ < 90</math>
+
<br />Indirekter Beweis.
 +
<br />Annahme: Es gilt entweder....
 +
::(1) <math>|\alpha| \ \ge 90 \land |\beta| \ \ge 90</math>  
 +
::oder (2) <math>|\beta| \ \ge 90 \land |\gamma| \ \ge 90</math>
 +
::oder (3) <math>|\alpha| \ \ge 90 \land |\gamma| \ \ge 90</math>
 +
Anmerkung: Man muss natürlich aus <math>\ < </math>in der Behauptung <math>\ \ge</math> in der Annahme machen, denn spitze Winkel sind KLEINER ALS rechte Winkel. Rechte Winkel selbst zählen somit nicht zur möglichen Menge der spitzen Winkel. In der zu widerlegenden Annahme geht man somit von allen möglichen Fällen aus, also auch von dem Fall, dass zwei rechte Winkel in einem Dreieck möglich sind. Somit ist eine Umformulierung des Korollars: "In jedem Dreieck gibt es höchstens einen rechten Winkel." Dies wird durch den Beweis gleich mit bewiesen! (Oder doch nicht? --> Diskussion)
 
<br />[[Bild:Skizze_Übung_12_2.png]]
 
<br />[[Bild:Skizze_Übung_12_2.png]]
 
{| class="wikitable "
 
{| class="wikitable "
Zeile 20: Zeile 25:
 
|-
 
|-
 
! style="background: #FFDDDD;"|(I)
 
! style="background: #FFDDDD;"|(I)
−
|  
+
| Es gilt: <math>|\alpha| \ < |\beta'|</math> und <math>|\gamma| \ < |\beta'|</math>
−
|  
+
| schwacher Außenwinkelsatz
 
|-
 
|-
 
! style="background: #FFDDDD;"|(II)
 
! style="background: #FFDDDD;"|(II)
−
|  
+
| <math>|\beta| \ + |\beta'| = 180</math>
−
|  
+
| Axiom IV.4: (Supplementaxiom): Nebenwinkel sind supplementär.
 
|-
 
|-
 
! style="background: #FFDDDD;"|(III)
 
! style="background: #FFDDDD;"|(III)
−
|  
+
| <math>\ |\beta'| = 180 - |\beta|</math>
−
|  
+
| (II) Algebraische Umformung
 
|-
 
|-
 
! style="background: #FFDDDD;"|(IV)
 
! style="background: #FFDDDD;"|(IV)
−
|  
+
| <math>|\alpha| \ < 180 - |\beta|</math> und <math>|\gamma| \ < 180 - |\beta|</math>
−
|  
+
| (I), (III)
 +
|-
 +
! style="background: #FFDDDD;"|(V)
 +
| <math>|\alpha| + |\beta|\ < 180 </math> und <math>|\gamma| + |\beta| \ < 180</math>
 +
| (IV) Algebraische Umformung
 
|-
 
|-
 
! style="background: #FFDDDD;"|(VI)
 
! style="background: #FFDDDD;"|(VI)
−
|  
+
| Wenn <math>|\alpha| + |\beta|\ < 180 </math> gilt, muss (1) <math>|\alpha| \ \ge 90</math> und <math>|\beta| \ \ge 90</math> verworfen werden.
−
|
+
| Annahme, (V)
 
|-
 
|-
 
! style="background: #FFDDDD;"|(VII)
 
! style="background: #FFDDDD;"|(VII)
−
|  
+
| Wenn <math>|\gamma| + |\beta| \ < 180</math> gilt, muss (2) <math>|\beta| \ \ge 90</math> und <math>|\gamma| \ \ge 90</math> verworfen werden.
−
|  
+
| Annahme, (V)
 
|-
 
|-
 
! style="background: #FFDDDD;"|(VIII)
 
! style="background: #FFDDDD;"|(VIII)
−
|  
+
| Es gilt: <math>|\beta| \ < |\alpha'|</math> und <math>|\gamma| \ < |\alpha'|</math>
−
|  
+
| schwacher Außenwinkelsatz
 
|-
 
|-
 
! style="background: #FFDDDD;"|(IX)
 
! style="background: #FFDDDD;"|(IX)
−
|  
+
| Wenn <math>|\alpha| + |\gamma| \ < 180</math> gilt, muss (3) <math>|\alpha| \ \ge 90</math> und <math>|\gamma| \ \ge 90</math> verworfen werden.
−
|  
+
| Beweis zusammengefasst, analog zu Schritte (I) bis (VII)
−
|-
+
−
! style="background: #FFDDDD;"|(X)
+
−
|
+
−
|  
+
 
|}
 
|}
−
--[[Benutzer:Heinzvaneugen|Heinzvaneugen]] 21:48, 11. Jul. 2010 (UTC)
+
<br />Annahme muss verworfen werden.
 +
<br />--[[Benutzer:Heinzvaneugen|Heinzvaneugen]] 21:48, 11. Jul. 2010 (UTC)
 +
 
 +
 
 +
Versuch:
 +
 
 +
Voraussetzung: Es sei ein Dreierck <math>\overline {ABC}</math><br />
 +
Behauptung: es seien mindesten zwei Innenwinkel spitze Winkel<br />
 +
 
 +
Annahme: es sei höchsten ein Winkel ein spitzer Winkel<br /><br />
 +
 
 +
alpha < 90 nach Definition Spitzer Winkel
 +
somit sind beta und gamma beide größer gleich 90 (Maß) nach Annahme
 +
 
 +
so bleiben für schwachen Winkelsatz die Möglichkeiten:
 +
 
 +
beta + beta' aus dem folgt entweder ist beta > bata' oder |beta = beta'
 +
analog gilt das auch für gamma nach Komplementäraxiom Nebenwinkel.
 +
 
 +
zu müsste es doch zum Widerspruch kommen oder??? nach schwachen Außenwinkelsatz?????
 +
 
 +
 
 +
* Kann man das nicht einfach über die Winkelsumme im Dreieck beweisen, oder darf man das hier nicht? --[[Benutzer:Schmarn|Schmarn]] 22:03, 12. Jan. 2012 (CET)

Aktuelle Version vom 12. Januar 2012, 22:03 Uhr

Aufgabenstellung

Beweisen Sie:
Korollar 1 zum schwachen Außenwinkelsatz

In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel.

Lösung 1

Definition spitzer Winkel: Ein spitzer Winkel ist kleiner als ein rechter Winkel. Definition korrekt? (Diskussion)
Voraussetzung: Dreieck \overline {ABC}
Behauptung:
Der Einfachheit halber werden die Winkel mit 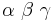\alpha \ \beta \ \gamma bezeichnet, die jeweiligen Außenwinkel sind dann 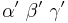\alpha' \ \beta' \ \gamma'. Es gilt entweder....

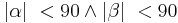
(1) |\alpha| \ < 90 \land |\beta| \ < 90
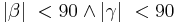
oder (2) |\beta| \ < 90 \land |\gamma| \ < 90
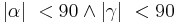
oder (3) |\alpha| \ < 90 \land |\gamma| \ < 90


Indirekter Beweis.
Annahme: Es gilt entweder....

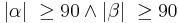
(1) |\alpha| \ \ge 90 \land |\beta| \ \ge 90
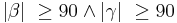
oder (2) |\beta| \ \ge 90 \land |\gamma| \ \ge 90
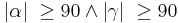
oder (3) |\alpha| \ \ge 90 \land |\gamma| \ \ge 90

Anmerkung: Man muss natürlich aus 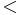\ < in der Behauptung 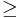\ \ge in der Annahme machen, denn spitze Winkel sind KLEINER ALS rechte Winkel. Rechte Winkel selbst zählen somit nicht zur möglichen Menge der spitzen Winkel. In der zu widerlegenden Annahme geht man somit von allen möglichen Fällen aus, also auch von dem Fall, dass zwei rechte Winkel in einem Dreieck möglich sind. Somit ist eine Umformulierung des Korollars: "In jedem Dreieck gibt es höchstens einen rechten Winkel." Dies wird durch den Beweis gleich mit bewiesen! (Oder doch nicht? --> Diskussion)
Skizze Übung 12 2.png

Nr. Beweisschritt Begründung
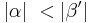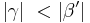
(I) Es gilt: |\alpha| \ < |\beta'| und |\gamma| \ < |\beta'| schwacher Außenwinkelsatz
(II) |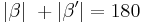\beta| \ + |\beta'| = 180 Axiom IV.4: (Supplementaxiom): Nebenwinkel sind supplementär.
(III) 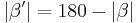\ |\beta'| = 180 - |\beta| (II) Algebraische Umformung
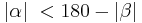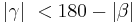
(IV) |\alpha| \ < 180 - |\beta| und |\gamma| \ < 180 - |\beta| (I), (III)
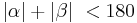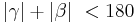
(V) |\alpha| + |\beta|\ < 180 und |\gamma| + |\beta| \ < 180 (IV) Algebraische Umformung
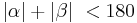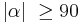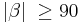(VI) Wenn |\alpha| + |\beta|\ < 180 gilt, muss (1) |\alpha| \ \ge 90 und |\beta| \ \ge 90 verworfen werden. Annahme, (V)
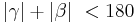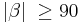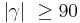(VII) Wenn |\gamma| + |\beta| \ < 180 gilt, muss (2) |\beta| \ \ge 90 und |\gamma| \ \ge 90 verworfen werden. Annahme, (V)
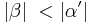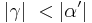
(VIII) Es gilt: |\beta| \ < |\alpha'| und |\gamma| \ < |\alpha'| schwacher Außenwinkelsatz
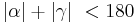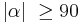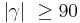(IX) Wenn |\alpha| + |\gamma| \ < 180 gilt, muss (3) |\alpha| \ \ge 90 und |\gamma| \ \ge 90 verworfen werden. Beweis zusammengefasst, analog zu Schritte (I) bis (VII)


Annahme muss verworfen werden.
--Heinzvaneugen 21:48, 11. Jul. 2010 (UTC)


Versuch:

Voraussetzung: Es sei ein Dreierck \overline {ABC}
Behauptung: es seien mindesten zwei Innenwinkel spitze Winkel

Annahme: es sei höchsten ein Winkel ein spitzer Winkel

alpha < 90 nach Definition Spitzer Winkel somit sind beta und gamma beide größer gleich 90 (Maß) nach Annahme

so bleiben für schwachen Winkelsatz die Möglichkeiten:

beta + beta' aus dem folgt entweder ist beta > bata' oder |beta = beta' analog gilt das auch für gamma nach Komplementäraxiom Nebenwinkel.

zu müsste es doch zum Widerspruch kommen oder??? nach schwachen Außenwinkelsatz?????


  • Kann man das nicht einfach über die Winkelsumme im Dreieck beweisen, oder darf man das hier nicht? --Schmarn 22:03, 12. Jan. 2012 (CET)
Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_12.2&oldid=10512“