Klippenspringer: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
|||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Die Klippenspringer von Acapulco (Mexiko) legen eine | + | Die Klippenspringer von Acapulco (Mexiko) legen eine parabelförmige Flugbahn zurück, die sich mit der Gleichung <math>y=-x^2+28</math>(<math>x</math> und <math>y</math> in Metern) beschreiben lässt. |
a) Wie weit entfernt vom Fuß des Felsens taucht der Springer ins Wasser? | a) Wie weit entfernt vom Fuß des Felsens taucht der Springer ins Wasser? | ||
| − | b) Der Fels ist 27 m hoch. Erkläre die | + | b) Der Fels ist 27 m hoch. Erkläre die Parabelgleichung. |
(aus: Schnittpunkt Mathematik 6, Klett, S.63) | (aus: Schnittpunkt Mathematik 6, Klett, S.63) | ||
Aktuelle Version vom 19. Januar 2012, 13:13 Uhr
Die Klippenspringer von Acapulco (Mexiko) legen eine parabelförmige Flugbahn zurück, die sich mit der Gleichung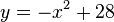 
(
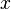und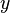 
in Metern) beschreiben lässt.
a) Wie weit entfernt vom Fuß des Felsens taucht der Springer ins Wasser?
b) Der Fels ist 27 m hoch. Erkläre die Parabelgleichung.
(aus: Schnittpunkt Mathematik 6, Klett, S.63)
