Strahlensätze (2011/12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
HecklF (Diskussion | Beiträge) (→Beweis der Inkommensurabilität von Quadratseite und -diagonale) |
*m.g.* (Diskussion | Beiträge) (→Satz II.03: Inkommensurabilität von Quadratseite und Quadratdiagonale) |
||
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Strahlensätze== | ==Strahlensätze== | ||
| − | ===1. Strahlensatz (STS I)=== | + | ===Satz II.04: 1. Strahlensatz (STS I)=== |
Seien a und b zwei Strahlen aus einem Büschel mit dem gemeinsamen Punkt A. Ferner seien g und h zwei parallele Gerade, die mit a und b jeweils genau einen gemeinsamen Punkt haben.<br /> | Seien a und b zwei Strahlen aus einem Büschel mit dem gemeinsamen Punkt A. Ferner seien g und h zwei parallele Gerade, die mit a und b jeweils genau einen gemeinsamen Punkt haben.<br /> | ||
Das Verhältnis zweier Strahlenabschnitte des Strahls a ist identisch dem Verhältnis der zwei gleichliegenden Strahlenabschnitte des Strahls b. Gleichliegende Strahlenabschnitte sind dabei Abschnitte von verschiedenen Strahlen, die jeweils zwischen dem Scheitelpunkt A und derselben Parallele oder zwischen den gleichen Parallelen liegen.<br /> --[[Benutzer:HecklF|Flo60]] 13:03, 18. Jan. 2012 (CET) | Das Verhältnis zweier Strahlenabschnitte des Strahls a ist identisch dem Verhältnis der zwei gleichliegenden Strahlenabschnitte des Strahls b. Gleichliegende Strahlenabschnitte sind dabei Abschnitte von verschiedenen Strahlen, die jeweils zwischen dem Scheitelpunkt A und derselben Parallele oder zwischen den gleichen Parallelen liegen.<br /> --[[Benutzer:HecklF|Flo60]] 13:03, 18. Jan. 2012 (CET) | ||
| − | ===Beweis: AB | + | ===Beweis : <math>\frac{|AB|}{|BC|}=\frac{|AB'|}{|BC'|}</math>=== |
Bei allen Beweisen wird hier das Problem der Kommensurabilität auftauchen. Dieses lagern wir jedoch aus!<br /><br /> | Bei allen Beweisen wird hier das Problem der Kommensurabilität auftauchen. Dieses lagern wir jedoch aus!<br /><br /> | ||
<ggb_applet width="1366" height="607" version="4.0" ggbBase64="UEsDBBQACAAIACpoMkAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAAqaDJAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1cW2/cRpZ+zvyK2l4jmAEsqu4XjZTAUuxEgOMEsNczWAgw2M1SNyM22SHZunhn3md+wj7NS35DnvZN/2R+yZ6qIvsupVu3aY1huUhWsS7nnO87p05R3v/6cpihc1tWaZEfdEiEO8jmvSJJ8/5BZ1yf7ujO11/9br9vi77tljE6LcphXB90uGuZJgcdyxXlnIkdaona4QZ3d7pS8h1BdCysFarLTQehyyrdy4t38dBWo7hn3/cGdhi/LXpx7Qce1PVob3f34uIiaoeKirK/2+93o8sq6SCYZl4ddJqLPehu7qUL5ptTjMnun79/G7rfSfOqjvOe7SC3hHH61e++2L9I86S4QBdpUg9gwUzTDhrYtD+ARSnOO2jXtRqBREa2V6fntoJ3Z279ouvhqOObxbmr/yJcoWyyng5K0vM0seVBB0dEcaa54YZxraTRII+iTG1eN41JM+hu293+eWovQr/uyg8JM6uLIuvGrkv0l78giilGL11BQkGhkDJU4fAMs1DQUPBQiNCGh9d5aMpDGx7acNZB52mVdjN70DmNswpkmOanJehvcl/VV5n182keTJdPXsKaqvQzNGYYDCUIHZ5j/NL9SPjhrmJ3fpFkZtS6HG84aDskYVKuPya910pZOyjlZHlMKm5Yp7xl0LDwtRYqZmQLQ/m//mdpRHbbMhdHDPf3G1DyJ1ni/m6Llf0GHqgauLaN+dR2WDnAMIOEcXZPkABwSAVmLhAxUCiKAA6ICMQF3BKNpCsVYgoqOGJII9eOMOTRITT8w5XvTCIBnbmnCkCJCAzEkWCIeFBxBFBCHpgAUsqghRBIwEtueEJdF0wiLuGOacRhjg6TikBDBi/CPQxPESOIuZeJQlQi6foj3GFdajd16JIiiZEkrkOANUA6wBnaa8TcamQjrjQfjes5EfWGSXtZF6OJLqA1ENKU9wJBzdHiF/tZ3LUZuIr3TpMInceZQ4Qf6LTIa9QqkYZn/TIeDdJe9d7WNbxVoZ/i8/htXNvLN9C6asf2bXtFXv1YFvVRkY2HeYVQr8jwZM5FRmau6WTWcMNmKvhshZipkDPXauW4BdSgcWVh/KKs2uZxkhy7FlNqAEn+kGdXh6WNz0ZFOr+M/V3vdfbtuJelSRrnH8FY3ShOLmjqhBxftU5IKNPOpCiT91cVmDC6/G9bFiBbExkNLotTBa5ECyI66KqpIjJSBEhdKS6JkRjwV/Vihz6hIs4F9KukxESAs4a3bq7zg9vziZLiSztdb7904J65Oa4Oi2z6yIvgKB7V49KHEMCPpVvXq7yfWW8mnnHBP/fOusXl+4awQ18frkZwh8MMun0vegT0QAXMuN+U3VD6Nm5qk1bYt8G+BW4NLk0m9cRQ38KX3VD6VmDBYWrNUkm7TILbYdLKkxruNNBpCcvZv/P24zyt37Y3ddo7a5ZKwgvvxsOunVjRfJ/kofrc310ws/0zW+Y2a6walDkuxlUA6YzBJ7aXDuE2VDQiiZ26/gsmEJ4mtl/aduKZD8+CwHwtnrXXpce+qzdlMTzOzz+ALSxMYH+3neV+1SvTkbM51AVPcGanVpWkVQyOJJl9z8EQlt5zDgPEUzvRHNoLC2J9/+E9Ot5Drw73Do/QAZRfxqOi+iPaQ83VUSgAz+N6UIBtvMkKCcpNgItA2g6xmR1ChIZqb5LeqieqeeVjP6cDVHR/AjqceMxQP1UyVK80T2/IcTYaxC4+bASVxVe2nBOd7+/7IlkUKOjLrxqoYeQDTLCIkbXBmMKM4WIEHXoMzrEb6KhCly7UF0A6VwedHRxBQPo5BP8h+HWrdcicI/TwdEG9YHNBUL8hso/LIps392chMxPhicyYfhCh9YrhMM4TlPu46C0wUWfqpmPsjA3FxAkwCGdctxVx6KrpYEn+jtQm0o1/w2JnVnuT+PHdhT8VIMhNUC9BFQkvPyglIWb6Ryxycg0RwxnsiyrvOOrGRfiL79IksT5aDD7r5zy8UgWiTIejLO2l9SaGerhd2L6LlYpIwb4DMyUkhAK4MVkwVNiKUS0EodJII/iT2u/hkv12N7Df7rbYL4nMvBSZFy6PiJwVufKyhYBMwJ5fGUqwoISRxzfteXX86E17Xh/dJUUc3a6IeXwc3QkfhIYAzpfbgBGIegUB3qEKE8UEbzGiqdFGMoK1lvDnYTj+Nnl+v118cze/yCMJglOcMcGUYtQ00lREww1mUimqpWP+p2Ccw8A43y8Zem8DxultC+NgkK0GzuHAORg2eUaHCATEyCmmhgOxSO0k7KUrIkyY5tRQLOAVyp+ac1Yo5CgopLekkGQDhSTPVCEK/K7ghGtwAeAhtHpqhRznNWwTQWALWukFrcRLWmn2SJt4hfaVu3CZSxT2Q9ENxf2VxEXENdWEK8mNBF0EFdFIGEWUYYQygAlzWW6PGYU5UL7hoB9AjXxAfrpJ+slN0j/aXPpHWyZ9CRDhEAYxbQyARPEWIIILI4lhlGrKpFCPLv0fi+yqX+SrQ9JpEoCuik8/ptBr74yExt1PJDSM/QUD/KynqDCByT647fSuHLAWAfaKPEmDV3fpyaZ1iv7593+g1WYgiDcDVyyFFGQTO7g57qls391NY/pPZH1Kf9gV3Yv8qTaKGU0xgb/Em7aJMNAKhycCoknKAvObiHChpAAnLAyXXD8O83ujzVx0NuEakNNynu/M2pFLsP6QfyjjvHIHuaHNTP5wTdXFz1F1JALOh6BISENBLZqLQEs8MlgqJsFpc6oolSFKBV+BqaRYcwM6pHQpV/xstddby11snwZv2HvvrN587zzR7vtRFLiJF2v819QbrfJitPFisy4v/kQbT/aJ3MmL0S31Yu0xkbt9dC/2ZGBauaq70yGN1HyuI8TIItJmNjEiROPLhMQS7rQmzLDlk7MtBtNv+TL67JRHI2BBoDShXeocdjledS63Dp6NuVhDMXBnQXU7RLlDY4hDQNFEQOD97xOI9J4kEHlY5eGIw+ZIQ6hhpFaCGNkEIjLihEnYHREpuQS1tn6MSwluD/wdNVyJR8roPI72LkclTMzJvNHHB3tZgxih4qDz5c/jov7j6wr106xGn8fos037Nt9DL06Kc1u6Ff7Pq8O/ohO0h6ZPDo/ckwP4mW0VaHip7dxx71/DgH6S83ZVw6w681O8U7bpAeOetHobf7B/npdt81lNZcv0dPIVVfiEQnZarbY+to7L2p8AoMAZEMwKrQxEtAziXc4avseSSqIVgQiKY4nFbJL25pjkh7IeFBATxNmqDOwkzJiJORYjE7tB8s/+1vHxk2X/GIskBuKV2CitALANeImIhCKSCgdTwUw4UqcSR1pwKaSLXOXW5P66t6vmm02yT99sTd7pXfzOK8OXn0P5+Jk828hySYqvN5Hi67WluNqNZbe4sceQNQQe7nzHuSbYiunmyIcqGTEC4IBdNhamPT9TMBChiguIKalwn6Y9nFreNyHBLQz0ekk1p7erZjHMOH1E5bTftjU+Y4MY44fT08rWIbcRzi/lSt2xFbE/1qAeDRQGjA9bgMmHQBIYjXLtPiAAjmvUJyMiiMtwaSGdm5C30JiYHBqKf10IAouNR14L/vGLwaeZkKCNCdooYvCJvriPr5vmhxetrL+Bh+tvjYdbkcy8Wp35dMl7GgnYW2DANpiRfvLTxptIud98NdWm2xdV8ybUf7sJRb95ZhQNW3mmIRbBjBiugXonisSMKQ4a44JI3ByCPeZHDt9uTYiw5rdRj/Glwg2OKhjimyULHWzmogZb7qJooBG2posikWSwHQGtKEUJdZ8FhhQHcf7JUCXcrz8RTIOmgLS4VFprxikTjLHbviJ8Pi5quqkNjoosOap5o+gWRWbjaZ429UYBA4zt0gzv88nR+o5magCEhRCRU3MrVGel8l2anVp0vF5Wgc5lFV6gV+PTfjkG+J2gBKZ2nJ8V8H41LuNumqX19S811JxDHyfo7fUved+6q7RyT23qrqGD2qaZf/7iy/8kGDqdax93q94gT+vaN8nT3sC9nA6HMNwJGl7/2ge7GUST15s+PoKa474t3UsXqWuapLayFVz8WBZdWKZ7FJ9e/5+ry+PeAIp4fP2PuZn8Pokn7+fjPPQyt5Z6YIvS1mnlO2inNwTJ+eqz61/z3OZ/iKDLtfMij5orfaBYZsPMCZ4kTvDKxAnhkcubamPcxz0ca9V88im1VoZASMwk+BN6U97kdoj+tE0QNS1E9aYQXROjbAGjf/LmG9J+7mKcX//SG1T1S4+AqppYNSCyb6Ed4M0GuH1T2hRCO1d5VuSAdCfjE9BpnkQTkCxnCH06MaC8LtPzNM5s6X5nZLGfz2PfmYdOZbNuVUfzKH419nVhetPJ3EbiJyjQ0XJ+0s/KTX12Fv8BN3+Ky/Hwa7h4A5VeEE4mA1vGY3dRJJ5qghJOQA3H0Qu0PprZfdH80/NDM4mEMlowQiAAphAch8RFxDXshSEslka5365jd4Pz2RbBmUp+ZziviWe+iGfwl2CHXZsm87BocPKtc8iVTWs7D4OZ9H08PvV4nPV1jRf3XUDPufdp7ua761996ZA4gGnlLyftEu9GX3Xd/wDQxgDgYOMyzjIbnDp0VI1K5xc38oH8vqg5e36oYRGHjaRzfpIzQ8zk16CEpoxiwSQlRAph7gabbItgwxi+K2w+brbq4RatWjSuX6y/6LfXv1bjvL8eU4gFpnjt3Jc799sDh9VEtMd/2EP4pQg5OfTPv/3vylM/aHGC3GZoscWCv50Eyse39RvOF2/rd3q22Pb4LoTkoWOYtXPace4YpW/PIGr/7AKIC1smnmUa8goNILpPu/WEpA7tIHZb/rwfrc8/4r78M3x+/BMpLCkwj9FSSCXaX8OkkaCGSEMp4Yool5q+gX92Z39d2P9ifvPfzHz1/1BLBwjQ7JCeWA4AAANHAABQSwECFAAUAAgACAAqaDJARczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIACpoMkDQ7JCeWA4AAANHAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAA8A4AAAAA" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | <ggb_applet width="1366" height="607" version="4.0" ggbBase64="UEsDBBQACAAIACpoMkAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAAqaDJAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1cW2/cRpZ+zvyK2l4jmAEsqu4XjZTAUuxEgOMEsNczWAgw2M1SNyM22SHZunhn3md+wj7NS35DnvZN/2R+yZ6qIvsupVu3aY1huUhWsS7nnO87p05R3v/6cpihc1tWaZEfdEiEO8jmvSJJ8/5BZ1yf7ujO11/9br9vi77tljE6LcphXB90uGuZJgcdyxXlnIkdaona4QZ3d7pS8h1BdCysFarLTQehyyrdy4t38dBWo7hn3/cGdhi/LXpx7Qce1PVob3f34uIiaoeKirK/2+93o8sq6SCYZl4ddJqLPehu7qUL5ptTjMnun79/G7rfSfOqjvOe7SC3hHH61e++2L9I86S4QBdpUg9gwUzTDhrYtD+ARSnOO2jXtRqBREa2V6fntoJ3Z279ouvhqOObxbmr/yJcoWyyng5K0vM0seVBB0dEcaa54YZxraTRII+iTG1eN41JM+hu293+eWovQr/uyg8JM6uLIuvGrkv0l78giilGL11BQkGhkDJU4fAMs1DQUPBQiNCGh9d5aMpDGx7acNZB52mVdjN70DmNswpkmOanJehvcl/VV5n182keTJdPXsKaqvQzNGYYDCUIHZ5j/NL9SPjhrmJ3fpFkZtS6HG84aDskYVKuPya910pZOyjlZHlMKm5Yp7xl0LDwtRYqZmQLQ/m//mdpRHbbMhdHDPf3G1DyJ1ni/m6Llf0GHqgauLaN+dR2WDnAMIOEcXZPkABwSAVmLhAxUCiKAA6ICMQF3BKNpCsVYgoqOGJII9eOMOTRITT8w5XvTCIBnbmnCkCJCAzEkWCIeFBxBFBCHpgAUsqghRBIwEtueEJdF0wiLuGOacRhjg6TikBDBi/CPQxPESOIuZeJQlQi6foj3GFdajd16JIiiZEkrkOANUA6wBnaa8TcamQjrjQfjes5EfWGSXtZF6OJLqA1ENKU9wJBzdHiF/tZ3LUZuIr3TpMInceZQ4Qf6LTIa9QqkYZn/TIeDdJe9d7WNbxVoZ/i8/htXNvLN9C6asf2bXtFXv1YFvVRkY2HeYVQr8jwZM5FRmau6WTWcMNmKvhshZipkDPXauW4BdSgcWVh/KKs2uZxkhy7FlNqAEn+kGdXh6WNz0ZFOr+M/V3vdfbtuJelSRrnH8FY3ShOLmjqhBxftU5IKNPOpCiT91cVmDC6/G9bFiBbExkNLotTBa5ECyI66KqpIjJSBEhdKS6JkRjwV/Vihz6hIs4F9KukxESAs4a3bq7zg9vziZLiSztdb7904J65Oa4Oi2z6yIvgKB7V49KHEMCPpVvXq7yfWW8mnnHBP/fOusXl+4awQ18frkZwh8MMun0vegT0QAXMuN+U3VD6Nm5qk1bYt8G+BW4NLk0m9cRQ38KX3VD6VmDBYWrNUkm7TILbYdLKkxruNNBpCcvZv/P24zyt37Y3ddo7a5ZKwgvvxsOunVjRfJ/kofrc310ws/0zW+Y2a6walDkuxlUA6YzBJ7aXDuE2VDQiiZ26/gsmEJ4mtl/aduKZD8+CwHwtnrXXpce+qzdlMTzOzz+ALSxMYH+3neV+1SvTkbM51AVPcGanVpWkVQyOJJl9z8EQlt5zDgPEUzvRHNoLC2J9/+E9Ot5Drw73Do/QAZRfxqOi+iPaQ83VUSgAz+N6UIBtvMkKCcpNgItA2g6xmR1ChIZqb5LeqieqeeVjP6cDVHR/AjqceMxQP1UyVK80T2/IcTYaxC4+bASVxVe2nBOd7+/7IlkUKOjLrxqoYeQDTLCIkbXBmMKM4WIEHXoMzrEb6KhCly7UF0A6VwedHRxBQPo5BP8h+HWrdcicI/TwdEG9YHNBUL8hso/LIps392chMxPhicyYfhCh9YrhMM4TlPu46C0wUWfqpmPsjA3FxAkwCGdctxVx6KrpYEn+jtQm0o1/w2JnVnuT+PHdhT8VIMhNUC9BFQkvPyglIWb6Ryxycg0RwxnsiyrvOOrGRfiL79IksT5aDD7r5zy8UgWiTIejLO2l9SaGerhd2L6LlYpIwb4DMyUkhAK4MVkwVNiKUS0EodJII/iT2u/hkv12N7Df7rbYL4nMvBSZFy6PiJwVufKyhYBMwJ5fGUqwoISRxzfteXX86E17Xh/dJUUc3a6IeXwc3QkfhIYAzpfbgBGIegUB3qEKE8UEbzGiqdFGMoK1lvDnYTj+Nnl+v118cze/yCMJglOcMcGUYtQ00lREww1mUimqpWP+p2Ccw8A43y8Zem8DxultC+NgkK0GzuHAORg2eUaHCATEyCmmhgOxSO0k7KUrIkyY5tRQLOAVyp+ac1Yo5CgopLekkGQDhSTPVCEK/K7ghGtwAeAhtHpqhRznNWwTQWALWukFrcRLWmn2SJt4hfaVu3CZSxT2Q9ENxf2VxEXENdWEK8mNBF0EFdFIGEWUYYQygAlzWW6PGYU5UL7hoB9AjXxAfrpJ+slN0j/aXPpHWyZ9CRDhEAYxbQyARPEWIIILI4lhlGrKpFCPLv0fi+yqX+SrQ9JpEoCuik8/ptBr74yExt1PJDSM/QUD/KynqDCByT647fSuHLAWAfaKPEmDV3fpyaZ1iv7593+g1WYgiDcDVyyFFGQTO7g57qls391NY/pPZH1Kf9gV3Yv8qTaKGU0xgb/Em7aJMNAKhycCoknKAvObiHChpAAnLAyXXD8O83ujzVx0NuEakNNynu/M2pFLsP6QfyjjvHIHuaHNTP5wTdXFz1F1JALOh6BISENBLZqLQEs8MlgqJsFpc6oolSFKBV+BqaRYcwM6pHQpV/xstddby11snwZv2HvvrN587zzR7vtRFLiJF2v819QbrfJitPFisy4v/kQbT/aJ3MmL0S31Yu0xkbt9dC/2ZGBauaq70yGN1HyuI8TIItJmNjEiROPLhMQS7rQmzLDlk7MtBtNv+TL67JRHI2BBoDShXeocdjledS63Dp6NuVhDMXBnQXU7RLlDY4hDQNFEQOD97xOI9J4kEHlY5eGIw+ZIQ6hhpFaCGNkEIjLihEnYHREpuQS1tn6MSwluD/wdNVyJR8roPI72LkclTMzJvNHHB3tZgxih4qDz5c/jov7j6wr106xGn8fos037Nt9DL06Kc1u6Ff7Pq8O/ohO0h6ZPDo/ckwP4mW0VaHip7dxx71/DgH6S83ZVw6w681O8U7bpAeOetHobf7B/npdt81lNZcv0dPIVVfiEQnZarbY+to7L2p8AoMAZEMwKrQxEtAziXc4avseSSqIVgQiKY4nFbJL25pjkh7IeFBATxNmqDOwkzJiJORYjE7tB8s/+1vHxk2X/GIskBuKV2CitALANeImIhCKSCgdTwUw4UqcSR1pwKaSLXOXW5P66t6vmm02yT99sTd7pXfzOK8OXn0P5+Jk828hySYqvN5Hi67WluNqNZbe4sceQNQQe7nzHuSbYiunmyIcqGTEC4IBdNhamPT9TMBChiguIKalwn6Y9nFreNyHBLQz0ekk1p7erZjHMOH1E5bTftjU+Y4MY44fT08rWIbcRzi/lSt2xFbE/1qAeDRQGjA9bgMmHQBIYjXLtPiAAjmvUJyMiiMtwaSGdm5C30JiYHBqKf10IAouNR14L/vGLwaeZkKCNCdooYvCJvriPr5vmhxetrL+Bh+tvjYdbkcy8Wp35dMl7GgnYW2DANpiRfvLTxptIud98NdWm2xdV8ybUf7sJRb95ZhQNW3mmIRbBjBiugXonisSMKQ4a44JI3ByCPeZHDt9uTYiw5rdRj/Glwg2OKhjimyULHWzmogZb7qJooBG2posikWSwHQGtKEUJdZ8FhhQHcf7JUCXcrz8RTIOmgLS4VFprxikTjLHbviJ8Pi5quqkNjoosOap5o+gWRWbjaZ429UYBA4zt0gzv88nR+o5magCEhRCRU3MrVGel8l2anVp0vF5Wgc5lFV6gV+PTfjkG+J2gBKZ2nJ8V8H41LuNumqX19S811JxDHyfo7fUved+6q7RyT23qrqGD2qaZf/7iy/8kGDqdax93q94gT+vaN8nT3sC9nA6HMNwJGl7/2ge7GUST15s+PoKa474t3UsXqWuapLayFVz8WBZdWKZ7FJ9e/5+ry+PeAIp4fP2PuZn8Pokn7+fjPPQyt5Z6YIvS1mnlO2inNwTJ+eqz61/z3OZ/iKDLtfMij5orfaBYZsPMCZ4kTvDKxAnhkcubamPcxz0ca9V88im1VoZASMwk+BN6U97kdoj+tE0QNS1E9aYQXROjbAGjf/LmG9J+7mKcX//SG1T1S4+AqppYNSCyb6Ed4M0GuH1T2hRCO1d5VuSAdCfjE9BpnkQTkCxnCH06MaC8LtPzNM5s6X5nZLGfz2PfmYdOZbNuVUfzKH419nVhetPJ3EbiJyjQ0XJ+0s/KTX12Fv8BN3+Ky/Hwa7h4A5VeEE4mA1vGY3dRJJ5qghJOQA3H0Qu0PprZfdH80/NDM4mEMlowQiAAphAch8RFxDXshSEslka5365jd4Pz2RbBmUp+ZziviWe+iGfwl2CHXZsm87BocPKtc8iVTWs7D4OZ9H08PvV4nPV1jRf3XUDPufdp7ua761996ZA4gGnlLyftEu9GX3Xd/wDQxgDgYOMyzjIbnDp0VI1K5xc38oH8vqg5e36oYRGHjaRzfpIzQ8zk16CEpoxiwSQlRAph7gabbItgwxi+K2w+brbq4RatWjSuX6y/6LfXv1bjvL8eU4gFpnjt3Jc799sDh9VEtMd/2EP4pQg5OfTPv/3vylM/aHGC3GZoscWCv50Eyse39RvOF2/rd3q22Pb4LoTkoWOYtXPace4YpW/PIGr/7AKIC1smnmUa8goNILpPu/WEpA7tIHZb/rwfrc8/4r78M3x+/BMpLCkwj9FSSCXaX8OkkaCGSEMp4Yool5q+gX92Z39d2P9ifvPfzHz1/1BLBwjQ7JCeWA4AAANHAABQSwECFAAUAAgACAAqaDJARczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIACpoMkDQ7JCeWA4AAANHAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAA8A4AAAAA" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| Zeile 14: | Zeile 14: | ||
<br /> --[[Benutzer:HecklF|Flo60]] 13:03, 18. Jan. 2012 (CET) | <br /> --[[Benutzer:HecklF|Flo60]] 13:03, 18. Jan. 2012 (CET) | ||
| − | ===2. Strahlensatz (STS 2)=== | + | ===Satz II.05: 2. Strahlensatz (STS 2)=== |
| − | ===3. Strahlensatz (STS 3)=== | + | ===Satz II.06: 3. Strahlensatz (STS 3)=== |
==Kommensurabilität== | ==Kommensurabilität== | ||
===Definition II.06=== | ===Definition II.06=== | ||
::Zwei Strecken <math>a</math> und <math>b</math> heißen genau dann kommensurabel, wenn es eine Strecke <math>m</math> und ganze Zahlen <math>p</math> und <math>q</math> derart gibt, dass <math>p|m|=|a|</math> und <math>q|m|=|b|</math> gilt. | ::Zwei Strecken <math>a</math> und <math>b</math> heißen genau dann kommensurabel, wenn es eine Strecke <math>m</math> und ganze Zahlen <math>p</math> und <math>q</math> derart gibt, dass <math>p|m|=|a|</math> und <math>q|m|=|b|</math> gilt. | ||
| − | ===Satz II. | + | ===Satz II.07: Inkommensurabilität von Quadratseite und Quadratdiagonale=== |
:: Die Seite <math>a</math> und die Diagonale <math>d</math> ein und desselben Quadrates sind nicht kommensurabel zueinander. | :: Die Seite <math>a</math> und die Diagonale <math>d</math> ein und desselben Quadrates sind nicht kommensurabel zueinander. | ||
Aktuelle Version vom 25. Januar 2012, 17:25 Uhr
Inhaltsverzeichnis |
Strahlensätze
Satz II.04: 1. Strahlensatz (STS I)
Seien a und b zwei Strahlen aus einem Büschel mit dem gemeinsamen Punkt A. Ferner seien g und h zwei parallele Gerade, die mit a und b jeweils genau einen gemeinsamen Punkt haben.
Das Verhältnis zweier Strahlenabschnitte des Strahls a ist identisch dem Verhältnis der zwei gleichliegenden Strahlenabschnitte des Strahls b. Gleichliegende Strahlenabschnitte sind dabei Abschnitte von verschiedenen Strahlen, die jeweils zwischen dem Scheitelpunkt A und derselben Parallele oder zwischen den gleichen Parallelen liegen.
--Flo60 13:03, 18. Jan. 2012 (CET)
Beweis : 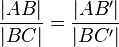
Bei allen Beweisen wird hier das Problem der Kommensurabilität auftauchen. Dieses lagern wir jedoch aus!
--Flo60 13:03, 18. Jan. 2012 (CET)
Beweis: AC : AB = AC' : AB'
--Flo60 13:03, 18. Jan. 2012 (CET)
Satz II.05: 2. Strahlensatz (STS 2)
Satz II.06: 3. Strahlensatz (STS 3)
Kommensurabilität
Definition II.06
- Zwei Strecken
 und
und  heißen genau dann kommensurabel, wenn es eine Strecke
heißen genau dann kommensurabel, wenn es eine Strecke  und ganze Zahlen
und ganze Zahlen  und
und 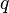 derart gibt, dass
derart gibt, dass 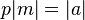 und
und 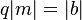 gilt.
gilt.
- Zwei Strecken
Satz II.07: Inkommensurabilität von Quadratseite und Quadratdiagonale
- Die Seite
 und die Diagonale
und die Diagonale  ein und desselben Quadrates sind nicht kommensurabel zueinander.
ein und desselben Quadrates sind nicht kommensurabel zueinander.
- Die Seite
Beweis der Inkommensurabilität von Quadratseite und -diagonale

