Definitionen in der Mathematik SoSe 12 S: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (Änderung 11457 von *m.g.* (Diskussion) rückgängig gemacht.) |
*m.g.* (Diskussion | Beiträge) (→Zurückführen auf bereits vorhanden Definitionen: Verwenden von Oberbegriffen) |
||
| (33 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{|width=90%| style="background-color:#FFFF99; padding:1em" | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| valign="top" | | | valign="top" | | ||
| − | == | + | ==Vorbemerkung== |
| + | Wenn im folgenden von Definitionen die Rede ist, dann im im Sinne einer mathematischen Definition. | ||
| + | ==Beispiele für Definitionen== | ||
===Begriffe, die im Satz des Thales verwendet werden=== | ===Begriffe, die im Satz des Thales verwendet werden=== | ||
| − | + | ====Der Satz des Thales==== | |
{| width="100%" | {| width="100%" | ||
| Zeile 11: | Zeile 13: | ||
<!-- linke Spalte: zwei div-Container --> | <!-- linke Spalte: zwei div-Container --> | ||
| width="50%" style="vertical-align:top; background-color:#FFFF99" | | | width="50%" style="vertical-align:top; background-color:#FFFF99" | | ||
| − | <div style="margin:0; margin-right: | + | <div style="margin:0; margin-right:4px; ; background-color:#FFFF99; align:left;"> |
| − | {|width=90%| style="background-color:#FFFF99; | + | {|width=90%| style="background-color:#FFFF99; " |
| valign="top" | | | valign="top" | | ||
| − | Einer der bekanntesten Sätze der Mathematik ist der Satz des Thales:<br /> | + | Einer der bekanntesten Sätze der Mathematik ist der Satz des Thales:<br /><br /> |
| − | ::Jeder Peripheriewinkel eine Kreises <math>k</math> über einem Durchmesser von <math>k</math> ist ein Rechter. | + | ::Jeder Peripheriewinkel eine Kreises <math>k</math> über einem Durchmesser von <math>k</math> ist ein Rechter.<br /><br /> |
| − | Man kann diesen Satz nicht verstehen geschweige denn beweisen, wenn man nicht weiß, was man unter den Begriffen ''Kreis'', ''Durchmesser'' und ''rechter Winkel'' versteht.<br /> | + | Man kann diesen Satz nicht verstehen, geschweige denn beweisen, wenn man nicht weiß, was man unter den Begriffen ''Kreis'', ''Durchmesser'' und ''rechter Winkel'' versteht.<br /><br /> |
| − | + | ||
|} | |} | ||
</div> | </div> | ||
<!-- rechte Spalte --> | <!-- rechte Spalte --> | ||
| width="50%" style="vertical-align:top" | | | width="50%" style="vertical-align:top" | | ||
| − | <div style="margin:0; margin-right:0px | + | <div style="margin:0; margin-right:0px;background-color:#FFFF99; align:left;"> |
| − | {|width=90%| style="background-color:#FFFF99 | + | {|width=90%| style="background-color:#FFFF99" |
| valign="top" | | | valign="top" | | ||
<ggb_applet width="303" height="336" version="4.0" ggbBase64="UEsDBBQACAAIAE9Hj0AAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAE9Hj0AAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1VnbjuM2En2efAUhBPs0lkmRus3aE7gbCHaAnswg3QmCfaMk2mYsS45I3xr5qfzIftMWScmW3T3evgw2iZEeimSxilWnblJG3+2WJdqIRsm6GnvExx4SVV4XspqNvbWeDhLvu/ffjGainoms4WhaN0uuxx4zlLIYe0GWh3QapwMRJtMBK7JwkKUZHRQRw0HGw1AUuYfQTsl3Vf0DXwq14rm4zediyW/qnGsreK716t1wuN1u/U6UXzez4WyW+TtVeAiuWamx1z68A3Ynh7bUkgcYk+EvH28c+4GslOZVLjxkVFjL99+8GW1lVdRbtJWFno89SlIPzYWczY1OMfXQ0BCtwCArkWu5EQqO9qZWZ71ceZaMV2b/jXtC5UEdDxVyIwvRjD3sR0GUhmnA4oglKQ5AYN1IUemWlrQyhx230UaKrWNrnqxE5iFd12XGDUf0++8owAFGb81A3BDAEEVuC7s1TN0QuIG5IXQ0zB1njpQ5GuZoGNhhI5XMSjH2prxUYEFZTRtA7zBXel8Ke5924ag9eQs6KXkPxBSDmziTwzrGb81fBH/MbAxPlSQ9qbpZP1PoUSR9usjgVYrSTmbwmJpB+AU1owtCnd5P0ZOEPZkgyv5n/x5IpJfUPJfo5q8TGLH/i4qjYRcqozY6kJob2tZ7tFgqEy80RWFq3J6gEGIjisHLQ0RSGOIAQTQgEiIWwpQkKDJjjGgMGwxRlCBDRyiywREm8A+LLbMIhcDMrMYQk4iAIIZCioiNKYYgkpCNS4jRgAJFGKIQDhnxJDAsaIRYBDOaIAZ3NCEZEyCkcBDmID5AlCBqDpMYBRGKDD/CTKhHibk6sAxQhFFEDEOIaohoF81AnyBqtIlac8lqtdYnJsqXRfeo69UBC6CGfHTMei4/nSTFN6OSZ6KEOnFrkERow0sTEVbQtK406kAM3Nqs4au5zNWt0BpOKfQr3/AbrsXue6BWnWxLm9eV+tzU+rou18tKIZTXJT7cuS5J7zk43BomtLfB+hthbyPqPcePyq1hB62VAPl1ozpyXhQfDMUxNYAlP1Xl/qoRfLGq5akao6EtOSOxzktZSF79DM5qpBi7oEMFMumqq0AUJ91F6qa43SvwYLT7t2hqEwyhD55//MG5fbtFY59EvR/UGJVzE3yU+vTkB4e+sNWKFpsDQnwnjsrOGhPZvckHdVWXxyWr/zVf6XVjmweQ1BitJtWsFNZHbLqFypwvsnp365yDOl53+xXMsLtBNrN2R5AbgjAEgnbM3GhpzNUOVNjSYEuBO2+TxWGfpIGlsGPmRksF7uuu1qpKOjUJ7sRIZTMa9tq46bKVcX5T6NeV1DfdRMt80apK3IEf1stMHFzolCf5WjxHwzMfGy1EU4mydWkAc12vlYvQnrcXIpdLmLqN1iTcwPUTXMCtFmLWiO7ipW3MnMHsLu5764Nly+r7pl5+qDZ34AtnFxgNu1uOVN7IlfE5lEEZWIijVxVScagiRf+ciUFQPTfVAsyjjWnu5uDTSnF9D3G61vMaYF/6Mx84QIoBO5pALMUS+i6krbNZfz0Y/aNt6Ix1UZ39ClnuUAjd/hE+2H7U8ayL8nI156bpa01Q8r1oToxi+X2si3NTARJWHwj5lWFgsF4J4dzE3RgeVsDQRtdJ0gLrK7SzYiHV7+0DVOB719C7jtZoa2LuJE+71TPgwJucoaypl0teFaiylftaNnkpvGMp4dhYDnFy4FivdbexcMxaFg/sDyjK/GDfxavtj59s/U/TqRLaGGzAAmsvegmbY5LQUL8W0KQrm8l0m7Psw79kUQjbu7gkKmei2oAaUD7g5Qe3r1Z77G6H7ruVHZhuYJf2pF26Jz3cwCsauUOTjn7SUU2g7g0SP01ZAhPa8p0wxw7cYBK6R9be6LfKKaFcLjGlXE4BgYuIf6g0ZBrQ4wz0hQN9N4Fc9gD4idu8uoz/afxNXoS/6TNnbsjc8HwXCJwLxJdc4Bhig8BPaRpDuQwIS+C9KQ67iPsqAXfJRld/lo1iqyIhTzMR9XHYt1BiTw++loVOHfSztdC5c5575PVzXPH6RWYmgetU7PjickC/ZjkYEJ8kSUIDhhOM05hgB0Xgx1EckyBJCYlTgk0SfCEwIA46PnNRu3Z7Gawf+f4MqmuXKiYPEOOXEWuAU4cH/x949Wzz+tpxwe8fM+veohCHOAUACGUxjkkUW3MnPqERpXEClCkmLHxFtTnL7XK5KmUu9cGqpfGSQy4HuB42gwshVqYL/1TdNbxS5jufo+k1mc+F9eoBrNnTYc3+2rAyP2BJGIVxkBr4aGpBhYrMooQBrmHMKInY3xbUWzEz62fATr4EbH4ZWNVy68DL/yLgus5r7IXQSKUM3pxZkEYYcLVoHhn//fCzr92Po2eiM3gMxP/8cRlF+0J3wAio7ddqXq5b8xI/BLePgjBNaJQEQRQ5ES9r6wl+CDR5HtAvwY03ea/2de9nZVlvfxTTUuysYR+8yvY6uN2qATmmJrZK3omdhmING2PvH7+ta/3PK7EV8IKAbqVA6PO6Wmj07e23aAlv3QUo9pGvle8oLfdTFDSw8055/5nBJNUNvxO/nPpl+wlQiUZOj5/L7Ccf7HUR0TJQmjfa9nHIdi3UhxDs/Ygro9Sn6ckv7HctfQSG/Q8E9jtc+7+U3v8XUEsHCIzaIDDOBwAA7xoAAFBLAQIUABQACAAIAE9Hj0DWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAT0ePQIzaIDDOBwAA7xoAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAABlCAAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | <ggb_applet width="303" height="336" version="4.0" ggbBase64="UEsDBBQACAAIAE9Hj0AAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAE9Hj0AAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1VnbjuM2En2efAUhBPs0lkmRus3aE7gbCHaAnswg3QmCfaMk2mYsS45I3xr5qfzIftMWScmW3T3evgw2iZEeimSxilWnblJG3+2WJdqIRsm6GnvExx4SVV4XspqNvbWeDhLvu/ffjGainoms4WhaN0uuxx4zlLIYe0GWh3QapwMRJtMBK7JwkKUZHRQRw0HGw1AUuYfQTsl3Vf0DXwq14rm4zediyW/qnGsreK716t1wuN1u/U6UXzez4WyW+TtVeAiuWamx1z68A3Ynh7bUkgcYk+EvH28c+4GslOZVLjxkVFjL99+8GW1lVdRbtJWFno89SlIPzYWczY1OMfXQ0BCtwCArkWu5EQqO9qZWZ71ceZaMV2b/jXtC5UEdDxVyIwvRjD3sR0GUhmnA4oglKQ5AYN1IUemWlrQyhx230UaKrWNrnqxE5iFd12XGDUf0++8owAFGb81A3BDAEEVuC7s1TN0QuIG5IXQ0zB1njpQ5GuZoGNhhI5XMSjH2prxUYEFZTRtA7zBXel8Ke5924ag9eQs6KXkPxBSDmziTwzrGb81fBH/MbAxPlSQ9qbpZP1PoUSR9usjgVYrSTmbwmJpB+AU1owtCnd5P0ZOEPZkgyv5n/x5IpJfUPJfo5q8TGLH/i4qjYRcqozY6kJob2tZ7tFgqEy80RWFq3J6gEGIjisHLQ0RSGOIAQTQgEiIWwpQkKDJjjGgMGwxRlCBDRyiywREm8A+LLbMIhcDMrMYQk4iAIIZCioiNKYYgkpCNS4jRgAJFGKIQDhnxJDAsaIRYBDOaIAZ3NCEZEyCkcBDmID5AlCBqDpMYBRGKDD/CTKhHibk6sAxQhFFEDEOIaohoF81AnyBqtIlac8lqtdYnJsqXRfeo69UBC6CGfHTMei4/nSTFN6OSZ6KEOnFrkERow0sTEVbQtK406kAM3Nqs4au5zNWt0BpOKfQr3/AbrsXue6BWnWxLm9eV+tzU+rou18tKIZTXJT7cuS5J7zk43BomtLfB+hthbyPqPcePyq1hB62VAPl1ozpyXhQfDMUxNYAlP1Xl/qoRfLGq5akao6EtOSOxzktZSF79DM5qpBi7oEMFMumqq0AUJ91F6qa43SvwYLT7t2hqEwyhD55//MG5fbtFY59EvR/UGJVzE3yU+vTkB4e+sNWKFpsDQnwnjsrOGhPZvckHdVWXxyWr/zVf6XVjmweQ1BitJtWsFNZHbLqFypwvsnp365yDOl53+xXMsLtBNrN2R5AbgjAEgnbM3GhpzNUOVNjSYEuBO2+TxWGfpIGlsGPmRksF7uuu1qpKOjUJ7sRIZTMa9tq46bKVcX5T6NeV1DfdRMt80apK3IEf1stMHFzolCf5WjxHwzMfGy1EU4mydWkAc12vlYvQnrcXIpdLmLqN1iTcwPUTXMCtFmLWiO7ipW3MnMHsLu5764Nly+r7pl5+qDZ34AtnFxgNu1uOVN7IlfE5lEEZWIijVxVScagiRf+ciUFQPTfVAsyjjWnu5uDTSnF9D3G61vMaYF/6Mx84QIoBO5pALMUS+i6krbNZfz0Y/aNt6Ix1UZ39ClnuUAjd/hE+2H7U8ayL8nI156bpa01Q8r1oToxi+X2si3NTARJWHwj5lWFgsF4J4dzE3RgeVsDQRtdJ0gLrK7SzYiHV7+0DVOB719C7jtZoa2LuJE+71TPgwJucoaypl0teFaiylftaNnkpvGMp4dhYDnFy4FivdbexcMxaFg/sDyjK/GDfxavtj59s/U/TqRLaGGzAAmsvegmbY5LQUL8W0KQrm8l0m7Psw79kUQjbu7gkKmei2oAaUD7g5Qe3r1Z77G6H7ruVHZhuYJf2pF26Jz3cwCsauUOTjn7SUU2g7g0SP01ZAhPa8p0wxw7cYBK6R9be6LfKKaFcLjGlXE4BgYuIf6g0ZBrQ4wz0hQN9N4Fc9gD4idu8uoz/afxNXoS/6TNnbsjc8HwXCJwLxJdc4Bhig8BPaRpDuQwIS+C9KQ67iPsqAXfJRld/lo1iqyIhTzMR9XHYt1BiTw++loVOHfSztdC5c5575PVzXPH6RWYmgetU7PjickC/ZjkYEJ8kSUIDhhOM05hgB0Xgx1EckyBJCYlTgk0SfCEwIA46PnNRu3Z7Gawf+f4MqmuXKiYPEOOXEWuAU4cH/x949Wzz+tpxwe8fM+veohCHOAUACGUxjkkUW3MnPqERpXEClCkmLHxFtTnL7XK5KmUu9cGqpfGSQy4HuB42gwshVqYL/1TdNbxS5jufo+k1mc+F9eoBrNnTYc3+2rAyP2BJGIVxkBr4aGpBhYrMooQBrmHMKInY3xbUWzEz62fATr4EbH4ZWNVy68DL/yLgus5r7IXQSKUM3pxZkEYYcLVoHhn//fCzr92Po2eiM3gMxP/8cRlF+0J3wAio7ddqXq5b8xI/BLePgjBNaJQEQRQ5ES9r6wl+CDR5HtAvwY03ea/2de9nZVlvfxTTUuysYR+8yvY6uN2qATmmJrZK3omdhmING2PvH7+ta/3PK7EV8IKAbqVA6PO6Wmj07e23aAlv3QUo9pGvle8oLfdTFDSw8055/5nBJNUNvxO/nPpl+wlQiUZOj5/L7Ccf7HUR0TJQmjfa9nHIdi3UhxDs/Ygro9Sn6ckv7HctfQSG/Q8E9jtc+7+U3v8XUEsHCIzaIDDOBwAA7xoAAFBLAQIUABQACAAIAE9Hj0DWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAT0ePQIzaIDDOBwAA7xoAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAABlCAAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| Zeile 32: | Zeile 34: | ||
|} | |} | ||
| − | ===Peripheriewinkel=== | + | ====Kreis==== |
| − | Unter einem Peripheriewinkel <math>\alpha</math> eines Kreises <math>k</math> versteht man einen Winkel, für den gilt: | + | {{Definition|::Es seien <math>M</math> ein Punkt der Ebene <math>\varepsilon</math> und <math>r>0</math> eine reelle Zahl. Die Menge aller Punkte der Ebene <math>\varepsilon</math>, die zu <math>M</math> den Abstand <math>r</math> haben, heißt Kreis mit dem Mittelpunkt <math>M</math> und Radius <math>r</math>. |
| + | }} | ||
| + | |||
| + | ====Peripheriewinkel==== | ||
| + | {{Definition|:Unter einem Peripheriewinkel <math>\alpha</math> eines Kreises <math>k</math> versteht man einen Winkel, für den gilt: | ||
# Der Scheitelpunkt <math>S</math> von <math>\alpha</math> ist ein Punkt des Kreises <math>k</math>. | # Der Scheitelpunkt <math>S</math> von <math>\alpha</math> ist ein Punkt des Kreises <math>k</math>. | ||
# Die Schenkel von <math>\alpha</math> haben außer <math>S</math> jeweils genau einen weiteren Punkt mit <math>k</math> gemeinsam. | # Die Schenkel von <math>\alpha</math> haben außer <math>S</math> jeweils genau einen weiteren Punkt mit <math>k</math> gemeinsam. | ||
| + | }} | ||
| − | + | ====Durchmesser==== | |
| − | < | + | {{Definition|:: Es sei <math>k</math> ein Kreis mit dem Mittelpunkt <math>M</math>. Jede Sehne von <math>k</math>, die <math>M</math> enthält, ist ein Durchmesser von <math>k</math>.}} |
| − | + | ||
| − | + | ==Kann man alles definieren?== | |
| + | Eine grundlegende Idee bei der Formulierung einer Definitionen ist die Verwendung von Oberbegriffen: | ||
| + | |||
| + | {{Definition|::Ein Quadrat ist eine Raute mit einem rechten Winkel.}} | ||
| + | |||
| + | Diese Definition des Begriffs ''Quadrat'' ist natürlich nur sinnvoll, wenn zunächst der Oberbegriff der ''Raute'' definiert wurde. In der Definition des Begriffs ''Raute'' könnte man jetzt den Oberbegriff ''Drachen'' verwenden, für den Begriff ''Drachen'' wiederum den Begriff ''Viereck'', für diesen ''n_Eck'' ... . | ||
| + | <iframe src="http://www.ph-heidelberg.de/wp/gieding//FLASHZ/HDV_AndreaSpitz.swf" width="500" height="300" frameborder="2"></iframe> | ||
| + | <br /> | ||
| + | <sub>(Obige Flash-Applikation wurde von Frau Andrea Spitz im Rahmen des Seminars "Erstellen von Multimediaanwendungen für den Unterricht" generiert.)</sub> | ||
| + | <br /> | ||
| + | Schließlich und letzten Endes landet man beim Begriff der ''Punktmenge''. Für diesen müsste klar definiert sein, was ein Punkt ist. Wir werden feststellen, dass wir im Rahmen der Art und Weise, wie wir hier Geometrie betreiben, nicht klar definieren können, was ein ''Punkt'' ist. | ||
| + | |||
| + | ''Punkte'', wie auch ''Geraden'' und ''Ebenen'' werden undefinierte Grundbegriffe sein. | ||
==Was ist eine Definition?== | ==Was ist eine Definition?== | ||
| Zeile 47: | Zeile 66: | ||
*Eine Definition ist nicht beweisbar und damit auch nicht wahr oder falsch sondern höchstens sinnvoll oder nicht sinnvoll.<br /> '''Anmerkung:''' Sie können z. B. eine Raute auf verschiedene Arten definieren. Alle Definitionen sollten aber immer die uns bekannte Raute beschreiben und nicht plötzlich eine andere Figur (Fünfeck, Trapez etc.). Das wäre dann natürlich schon falsch! Beispiele für in diesem Sinne falsche Definitionen finden Sie in den Übungen 1. | *Eine Definition ist nicht beweisbar und damit auch nicht wahr oder falsch sondern höchstens sinnvoll oder nicht sinnvoll.<br /> '''Anmerkung:''' Sie können z. B. eine Raute auf verschiedene Arten definieren. Alle Definitionen sollten aber immer die uns bekannte Raute beschreiben und nicht plötzlich eine andere Figur (Fünfeck, Trapez etc.). Das wäre dann natürlich schon falsch! Beispiele für in diesem Sinne falsche Definitionen finden Sie in den Übungen 1. | ||
*Eine Definition sollte so wenig wie möglich und so viel wie nötig beinhalten.<br />'''Anmerkung:''' Dabei schwingt immer eine gewisse Unschärfe mit, die sich didaktisch begründen lässt:<br /> Bsp. Definition Rechteck: <br />Ein Rechteck ist ein Viereck mit drei rechten Innenwinkel. <br />Diese Definition ist so knapp wie möglich gehalten. Insbesondere genügt es die Eigenschaft: "besitzt drei rechte Innenwinkel" zu beschreiben, da sich der vierte rechte Innenwinkel zwangsläufig ergibt. In der Regel wird man hier aber ein Rechteck als Viereck mit vier rechten Innenwinkel definieren, da diese Definition insbesondere für Schülerinnen und Schüler einsichtiger und griffiger ist.<br /><br /> | *Eine Definition sollte so wenig wie möglich und so viel wie nötig beinhalten.<br />'''Anmerkung:''' Dabei schwingt immer eine gewisse Unschärfe mit, die sich didaktisch begründen lässt:<br /> Bsp. Definition Rechteck: <br />Ein Rechteck ist ein Viereck mit drei rechten Innenwinkel. <br />Diese Definition ist so knapp wie möglich gehalten. Insbesondere genügt es die Eigenschaft: "besitzt drei rechte Innenwinkel" zu beschreiben, da sich der vierte rechte Innenwinkel zwangsläufig ergibt. In der Regel wird man hier aber ein Rechteck als Viereck mit vier rechten Innenwinkel definieren, da diese Definition insbesondere für Schülerinnen und Schüler einsichtiger und griffiger ist.<br /><br /> | ||
| + | |||
==Genau dasselbe, nur ganz anders: Arten, Definitionen zu formulieren== | ==Genau dasselbe, nur ganz anders: Arten, Definitionen zu formulieren== | ||
Es gibt verschiedene Arten, Definitionen zu formulieren. | Es gibt verschiedene Arten, Definitionen zu formulieren. | ||
| Zeile 99: | Zeile 119: | ||
<br /><br /> | <br /><br /> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | |} | ||
</div> | </div> | ||
Aktuelle Version vom 16. April 2012, 11:29 Uhr
VorbemerkungWenn im folgenden von Definitionen die Rede ist, dann im im Sinne einer mathematischen Definition. Beispiele für DefinitionenBegriffe, die im Satz des Thales verwendet werdenDer Satz des Thales
KreisDefinition
PeripheriewinkelDefinition
DurchmesserDefinition
Kann man alles definieren?Eine grundlegende Idee bei der Formulierung einer Definitionen ist die Verwendung von Oberbegriffen: Definition
Diese Definition des Begriffs Quadrat ist natürlich nur sinnvoll, wenn zunächst der Oberbegriff der Raute definiert wurde. In der Definition des Begriffs Raute könnte man jetzt den Oberbegriff Drachen verwenden, für den Begriff Drachen wiederum den Begriff Viereck, für diesen n_Eck ... .
[ www.ph-heidelberg.de is not an authorized iframe site ]
Punkte, wie auch Geraden und Ebenen werden undefinierte Grundbegriffe sein. Was ist eine Definition?
Genau dasselbe, nur ganz anders: Arten, Definitionen zu formulierenEs gibt verschiedene Arten, Definitionen zu formulieren. Beispiel 1: ggT zweier ganzer ZahlenDie Begriffe Teiler und Euklidischer Algorithmus seien im Folgenden bereits exakt definiert. Das Übliche, die Realdefinition
Konventionaldefinition, das Ganze in "wenn-dann"
Schön, aber wie bekomme ich den ggT: die genetisch, operative Definition
Beispiel 2: DrachenviereckDie Begriffe Dreieck, Viereck, Diagonale, Eckpunkt, Geradenspiegelung und achsensymmetrisch seien im Folgenden bereits definiert. Realdefinition
Konventionaldefinition
genetisch, operative Definition
Ein wenig Didaktik: Definitionen auf verschiedenen NiveaustufenAus didaktischer Sicht lassen sich Definitionen auf verschiedenen Niveaustufen formulieren.
Entwicklung einer "neuen" DefinitionIm Folgenden wollen wir versuchen, den (ihnen vermutlich wenig geläufigen) Begriff Ellipse zu definieren. Konstruktiv lässt sich eine Ellipse mit Hilfe der sogenannten Gärtnerkonstruktion, wie im folgenden Video, erzeugen. EmbedVideo erhielt die unbrauchbare ID „PQjeTmY0cdQ&NR=1“ für „youtube“.
Bemerkung zu obigem Video: Das geht natürlich noch schöner. Ansporn für Sie?
Aufgaben:
Vereinbarung: Wir setzen ebene Geometrie voraus. Definition E.1: EllipseDefinition K.1: Kreis als spezielle Ellipse
|
 über einem Durchmesser von
über einem Durchmesser von  ein Punkt der Ebene
ein Punkt der Ebene  und
und 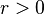 eine reelle Zahl. Die Menge aller Punkte der Ebene
eine reelle Zahl. Die Menge aller Punkte der Ebene  haben, heißt Kreis mit dem Mittelpunkt
haben, heißt Kreis mit dem Mittelpunkt  eines Kreises
eines Kreises  von
von  und
und  zwei ganze Zahlen.
zwei ganze Zahlen. 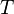 sei die Menge aller Zahlen, die sowohl Teiler von
sei die Menge aller Zahlen, die sowohl Teiler von  sowohl die ganze Zahl
sowohl die ganze Zahl  gibt, die auch
gibt, die auch  ein Dreieck und
ein Dreieck und 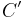 das Bild von
das Bild von  bei der Spiegelung an
bei der Spiegelung an  . Das Viereck
. Das Viereck 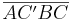 ist ein Drachenviereck.
ist ein Drachenviereck.

