Benutzer:Schnirch: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 4: | Zeile 4: | ||
Da die Schnittfläche <math>f(x)</math> an der Stelle x durch eine zentrische Streckung der Grundfläche ''A'' mit dem Faktor <math>\frac{x}{h}</math> entsteht, ist also <math>f(x) =\left( \frac{x}{h}\right) ^{2}\cdot A</math> und damit:<br /><math>V=\frac{A}{h^{2}}\int_{0}^{h} x^{2}\,dx= \frac{A}{h^{2}}\cdot\frac{1}{3}h^{3}=\frac{1}{3}A\cdot h </math>. (Keine Angst, dies ist kein Bestandteil der Veranstaltung sondern einfach nur eine gute Übung mit dem Formeleditor--[[Benutzer:Schnirch|Schnirch]] 12:13, 10. Okt. 2011 (CEST)) | Da die Schnittfläche <math>f(x)</math> an der Stelle x durch eine zentrische Streckung der Grundfläche ''A'' mit dem Faktor <math>\frac{x}{h}</math> entsteht, ist also <math>f(x) =\left( \frac{x}{h}\right) ^{2}\cdot A</math> und damit:<br /><math>V=\frac{A}{h^{2}}\int_{0}^{h} x^{2}\,dx= \frac{A}{h^{2}}\cdot\frac{1}{3}h^{3}=\frac{1}{3}A\cdot h </math>. (Keine Angst, dies ist kein Bestandteil der Veranstaltung sondern einfach nur eine gute Übung mit dem Formeleditor--[[Benutzer:Schnirch|Schnirch]] 12:13, 10. Okt. 2011 (CEST)) | ||
| − | [[ | + | [[Datei:Stifter_29.06.11-0005.jpg|200px]] |
Version vom 18. April 2012, 11:34 Uhr
Die Kukulkan-Pyramide in Chichén Itzá (Mexiko). Erbaut von den Mayas. Wer so was bauen kann, muss sich in Geometrie auskennen!
Volumen V einer Pyramide der Höhe h und der Schnittfläche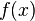 
einer Ebene F, die parallel zur Grundfläche A der Pyramide im Abstand x zur Spitze der Pyramide steht: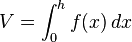 
Da die Schnittfläche 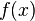an der Stelle x durch eine zentrische Streckung der Grundfläche A mit dem Faktor 
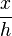entsteht, ist also 
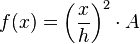und damit:
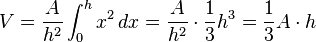. (Keine Angst, dies ist kein Bestandteil der Veranstaltung sondern einfach nur eine gute Übung mit dem Formeleditor--Schnirch 12:13, 10. Okt. 2011 (CEST))
