Zusatzaufgaben 2 (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| (10 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | == Aufgabe 1 == | |
| − | + | ||
Wir gehen von folgender Implikation aus: Wenn zwei Winkel Nebenwinkel sind, so sind sie supplementär.<br /> | Wir gehen von folgender Implikation aus: Wenn zwei Winkel Nebenwinkel sind, so sind sie supplementär.<br /> | ||
a) Wie lautet die Kontraposition dieser Implikation?<br /> | a) Wie lautet die Kontraposition dieser Implikation?<br /> | ||
b) Wie lautet die Annahme, wenn Sie diese Implikation durch einen Widerspruch beweisen möchten?<br /> | b) Wie lautet die Annahme, wenn Sie diese Implikation durch einen Widerspruch beweisen möchten?<br /> | ||
| + | |||
[[Lösung von Zusatzaufgabe 2.1 (SoSe_12)]] | [[Lösung von Zusatzaufgabe 2.1 (SoSe_12)]] | ||
| − | + | == Aufgabe 2 == | |
| − | Beweisen Sie | + | Beweisen Sie mit Hilfe einer Wahrheitstabelle:<br /><br /> |
| − | + | <math>(\ A \Rightarrow B) \ \Leftrightarrow (\neg B \Rightarrow \neg A)</math><br /> | |
| − | + | Inwiefern hilft Ihnen diese Äquvalenz, wenn Sie einen geometrischen Satz beweisen wollen?<br /> | |
| − | + | ||
| − | + | ||
[[Lösung von Zusatzaufgabe 2.2 (SoSe_12)]] | [[Lösung von Zusatzaufgabe 2.2 (SoSe_12)]] | ||
| − | + | == Aufgabe 3 == | |
Beweisen Sie die Äquvalenzaussage | Beweisen Sie die Äquvalenzaussage | ||
| − | '''Für alle n <math>\epsilon</math> <math>\mathbb{N}</math> gilt: n ist gerade <math>\Leftrightarrow</math> n<sup>2</sup> ist gerade.''' | + | '''Für alle n <math>\epsilon</math> <math>\mathbb{N}</math> gilt: n ist gerade <math>\Leftrightarrow</math> n<sup>2</sup> ist gerade.'''<br /> |
| + | |||
[[Lösung von Zusatzaufgabe 2.3 (SoSe_12)]] | [[Lösung von Zusatzaufgabe 2.3 (SoSe_12)]] | ||
Aktuelle Version vom 19. April 2012, 09:46 Uhr
Aufgabe 1
Wir gehen von folgender Implikation aus: Wenn zwei Winkel Nebenwinkel sind, so sind sie supplementär.
a) Wie lautet die Kontraposition dieser Implikation?
b) Wie lautet die Annahme, wenn Sie diese Implikation durch einen Widerspruch beweisen möchten?
Lösung von Zusatzaufgabe 2.1 (SoSe_12)
Aufgabe 2
Beweisen Sie mit Hilfe einer Wahrheitstabelle:
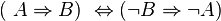
Inwiefern hilft Ihnen diese Äquvalenz, wenn Sie einen geometrischen Satz beweisen wollen?
Lösung von Zusatzaufgabe 2.2 (SoSe_12)
Aufgabe 3
Beweisen Sie die Äquvalenzaussage
Für alle n 
 gilt: n ist gerade
gilt: n ist gerade  n2 ist gerade.
n2 ist gerade.

