Definieren des Begriffs Nebenwinkel: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Warum Gemecker beim Begriff benachbarte Winkeln?) |
*m.g.* (Diskussion | Beiträge) (→Folien aus der Übung hier einbinden:) |
||
| Zeile 18: | Zeile 18: | ||
Hier wurde Beispiel 1 als Kausaldefinition formuliert. Zusätzlich wurde die Eigenschaft "benachbart" verwendet. Die definierende Eigenschaft ist also: "supplementär und benachbart". Diese ist notwendig und hinreichend dafür, dass zwei Winkel Nebenwinkel sind. Das Problem besteht allerdings darin, dass nicht so recht geklärt ist, was benachbarte Winkel sind. Damit kann die Definition nur als informelle Definition und nicht als formal korrekte Definition gewertet werden. Für den Unterricht in der SI wäre das in Ordnung aus formal mathematischer Sicht ist nachzubessern: Was heißt zwei Winkel sind benachbart? --[[Benutzer:*m.g.*|*m.g.*]] 19:09, 21. Apr. 2012 (CEST) | Hier wurde Beispiel 1 als Kausaldefinition formuliert. Zusätzlich wurde die Eigenschaft "benachbart" verwendet. Die definierende Eigenschaft ist also: "supplementär und benachbart". Diese ist notwendig und hinreichend dafür, dass zwei Winkel Nebenwinkel sind. Das Problem besteht allerdings darin, dass nicht so recht geklärt ist, was benachbarte Winkel sind. Damit kann die Definition nur als informelle Definition und nicht als formal korrekte Definition gewertet werden. Für den Unterricht in der SI wäre das in Ordnung aus formal mathematischer Sicht ist nachzubessern: Was heißt zwei Winkel sind benachbart? --[[Benutzer:*m.g.*|*m.g.*]] 19:09, 21. Apr. 2012 (CEST) | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Beispiel 3=== | ===Beispiel 3=== | ||
Version vom 22. April 2012, 17:02 Uhr
|
Übung mit dem Classroompresenter vom 20. April 2012
Alle Deck'sHTML-Dokument mit allen Folien der Übung zum Durchblättern Definieren des Begriffs NebenwinkelVariante 1: Mit Verwendung des Begriffs supplementärBeispiel 1: Es wurde nur eine hinreichende Bedingung für die Definition verwendet[ www.ph-heidelberg.de is not an authorized iframe site ] Als Kausaldefinition würde obige Definition lauten: Wenn zwei Winkel sich zu Beispiel 2: Kausaldefinition, fast wie Beispiel 1[ www.ph-heidelberg.de is not an authorized iframe site ] Hier wurde Beispiel 1 als Kausaldefinition formuliert. Zusätzlich wurde die Eigenschaft "benachbart" verwendet. Die definierende Eigenschaft ist also: "supplementär und benachbart". Diese ist notwendig und hinreichend dafür, dass zwei Winkel Nebenwinkel sind. Das Problem besteht allerdings darin, dass nicht so recht geklärt ist, was benachbarte Winkel sind. Damit kann die Definition nur als informelle Definition und nicht als formal korrekte Definition gewertet werden. Für den Unterricht in der SI wäre das in Ordnung aus formal mathematischer Sicht ist nachzubessern: Was heißt zwei Winkel sind benachbart? --*m.g.* 19:09, 21. Apr. 2012 (CEST) Beispiel 3[ www.ph-heidelberg.de is not an authorized iframe site ] Wie Beispiel 2, nur nicht in Wenn-Dann. Auch hier wissen wir nicht wirklich, was es heißt, zwei Winkel sind benachbart. Ggf. würde der Mathematiker auch bemängeln, dass es genauer heißen müsste: ...deren Größen zusammen 180° ergeben... . Warum Gemecker beim Begriff benachbarte Winkeln?
|
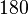° ergänzen, so sind sie Nebenwinkel. Da es auch Winkel gibt, die zwar supplementär, aber keine Nebenwinkel sind, ist die obige Formulierung keine korrekte Definition des Begriffs Nebenwinkel. Die definierende Eigenschaft muss immer hinreichend und notwendig sein.--
und 
von benachbarten Winkel. Definiert ist das meist nirgends. Würden Sie definieren was es bedeutet, zwei Winkel sind benachbart, wären Sie aus dem Schneider. Wie würde eine solche Definition aussehen?
