Definieren des Begriffs Nebenwinkel: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Beispiel 3: Wie Beispiel 2, nur nicht konventional) |
*m.g.* (Diskussion | Beiträge) (→Korrekte Definitionen) |
||
| (8 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
Folie im oben verlinkten html-Dokument auswählen. Rechte Maustaste drauf, Bild in neuem Tab öffnen. Dort die Adresse des Bildes auf meiner PH-Seite kopieren, Mittels iframe hier einbinden. Wie das funktioniert sehen sie im Quelltext der vorangegangenen Beispiele. --[[Benutzer:*m.g.*|*m.g.*]] 19:34, 21. Apr. 2012 (CEST) | Folie im oben verlinkten html-Dokument auswählen. Rechte Maustaste drauf, Bild in neuem Tab öffnen. Dort die Adresse des Bildes auf meiner PH-Seite kopieren, Mittels iframe hier einbinden. Wie das funktioniert sehen sie im Quelltext der vorangegangenen Beispiele. --[[Benutzer:*m.g.*|*m.g.*]] 19:34, 21. Apr. 2012 (CEST) | ||
| − | Es reicht auch aus, wenn Sie den Quelltext <pre><iframe src="http://www.ph-heidelberg.de/wp/gieding/uebungen/20_04_12/Student Submissions_files/Student Submissions_043.png" width="720" height="540" frameborder="2"></iframe></pre> | + | Es reicht auch aus, wenn Sie den Quelltext<br /> <pre><iframe src="http://www.ph-heidelberg.de/wp/gieding/uebungen/20_04_12/Student Submissions_files/Student Submissions_043.png" width="720" height="540" frameborder="2"></iframe></pre> |
einfügen und nur die Nummer der Folie ändern (Student Submissions_043.png etwa in Student Submissions_045.png ändern) Viel Erfolg! | einfügen und nur die Nummer der Folie ändern (Student Submissions_043.png etwa in Student Submissions_045.png ändern) Viel Erfolg! | ||
| Zeile 29: | Zeile 29: | ||
Wie Beispiel 2, nur nicht in ''Wenn-Dann''. Auch hier wissen wir nicht wirklich, was es heißt, zwei Winkel sind benachbart. Ggf. würde der Mathematiker auch bemängeln, dass es genauer heißen müsste: ''...deren Größen zusammen 180° ergeben... . | Wie Beispiel 2, nur nicht in ''Wenn-Dann''. Auch hier wissen wir nicht wirklich, was es heißt, zwei Winkel sind benachbart. Ggf. würde der Mathematiker auch bemängeln, dass es genauer heißen müsste: ''...deren Größen zusammen 180° ergeben... . | ||
'' | '' | ||
| − | |||
| − | |||
| − | |||
===Warum Gemecker beim Begriff benachbarte Winkeln?=== | ===Warum Gemecker beim Begriff benachbarte Winkeln?=== | ||
[[Datei: Parallelogramm 05.png| 300px]]<br /><br /> | [[Datei: Parallelogramm 05.png| 300px]]<br /><br /> | ||
In der Regel spricht man bei <math>\alpha</math> und <math>\beta</math> von benachbarten Winkel. Definiert ist das meist nirgends. Würden Sie definieren was es bedeutet, zwei Winkel sind benachbart, wären Sie aus dem Schneider. Wie würde eine solche Definition aussehen? | In der Regel spricht man bei <math>\alpha</math> und <math>\beta</math> von benachbarten Winkel. Definiert ist das meist nirgends. Würden Sie definieren was es bedeutet, zwei Winkel sind benachbart, wären Sie aus dem Schneider. Wie würde eine solche Definition aussehen? | ||
| + | ==Variante 2: Idee der Supplementwinkel darf nicht verwendet werden== | ||
| + | ===Beispiel 4=== | ||
| + | <iframe src="http://www.ph-heidelberg.de/wp/gieding/uebungen/20_04_12/Student Submissions_files/Student Submissions_059.png" width="720" height="540" frameborder="2"></iframe> | ||
| + | |||
| + | #gemeinsamer Schenkel | ||
| + | #Gerade bilden | ||
| + | |||
| + | Das ist schon mal super. Nur die Formulierung macht mir Sorgen. Ein Winkel ist ein Paar von Halbgeraden, die den Anfangspunkt gemeinsam haben. Zwei Winkel sind also zwei Paare von Halbgerade, macht insgesamt 4 Halbgeraden. Abgesehen von Nullwinkeln werden die Halbgeraden nicht identisch sein. Wie sollen 4 Halbgeraden eine Gerade bilden? Und ist es das eigentlich was wir wollen? Sollen wirklich alle vier Schenkel (Halbgeraden) gemeinsam eine Gerade bilden?--[[Benutzer:*m.g.*|*m.g.*]] 18:15, 22. Apr. 2012 (CEST) | ||
| + | |||
| + | ==Korrekte Definitionen== | ||
| + | {{Definition|(Nebenwinkel)<br />Wenn zwei Winkel einen Schenkel gemeinsam haben und die Vereinigungsmenge der anderen beiden Schenkel dieser Winkel eine Gerade ist, dann bilden die beiden Winkel ein Paar von Nebenwinkeln.}}--[[Benutzer:*m.g.*|*m.g.*]] 18:35, 22. Apr. 2012 (CEST) | ||
| + | |||
| + | |||
| + | |||
<!--- Das, was hier drunter steht muss stehen bleiben, also oberhalb dieses Kommentars Änderungen einfügen ---> | <!--- Das, was hier drunter steht muss stehen bleiben, also oberhalb dieses Kommentars Änderungen einfügen ---> | ||
|} | |} | ||
Aktuelle Version vom 22. April 2012, 17:35 Uhr
|
Übung mit dem Classroompresenter vom 20. April 2012
Alle Deck'sHTML-Dokument mit allen Folien der Übung zum Durchblättern Folien aus der Übung hier einbinden:Folie im oben verlinkten html-Dokument auswählen. Rechte Maustaste drauf, Bild in neuem Tab öffnen. Dort die Adresse des Bildes auf meiner PH-Seite kopieren, Mittels iframe hier einbinden. Wie das funktioniert sehen sie im Quelltext der vorangegangenen Beispiele. --*m.g.* 19:34, 21. Apr. 2012 (CEST) Es reicht auch aus, wenn Sie den Quelltext<iframe src="http://www.ph-heidelberg.de/wp/gieding/uebungen/20_04_12/Student Submissions_files/Student Submissions_043.png" width="720" height="540" frameborder="2"></iframe> einfügen und nur die Nummer der Folie ändern (Student Submissions_043.png etwa in Student Submissions_045.png ändern) Viel Erfolg! Definieren des Begriffs NebenwinkelVariante 1: Mit Verwendung des Begriffs supplementärBeispiel 1: Es wurde nur eine hinreichende Bedingung für die Definition verwendet[ www.ph-heidelberg.de is not an authorized iframe site ] Als Kausaldefinition würde obige Definition lauten: Wenn zwei Winkel sich zu Beispiel 2: Kausaldefinition, fast wie Beispiel 1[ www.ph-heidelberg.de is not an authorized iframe site ] Hier wurde Beispiel 1 als Kausaldefinition formuliert. Zusätzlich wurde die Eigenschaft "benachbart" verwendet. Die definierende Eigenschaft ist also: "supplementär und benachbart". Diese ist notwendig und hinreichend dafür, dass zwei Winkel Nebenwinkel sind. Das Problem besteht allerdings darin, dass nicht so recht geklärt ist, was benachbarte Winkel sind. Damit kann die Definition nur als informelle Definition und nicht als formal korrekte Definition gewertet werden. Für den Unterricht in der SI wäre das in Ordnung aus formal mathematischer Sicht ist nachzubessern: Was heißt zwei Winkel sind benachbart? --*m.g.* 19:09, 21. Apr. 2012 (CEST) Beispiel 3: Wie Beispiel 2, nur nicht konventional formuliert[ www.ph-heidelberg.de is not an authorized iframe site ] Wie Beispiel 2, nur nicht in Wenn-Dann. Auch hier wissen wir nicht wirklich, was es heißt, zwei Winkel sind benachbart. Ggf. würde der Mathematiker auch bemängeln, dass es genauer heißen müsste: ...deren Größen zusammen 180° ergeben... . Warum Gemecker beim Begriff benachbarte Winkeln?
Variante 2: Idee der Supplementwinkel darf nicht verwendet werdenBeispiel 4[ www.ph-heidelberg.de is not an authorized iframe site ]
Das ist schon mal super. Nur die Formulierung macht mir Sorgen. Ein Winkel ist ein Paar von Halbgeraden, die den Anfangspunkt gemeinsam haben. Zwei Winkel sind also zwei Paare von Halbgerade, macht insgesamt 4 Halbgeraden. Abgesehen von Nullwinkeln werden die Halbgeraden nicht identisch sein. Wie sollen 4 Halbgeraden eine Gerade bilden? Und ist es das eigentlich was wir wollen? Sollen wirklich alle vier Schenkel (Halbgeraden) gemeinsam eine Gerade bilden?--*m.g.* 18:15, 22. Apr. 2012 (CEST) Korrekte DefinitionenDefinition (Nebenwinkel)
|
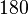° ergänzen, so sind sie Nebenwinkel. Da es auch Winkel gibt, die zwar supplementär, aber keine Nebenwinkel sind, ist die obige Formulierung keine korrekte Definition des Begriffs Nebenwinkel. Die definierende Eigenschaft muss immer hinreichend und notwendig sein.--
und 
von benachbarten Winkel. Definiert ist das meist nirgends. Würden Sie definieren was es bedeutet, zwei Winkel sind benachbart, wären Sie aus dem Schneider. Wie würde eine solche Definition aussehen?
