Lösung von Aufgabe 2.6 S (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „ ==Aufgabe 2.6== Das Parallelenaxiom lautet wie folgt:<br /> Zu jeder Geraden ''g'' und zu jedem nicht auf ''g'' liegenden Punkt ''A'' gibt es höchstens eine Ge…“) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 2.6) |
||
| Zeile 1: | Zeile 1: | ||
==Aufgabe 2.6== | ==Aufgabe 2.6== | ||
| − | + | ==Aufgabe 2.6== | |
| − | + | Bringen Sie die folgenden Implikationen in die Form ''Wenn-Dann'': | |
| − | + | # Jedes Quadrat hat vier rechte Innenwinkel. | |
| − | + | # Der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks liegt auf der Hypotenuse dieses Dreiecks. | |
| − | + | # In einem konvexen Viereck schneiden sich die Diagonalen des Vierecks. | |
| − | + | # Die Geraden, die durch die Diagonalen einer Raute <math>\overline{ABCD}</math>eindeutig bestimmt sind, sind Symmetrieachsen von <math>\overline{ABCD}</math>. | |
| + | # Es sei <math>\overline{PQRS}</math> ein Paralellogramm. Es gilt: <math>\angle SPQ \tilde= \angle QRS </math>. | ||
| + | # Die Innenwinkelsumme im Dreieck beträgt 180°. | ||
[[Category:Einführung_S]] | [[Category:Einführung_S]] | ||
Version vom 26. April 2012, 10:00 Uhr
Aufgabe 2.6
Aufgabe 2.6
Bringen Sie die folgenden Implikationen in die Form Wenn-Dann:
- Jedes Quadrat hat vier rechte Innenwinkel.
- Der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks liegt auf der Hypotenuse dieses Dreiecks.
- In einem konvexen Viereck schneiden sich die Diagonalen des Vierecks.
- Die Geraden, die durch die Diagonalen einer Raute
 eindeutig bestimmt sind, sind Symmetrieachsen von
eindeutig bestimmt sind, sind Symmetrieachsen von  .
.
- Es sei
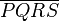 ein Paralellogramm. Es gilt:
ein Paralellogramm. Es gilt: 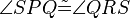 .
.
- Die Innenwinkelsumme im Dreieck beträgt 180°.

