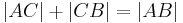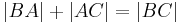Strecken und Halbgeraden SoSe 12: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „= Strecken, intuitiv = Punkte, Geraden und auch Ebenen sind Grundbegriffe, die wir in unserer Geometrie nicht definieren können. Für Strecken wird uns das gelin…“) |
|||
| Zeile 48: | Zeile 48: | ||
::Aus <math> \operatorname{Zw} \left( A, B, C \right) </math> folgt <math> \operatorname{Zw} \left( C, B, A \right) </math>. | ::Aus <math> \operatorname{Zw} \left( A, B, C \right) </math> folgt <math> \operatorname{Zw} \left( C, B, A \right) </math>. | ||
| − | ===== Beweis von Satz | + | ===== Beweis von Satz I.1 ===== |
:: Beweis: trivial (Der Leser überzeuge sich davon.) | :: Beweis: trivial (Der Leser überzeuge sich davon.) | ||
| Zeile 55: | Zeile 55: | ||
::Aus <math> \operatorname{Zw} \left( A, B, C \right) </math> folgt <math> \operatorname{koll} \left( A, B, C \right) </math>. | ::Aus <math> \operatorname{Zw} \left( A, B, C \right) </math> folgt <math> \operatorname{koll} \left( A, B, C \right) </math>. | ||
| − | ===== Beweis von Satz | + | ===== Beweis von Satz I.2 ===== |
:: Beweis: trivial (Der Leser überzeuge sich davon.) | :: Beweis: trivial (Der Leser überzeuge sich davon.) | ||
| Zeile 62: | Zeile 62: | ||
::Es sei <math> \operatorname{koll} \left( A, B, C \right) </math> mit <math>\ A, B, C</math> sind paarweise verschieden.<br /> Dann gilt <math> \operatorname{Zw} \left( A, B, C \right) </math> oder <math> \operatorname{Zw} \left( A, C, B \right) </math> oder <math> \operatorname{Zw} \left( B, A, C \right) </math>. | ::Es sei <math> \operatorname{koll} \left( A, B, C \right) </math> mit <math>\ A, B, C</math> sind paarweise verschieden.<br /> Dann gilt <math> \operatorname{Zw} \left( A, B, C \right) </math> oder <math> \operatorname{Zw} \left( A, C, B \right) </math> oder <math> \operatorname{Zw} \left( B, A, C \right) </math>. | ||
| − | ===== Beweis von Satz | + | ===== Beweis von Satz I.3: ===== |
::<span style="color: blue">Übungsaufgabe</span> | ::<span style="color: blue">Übungsaufgabe</span> | ||
| Zeile 82: | Zeile 82: | ||
Der Begriff des Abstands zweier Punkt ist ebenfalls ein Grundbegriff, den wir nicht definieren werden können. Mit dem Abstand können wir aber einer Strecke eindeutig eine Länge zuordnen. | Der Begriff des Abstands zweier Punkt ist ebenfalls ein Grundbegriff, den wir nicht definieren werden können. Mit dem Abstand können wir aber einer Strecke eindeutig eine Länge zuordnen. | ||
| − | ===== Definition | + | ===== Definition I.4: (Länge einer Strecke) ===== |
::Es seien <math>\ A</math> und <math>\ B</math> zwei verschiedene Punkte. ... (ergänzen Sie) | ::Es seien <math>\ A</math> und <math>\ B</math> zwei verschiedene Punkte. ... (ergänzen Sie) | ||
Version vom 14. Mai 2012, 13:46 Uhr
Inhaltsverzeichnis |
Strecken, intuitiv
Punkte, Geraden und auch Ebenen sind Grundbegriffe, die wir in unserer Geometrie nicht definieren können. Für Strecken wird uns das gelingen.
Eine intuitive Vorstellung von Strecken haben wir schon: Eine Strecke ist die kürzeste Verbindung zwischen zwei Punkten. Diese Vorstellung gilt es nun zu präzisieren.
Da wir alle unsere geometrischen Objekte als Punktmengen betrachten, wäre es schön, wenn wir die Strecke als Menge von Punkten mit bestimmten Eigenschaften definieren könnten. An dieser Stelle brauchen wir eine neue Relation, die so genannte Zwischenrelation, die uns diese benötigten Eigenschaften liefert:
Definition I/1: (kollinear)
- Eine Menge von Punkten heißt kollinear, wenn es eine Gerade gibt, die alle Punkte der Menge enthält.
- Schreibweise: koll(A, B, C, ...) Sollten die Punkte A, B, C einer Menge nicht kollinear sein, so schreibt man:nkoll(A, B, C)
Die Dreiecksungleichung
Schüler entdecken die Dreiecksungleichung
Dreieckskonstruktionen sind seit jeher fester Bestandteil des Geometrieunterrichts in der Schule. Neben solchen allgemeinen Zielen wie Erziehung zur Exaktheit und Sauberkeit bei Konstruktionen, geht es bei diesen Aufgaben auch darum, dass die Schüler die Gesetzmäßigkeiten ihrer Umwelt durch eigene Tätigkeit selbst erfahren.
Die einfachsten Dreieckskonstruktionen sind die, bei denen die Längen der drei Seiten eines Dreiecks gegeben sind.
Der Lehrer, der Konstruktionsaufgaben auf das eigentliche Generieren einer Zeichnung durch die Schüler reduziert, verschenkt eine Reihe von Potenzen hinsichtlich verschiedenster Ziele des Mathematikunterrichts. Stellvertretend sei in diesem Zusammenhang das Begründen genannt.
Aus didaktischer Sicht werden Konstruktionsaufgaben zu einem bestimmten Problemkreis erst dann vollständig, wenn die Schüler sich sowohl mit Aufgaben mit mehreren Lösungsmöglichkeiten als auch mit unlösbaren Aufgaben auseinandersetzen müssen.
Experimentieren Sie mit dem folgenden Geogebraapplet und klassifizireren Sie die Typen von Konstruktionsaufgaben, die sich für Dreieckskonstruktionen nach SSS ergeben:
Die Dreiecksungleichung
- Für drei beliebige Punkte
und 
gilt: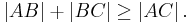 
- Für drei beliebige Punkte
- Falls
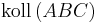, dann ist eine der folgenden Gleichungen erfüllt:
- Falls
- Ist umgekehrt eine dieser drei Gleichungen erfüllt, so sind
, 
und kollinear.
Definitionen und Sätze
Definition I.2: (Zwischenrelation)
- Ein Punkt liegt zwischen zwei Punkten und , wenn
gilt und der Punkt sowohl von als auch von verschieden ist.
- Ein Punkt
- Schreibweise:
- Schreibweise:
Unmittelbar einsichtig sind die folgenden beiden Sätze:
Satz I.1
- Aus folgt
.
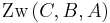- Aus
Beweis von Satz I.1
- Beweis: trivial (Der Leser überzeuge sich davon.)
Satz I.2:
- Aus folgt
.
- Aus
Beweis von Satz I.2
- Beweis: trivial (Der Leser überzeuge sich davon.)
Satz I.3
- Es sei mit
sind paarweise verschieden.
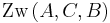Dann gilt oder 
oder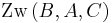 
.
- Es sei
Beweis von Satz I.3:
- Übungsaufgabe
Der Begriff der Strecke
Definition I.3: (Strecke, Endpunkte einer Strecke)
- Es seien und zwei verschiedene Punkte. ... (ergänzen Sie)
- Es seien
Längenmessung
Messen: Andere Länder andere Sitten
Rory, ein irischer Schüler, wechselt für ein Jahr an die IGH im Hasenleiser. Die Beibehaltung gewisser Gewohnheiten aus Irland könnte für Rory in Deutschland Probleme mit sich bringen: In Irland schmeckt das Guinness besser und vor allem wird es in der Maßeinheit Pint ausgeschenkt. Ein Pint ist etwas mehr als ein halber Liter: 0,56826125 l.
Rory ist ein sehr ordentlicher Schüler und hat sein Schullineal aus Irland mitgebracht. Zum Messen würde dieses in Deutschland allerdings nur dann etwas nützen, wenn es über eine zweite Skale in cm verfügen würde.
Die Idee der Längenmessung
Strecken werden bereits in Klasse 1 gemessen. Was ist das eigentlich, das Messen von Strecken. Wie würden Sie es den Schülern der Klassenstufen für die Sie ausgebildet werden erklären? Ergänzen Sie hier:
Der Abstand zweier Punkte
Der Begriff des Abstands zweier Punkt ist ebenfalls ein Grundbegriff, den wir nicht definieren werden können. Mit dem Abstand können wir aber einer Strecke eindeutig eine Länge zuordnen.
Definition I.4: (Länge einer Strecke)
- Es seien und zwei verschiedene Punkte. ... (ergänzen Sie)
- Es seien
Halbgeraden bzw. Strahlen
So ist es gemeint
Hinweis: Klicken Sie auf das Symbol rechts oben (neu laden), damit alles richtig angezeigt wird.
Manipulieren Sie dann erst P und dann B und A.
Definition I.5: (Halbgerade, bzw. Strahl)
- Definition: Halbgerade
(ergänzen Sie)
- Definition: Halbgerade
(ergänzen Sie)
Satz I.4
- Es sei
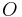ein Punkt einer Geraden 
.
Die Teilmengen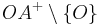
, 
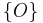und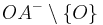 
bilden eine Klasseneinteilung der Geraden .
- Es sei
Beweis von Satz I.4
(ergänzen Sie)
