Lösung von Aufgabe 6.5P (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Gegeben seien drei paarweise verschiedene und '''kollineare''' Punkte ''A'', ''B'' und ''C'' in einer Ebene ''E''. Ferner sei eine Gerade ''g'' Teilmenge der Eben…“) |
|||
| Zeile 4: | Zeile 4: | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
| + | Im Enteffekt ist das doch nur wieder der Satz von Patsch ( seine Umkehrung ?) | ||
| + | Ist ja wieder das Ebenenteilungsaxiom!oder? | ||
| + | Denn wenn die Strecke AB g schneidet und die BC nicht geschnitten wird dann muss wegen des Satz von Patsch g die Streche AC schneiden! | ||
Version vom 1. Juni 2012, 12:53 Uhr
Gegeben seien drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E. Ferner sei eine Gerade g Teilmenge der Ebene E, wobei keiner der Punkte A, B und C auf g liegen möge. Beweisen Sie folgenden Zusammenhang:
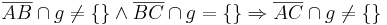
Im Enteffekt ist das doch nur wieder der Satz von Patsch ( seine Umkehrung ?)
Ist ja wieder das Ebenenteilungsaxiom!oder?
Denn wenn die Strecke AB g schneidet und die BC nicht geschnitten wird dann muss wegen des Satz von Patsch g die Streche AC schneiden!

