Lösung von Aufgabe 6.5P (SoSe 12): Unterschied zwischen den Versionen
| (2 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
Im Enteffekt ist das doch nur wieder der Satz von Patsch ( seine Umkehrung ?) | Im Enteffekt ist das doch nur wieder der Satz von Patsch ( seine Umkehrung ?) | ||
Ist ja wieder das Ebenenteilungsaxiom!oder? | Ist ja wieder das Ebenenteilungsaxiom!oder? | ||
| − | Denn wenn die Strecke AB g schneidet und die BC nicht geschnitten wird dann muss wegen des Satz von Patsch g die Streche AC schneiden!knechtk | + | Denn wenn die Strecke AB g schneidet und die BC nicht geschnitten wird dann muss wegen des Satz von Patsch g die Streche AC schneiden!knechtk<br /><br /> |
| + | |||
| + | die punkte sollen in diesem fall '''kollinear''' sein, also auf einer "linie" liegen. | ||
| + | * damit ist es nicht der Satz von Pasch, aber diesen könnte man sicher für den Beweis verwenden!--[[Benutzer:Tutorin Anne|Tutorin Anne]] 15:48, 6. Jun. 2012 (CEST) | ||
| + | ''' | ||
| + | Wer versucht's mal selber?''' z.B. Tabelarisch:--[[Benutzer:Tutorin Anne|Tutorin Anne]] 15:53, 6. Jun. 2012 (CEST)<br /> | ||
| + | {| class="wikitable" | ||
| + | | Voraussetzung || (V. hier eintragen) | ||
| + | |- | ||
| + | | Behauptung || (Beh. hier eintragen) | ||
| + | |} | ||
| + | <br /> | ||
| + | |||
| + | {| class="wikitable" | ||
| + | !Beweisschritt!!Begründung | ||
| + | |- | ||
| + | | 1 (Schritt 1)|| (Begründung 1) | ||
| + | |- | ||
| + | | 2 (Schritt 2) || (Begründung 2) | ||
| + | |- | ||
| + | | 3 (Schritt) || (Begründung) | ||
| + | |- | ||
| + | | 4 (Schritt) || (Begründung) | ||
| + | |} | ||
| + | <br /> | ||
| + | |||
| + | Hier unten kommt gleich eine Lösung von Studentin.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 15:53, 6. Jun. 2012 (CEST)<br /> | ||
| + | wir haben also eine ebene e, in der eine gerade g liegt. <br /> | ||
| + | außerdem liegt in der ebene e die punkte a, b, c, diese dürfen nicht auf der geraden g liegen.<br /><br /> | ||
| + | voraussetzung: <math>\overline{AB} \cap g \neq \lbrace \rbrace \wedge \overline{BC} \cap g = \lbrace \rbrace</math><br /> | ||
| + | behauptung: <math>\overline{AC} \cap g \neq \lbrace \rbrace </math><br /> | ||
| + | [[Datei:6.5.p.JPG|300px]]<br /> | ||
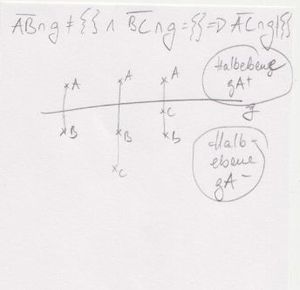
| + | ich nehme mir nur den punkt a, um die ebene in zwei halbebenen ga+ und ga- zu teilen.<br /> | ||
| + | laut voraussetzung schneidet die strecke ab die gerade g, daher muss b auf ga- liegen (laut unserer def. der halbebenen)<br /> | ||
| + | da die strecke bc die gerade g nicht schneidet (siehe voraussetzung), liegt c (wie ebenso b) auf der halbebenen ga-.<br /> | ||
| + | daher muss die strecke ac die gerade g schneiden: denn a liegt auf ga+ und c auf ga-<br /> | ||
| + | reicht das so?<br /> Ja, so kann man es beweisen!--[[Benutzer:Tutorin Anne|Tutorin Anne]] 15:53, 6. Jun. 2012 (CEST) | ||
| + | --[[Benutzer:Studentin|Studentin]] 16:35, 3. Jun. 2012 (CEST) | ||
Aktuelle Version vom 6. Juni 2012, 15:53 Uhr
Gegeben seien drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E. Ferner sei eine Gerade g Teilmenge der Ebene E, wobei keiner der Punkte A, B und C auf g liegen möge. Beweisen Sie folgenden Zusammenhang:
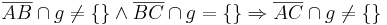
Im Enteffekt ist das doch nur wieder der Satz von Patsch ( seine Umkehrung ?)
Ist ja wieder das Ebenenteilungsaxiom!oder?
Denn wenn die Strecke AB g schneidet und die BC nicht geschnitten wird dann muss wegen des Satz von Patsch g die Streche AC schneiden!knechtk
die punkte sollen in diesem fall kollinear sein, also auf einer "linie" liegen.
- damit ist es nicht der Satz von Pasch, aber diesen könnte man sicher für den Beweis verwenden!--Tutorin Anne 15:48, 6. Jun. 2012 (CEST)
Wer versucht's mal selber? z.B. Tabelarisch:--Tutorin Anne 15:53, 6. Jun. 2012 (CEST)
| Voraussetzung | (V. hier eintragen) |
| Behauptung | (Beh. hier eintragen) |
| Beweisschritt | Begründung |
|---|---|
| 1 (Schritt 1) | (Begründung 1) |
| 2 (Schritt 2) | (Begründung 2) |
| 3 (Schritt) | (Begründung) |
| 4 (Schritt) | (Begründung) |
Hier unten kommt gleich eine Lösung von Studentin.--Tutorin Anne 15:53, 6. Jun. 2012 (CEST)
wir haben also eine ebene e, in der eine gerade g liegt.
außerdem liegt in der ebene e die punkte a, b, c, diese dürfen nicht auf der geraden g liegen.
voraussetzung: 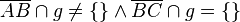
behauptung: 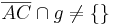
ich nehme mir nur den punkt a, um die ebene in zwei halbebenen ga+ und ga- zu teilen.
laut voraussetzung schneidet die strecke ab die gerade g, daher muss b auf ga- liegen (laut unserer def. der halbebenen)
da die strecke bc die gerade g nicht schneidet (siehe voraussetzung), liegt c (wie ebenso b) auf der halbebenen ga-.
daher muss die strecke ac die gerade g schneiden: denn a liegt auf ga+ und c auf ga-
reicht das so?
Ja, so kann man es beweisen!--Tutorin Anne 15:53, 6. Jun. 2012 (CEST)
--Studentin 16:35, 3. Jun. 2012 (CEST)