Winkel SS 2012: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Die Idee des gerichteten Winkels) |
*m.g.* (Diskussion | Beiträge) (→Beweis von Satz V.1) |
||
| Zeile 43: | Zeile 43: | ||
:: Das Innere eines Winkels ist konvex. | :: Das Innere eines Winkels ist konvex. | ||
==== Beweis von Satz V.1 ==== | ==== Beweis von Satz V.1 ==== | ||
| − | ::trivial entsprechend Satz IV., Satz IV.3 und der Definition V.2 | + | ::trivial entsprechend Satz IV.2, Satz IV.3 und der Definition V.2 |
=== Nullwinkel, gestreckte Winkel, überstumpfe Winkel? === | === Nullwinkel, gestreckte Winkel, überstumpfe Winkel? === | ||
Version vom 9. Juni 2012, 07:16 Uhr
|
Definition des WinkelbegriffsDefinition V.1: (Winkel)
Arten, Winkel zu beschreiben bzw. zu bezeichnenZur Bezeichnung von Winkeln werden üblicherweise kleine griechische Buchstaben verwendet. Über Punkte und Halbgeraden kann man Winkel wie folgt bezeichnen:
Das Innere eines WinkelsSo ist es zu verstehen[ www.ph-heidelberg.de is not an authorized iframe site ] Definition des Inneren eines WinkelsDefinition V.2: (Inneres eines Winkels)
Satz V.1
Beweis von Satz V.1
Nullwinkel, gestreckte Winkel, überstumpfe Winkel?Bemerkung: Entsprechend Definition V.2 beinhaltet unsere Geometrie keine überstumpfen Winkel, keinen Nullwinkel und keine gestreckten Winkel. Scheitelwinkel und NebenwinkelScheitelwinkelBeispiele und GegenbeispieleSie werden den Begriff des Scheitelwinkels mit Ihren Schülern erarbeiten müssen. Entwickeln Sie ein Arbeitsblatt, das Repräsentanten und Gegenrepräsentanten bezüglich des Begriffs Scheitelwinkel enthält und binden Sie dieses in die folgende Datei ein: DefinitionDefinition V.3: (Scheitelwinkel)
NebenwinkelBeispiele und GegenbeispieleSie werden den Begriff des Nebenwinkels mit Ihren Schülern erarbeiten müssen. Entwickeln Sie ein Arbeitsblatt, das Repräsentanten und Gegenrepräsentanten bezüglich des Begriffs Scheitelwinkel enthält und binden Sie dieses in die folgende Datei ein: DefinitionDefinition V.4: (Nebenwinkel)
|
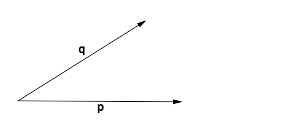
 und
und  besteht.
besteht.
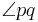
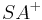 und
und 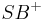 besteht.
besteht.

 ist ...
ist ...

