Lösung von Aufgabe 7.3 S (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 2: | Zeile 2: | ||
<u>Satz:</u> Sind zwei Punktmengen konvex, dann ist auch ihr Durchschnitt konvex.<br/> | <u>Satz:</u> Sind zwei Punktmengen konvex, dann ist auch ihr Durchschnitt konvex.<br/> | ||
| + | <u>Beweis:</u>? | ||
<u>Kontraposition:</u> Ist der Durchschnitt zweier Punktmengen nicht konvex, so sind die beiden Punktmengen auch nicht konvex. <br/> | <u>Kontraposition:</u> Ist der Durchschnitt zweier Punktmengen nicht konvex, so sind die beiden Punktmengen auch nicht konvex. <br/> | ||
<u>Umkehrung des Satzes:</u> Ist der Durchschnitt zweier Punktmengen konvex, dann sind die beiden Punktmengen konvex. | <u>Umkehrung des Satzes:</u> Ist der Durchschnitt zweier Punktmengen konvex, dann sind die beiden Punktmengen konvex. | ||
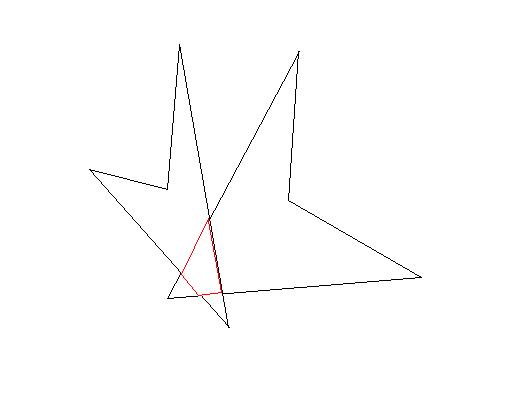
<u>Widerlegung der Umkehrung durch eine Skizze:</u> [[Datei:RitterSport_Konvex.JPG]] | <u>Widerlegung der Umkehrung durch eine Skizze:</u> [[Datei:RitterSport_Konvex.JPG]] | ||
--[[Benutzer:RitterSport|RitterSport]] 19:52, 9. Jun. 2012 (CEST) | --[[Benutzer:RitterSport|RitterSport]] 19:52, 9. Jun. 2012 (CEST) | ||
Version vom 9. Juni 2012, 19:18 Uhr
Lösungsvorschlag:
Satz: Sind zwei Punktmengen konvex, dann ist auch ihr Durchschnitt konvex.
Beweis:?
Kontraposition: Ist der Durchschnitt zweier Punktmengen nicht konvex, so sind die beiden Punktmengen auch nicht konvex.
Umkehrung des Satzes: Ist der Durchschnitt zweier Punktmengen konvex, dann sind die beiden Punktmengen konvex.
Widerlegung der Umkehrung durch eine Skizze: 
--RitterSport 19:52, 9. Jun. 2012 (CEST)
