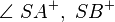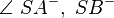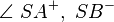Winkel SS 2012: Unterschied zwischen den Versionen
(→Definition V.4: (Nebenwinkel)) |
(→Definition V.4: (Nebenwinkel)) |
||
| Zeile 102: | Zeile 102: | ||
::Zwei Winkel bilden ein Paar von Nebenwinkeln, wenn sie supplementär sind/sich zu 180 Grad ergänzen.<br /> | ::Zwei Winkel bilden ein Paar von Nebenwinkeln, wenn sie supplementär sind/sich zu 180 Grad ergänzen.<br /> | ||
--[[Benutzer:*osterhase*|*osterhase*]] 19:29, 10. Jun. 2012 (CEST)<br /> | --[[Benutzer:*osterhase*|*osterhase*]] 19:29, 10. Jun. 2012 (CEST)<br /> | ||
| − | '''Definitionsversuch Nebenwinkel von Nummero6/Tchu Tcha Tcha:'''<br /> | + | '''Definitionsversuch 1 - Nebenwinkel von Nummero6/Tchu Tcha Tcha:'''<br /> |
::Zwei Winkel bilden ein Paar von Nebenwinkeln, wenn beide Scheitelpunkte identisch sind, jeweils genau ein Schenkel identisch ist | ::Zwei Winkel bilden ein Paar von Nebenwinkeln, wenn beide Scheitelpunkte identisch sind, jeweils genau ein Schenkel identisch ist | ||
| − | ::und | + | ::und die beiden anderen Schenkel jeweils Teilmenge von genau einer Geraden sind.<br /> |
| + | '''Definitionsversuch 2 - Nebenwinkel:'''<br /> | ||
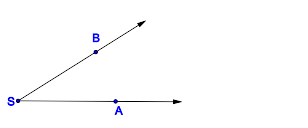
| + | ::Zwei Winkel bilden ein Paar von Scheitelwinkeln, wenn für die beiden Schenkel gilt:<br /> | ||
| + | ::Winkel 1: <math>\angle \ SA^{+} ,\ SB^{+}</math><br /> | ||
| + | ::Winkel 2: <math>\angle \ SA^{+} ,\ SB^{-}</math><br /> | ||
| + | |||
--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 21:04, 10. Jun. 2012 (CEST) | --[[Benutzer:Nummero6|Tchu Tcha Tcha]] 21:04, 10. Jun. 2012 (CEST) | ||
Version vom 10. Juni 2012, 20:12 Uhr
|
Definition des WinkelbegriffsDefinition V.1: (Winkel)
Arten, Winkel zu beschreiben bzw. zu bezeichnenZur Bezeichnung von Winkeln werden üblicherweise kleine griechische Buchstaben verwendet. Über Punkte und Halbgeraden kann man Winkel wie folgt bezeichnen:
Das Innere eines WinkelsSo ist es zu verstehen[ www.ph-heidelberg.de is not an authorized iframe site ] Definition des Inneren eines WinkelsDefinition V.2: (Inneres eines Winkels)
Satz V.1
Beweis von Satz V.1
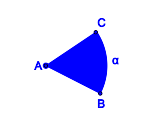
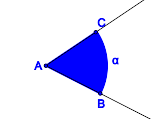
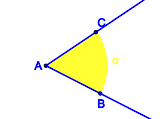
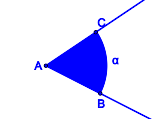
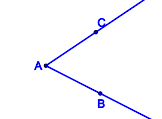
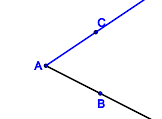
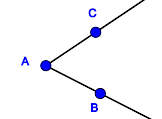
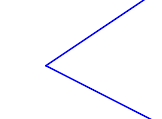
Nullwinkel, gestreckte Winkel, überstumpfe Winkel?Entsprechend Definitionen V.1 und V.2 beinhaltet unsere Geometrie keine überstumpfen Winkel, keinen Nullwinkel und keine gestreckten Winkel. Bis hierhin alles verstanden?In welchen Fällen sind die jeweils blau gefärbten Punktmengen Modelle für Winkel?
Bemerkung: Halbgeraden können natürlich nicht vollständig gezeichnet werden. Die Zeichnungen sind so zu verstehen, dass die Schenkel Halbgeraden sind. Videos zum WinkelbegriffScheitelwinkel und NebenwinkelScheitelwinkelBeispiele und GegenbeispieleSie werden den Begriff des Scheitelwinkels mit Ihren Schülern erarbeiten müssen. Entwickeln Sie ein Arbeitsblatt, das Repräsentanten und Gegenrepräsentanten bezüglich des Begriffs Scheitelwinkel enthält und binden Sie dieses in die folgende Datei ein: DefinitionDefinition V.3: (Scheitelwinkel)
Definitionsversuch 2 Scheitelwinkel:
--Tchu Tcha Tcha 20:47, 10. Jun. 2012 (CEST) NebenwinkelBeispiele und GegenbeispieleSie werden den Begriff des Nebenwinkels mit Ihren Schülern erarbeiten müssen. Entwickeln Sie ein Arbeitsblatt, das Repräsentanten und Gegenrepräsentanten bezüglich des Begriffs Scheitelwinkel enthält und binden Sie dieses in die folgende Datei ein: DefinitionDefinition V.4: (Nebenwinkel)
--*osterhase* 19:29, 10. Jun. 2012 (CEST)
Definitionsversuch 2 - Nebenwinkel:
--Tchu Tcha Tcha 21:04, 10. Jun. 2012 (CEST)
|
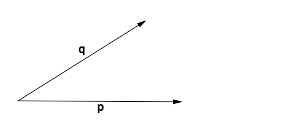
 und
und 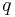 besteht.
besteht.
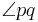
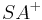 und
und 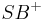 besteht.
besteht.

 ist ...
ist ...