Lösung von Zusatzaufgabe 3.4 (SoSe 12): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „== Aufgabe 4== Beweisen Sie die Äquvalenzaussage '''Für alle n <math>\epsilon</math> <math>\mathbb{N}</math> gilt: n ist gerade <math>\Leftrightarrow</math> n…“)
 
K (→‎Anmerkungen von Buchner zur Lösung von Tchu Tcha Tcha)
 
(6 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 2: Zeile 2:
 
Beweisen Sie die Äquvalenzaussage
 
Beweisen Sie die Äquvalenzaussage
 
'''Für alle n  <math>\epsilon</math> <math>\mathbb{N}</math> gilt: n ist gerade <math>\Leftrightarrow</math> n<sup>2</sup> ist gerade.'''<br />
 
'''Für alle n  <math>\epsilon</math> <math>\mathbb{N}</math> gilt: n ist gerade <math>\Leftrightarrow</math> n<sup>2</sup> ist gerade.'''<br />
 +
<br />
 +
<u>Implikation:</u> Wenn <math>n\in N</math> gerade ist, dann ist auch <math>n^{2}</math> gerade.<br />
 +
<u>Umkehrung:</u> Wenn <math>n^{2}</math> gerade ist, dann ist auch <math>n\in N</math> gerade.
  
 +
'''Beweis Implikation:'''<br />
 +
Voraussetzung: <math>n\in N</math> gerade<br />
 +
Behauptung:<math>n^{2}</math> gerade<br />
 +
Annahme: <math>n^{2}</math> ungerade
 +
 +
(1) <math>n\in N</math> gerade / Vor.<br />
 +
(2) <math>n^{2}</math> kann nur ungerade sein, wenn man zwei ungerade Zahlen miteinander multipliziert. / trivial, Widerspruch zur Vor.<br />
 +
(3) Annahme zu verwerfen. / (2)<br />
 +
(4) Behauptung stimmt / (3)<br />
 +
q.e.d.<br /><br />
 +
 +
'''Beweis Umkehrung:'''<br />
 +
Voraussetzung: <math>n^{2}</math> gerade<br />
 +
Behauptung: <math>n\in N</math> gerade<br />
 +
Annahme: <math>n\in N</math> ungerade
 +
 +
(1) <math>n^{2}</math> gerade / Vor.<br />
 +
(2) <math>n\in N</math> kann nur gerade sein, wenn die Quadratwurzel (nach Vor.) gerade ist. / trivial, Widerspruch zur Vor.<br />
 +
(3) Annahme zu verwerfen. / (2)<br />
 +
(4) Behauptung stimmt / (3)<br />
 +
q.e.d.<br />
 +
--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 10:30, 8. Jun. 2012 (CEST)
 +
 +
== Anmerkungen von Buchner zur Lösung von Tchu Tcha Tcha ==
 +
Ihre Herangehensweise ist absolut korrekt, Voraussetzungen und Behauptungen stimmen jeweils. Man beweist Ihren jeweils zweiten Schritt in der Regel genauer, d.h. das was Sie als trivial bezeichnet haben führt man aus.<br /><br />
 +
'''Beweis der Umkehrung'''<br />
 +
Voraussetzung: <math>n^{2}</math> gerade<br />
 +
Behauptung: <math>n\in N</math> gerade<br />
 +
Annahme: <math>n\in N</math> ungerade<br />
 +
 +
(1) <math>n\in N</math> ungerade, d.h. <math>\exists m\in N: n = 2m +1 </math>  /nach Ann. (so schreibt man formal, dass eine Zahl ungerade ist- zu jeder ungeraden Zahl (n) gibt es irgendeine natürliche Zahl (m), die man verdoppelt und dann plus eins rechnet, sodass man n erhält (2m gerade, durch plus eins wirds ungerade)<br />
 +
(2) n = 2m +1, dann ist <math>n^{2} = (2m +1)^{2}= 4m^{2}+ 4m + 1</math> / (1), Rechnen in R <br />
 +
(3) Wegen <math>4m^{2}</math> und <math>4m</math> ist gerade ist <math>4m^{2}+ 4m + 1</math> ungerade. / Begründung z.B. Teilbarkeitsregeln oder auch 2 ausklammern [ <math>2*(2m^{2}+ 2m) + 1</math> ] und Schritt (2)<br />
 +
'''Widerspruch''' zur Vor.<br />
 +
Behauptung stimmt.<br /><br />
 +
 +
Entsprechend würde man die '''Hinrichtung''' beweisen - am einfachsten durch einen '''direkten Beweis''', dann gehen Sie von n gerade aus, d.h. Sie sagen:<br />
 +
<math>\exists m\in N: n = 2m </math>. <br />
 +
Können Sie weitermachen?<br />
 +
 +
--[[Benutzer:Buchner|Buchner]] 10:53, 11. Jun. 2012 (CEST)
 +
 +
'''Lösungsversuch 2 von Nummero6/Tchu Tcha Tcha:'''<br />
 +
'''Beweis Hinrichtung (Implikation):'''<br />
 +
Voraussetzung: <math>n\in N</math> gerade<br />
 +
Behauptung:<math>n^{2}</math> gerade<br />
 +
'''Direkter Beweis'''<br />
 +
(1) <math>n\in N</math> gerade, d.h. <math>\exists m\in N: n = 2m </math>  / nach Voraussetzung <br />
 +
(2) n = 2m, dann ist <math>n^{2} = (2m)^{2}= 4m^{2}</math> / (1), Rechnen in R <br />
 +
(3) <math>4m^{2}</math> gerade / Begründung Teilbarkeitsregeln <br />
 +
(4) Wegen <math>4m^{2}=n^{2}</math> ist <math>n^{2}</math> auch gerade / (2), (3) <br />
 +
(5) Behauptung stimmt / (4) <br />
 +
q.e.d.<br />
 +
--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 20:46, 11. Jun. 2012 (CEST)
 +
<br /><br />
 +
Ganz genau! Super.<br />
 +
--[[Benutzer:Buchner|Buchner]] 10:48, 12. Jun. 2012 (CEST)<br />
 +
Danke :-)--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 11:10, 12. Jun. 2012 (CEST)
 
[[Kategorie: Einführung_S]]
 
[[Kategorie: Einführung_S]]

Aktuelle Version vom 12. Juni 2012, 12:39 Uhr

Aufgabe 4

Beweisen Sie die Äquvalenzaussage Für alle n \epsilon \mathbb{N} gilt: n ist gerade \Leftrightarrow n2 ist gerade.

Implikation: Wenn n\in N gerade ist, dann ist auch n^{2} gerade.
Umkehrung: Wenn n^{2} gerade ist, dann ist auch n\in N gerade.

Beweis Implikation:
Voraussetzung: n\in N gerade
Behauptung:n^{2} gerade
Annahme: n^{2} ungerade

(1) n\in N gerade / Vor.
(2) n^{2} kann nur ungerade sein, wenn man zwei ungerade Zahlen miteinander multipliziert. / trivial, Widerspruch zur Vor.
(3) Annahme zu verwerfen. / (2)
(4) Behauptung stimmt / (3)
q.e.d.

Beweis Umkehrung:
Voraussetzung: n^{2} gerade
Behauptung: n\in N gerade
Annahme: n\in N ungerade

(1) n^{2} gerade / Vor.
(2) n\in N kann nur gerade sein, wenn die Quadratwurzel (nach Vor.) gerade ist. / trivial, Widerspruch zur Vor.
(3) Annahme zu verwerfen. / (2)
(4) Behauptung stimmt / (3)
q.e.d.
--Tchu Tcha Tcha 10:30, 8. Jun. 2012 (CEST)

Anmerkungen von Buchner zur Lösung von Tchu Tcha Tcha

Ihre Herangehensweise ist absolut korrekt, Voraussetzungen und Behauptungen stimmen jeweils. Man beweist Ihren jeweils zweiten Schritt in der Regel genauer, d.h. das was Sie als trivial bezeichnet haben führt man aus.

Beweis der Umkehrung
Voraussetzung: n^{2} gerade
Behauptung: n\in N gerade
Annahme: n\in N ungerade

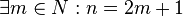(1) n\in N ungerade, d.h. \exists m\in N: n = 2m +1 /nach Ann. (so schreibt man formal, dass eine Zahl ungerade ist- zu jeder ungeraden Zahl (n) gibt es irgendeine natürliche Zahl (m), die man verdoppelt und dann plus eins rechnet, sodass man n erhält (2m gerade, durch plus eins wirds ungerade)
(2) n = 2m +1, dann ist 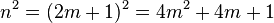n^{2} = (2m +1)^{2}= 4m^{2}+ 4m + 1 / (1), Rechnen in R
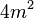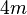(3) Wegen 4m^{2} und 4m ist gerade ist 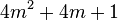4m^{2}+ 4m + 1 ungerade. / Begründung z.B. Teilbarkeitsregeln oder auch 2 ausklammern [ 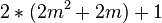2*(2m^{2}+ 2m) + 1 ] und Schritt (2)
Widerspruch zur Vor.
Behauptung stimmt.

Entsprechend würde man die Hinrichtung beweisen - am einfachsten durch einen direkten Beweis, dann gehen Sie von n gerade aus, d.h. Sie sagen:
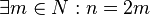\exists m\in N: n = 2m .
Können Sie weitermachen?

--Buchner 10:53, 11. Jun. 2012 (CEST)

Lösungsversuch 2 von Nummero6/Tchu Tcha Tcha:
Beweis Hinrichtung (Implikation):
Voraussetzung: n\in N gerade
Behauptung:n^{2} gerade
Direkter Beweis
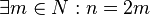(1) n\in N gerade, d.h. \exists m\in N: n = 2m / nach Voraussetzung
(2) n = 2m, dann ist 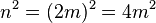n^{2} = (2m)^{2}= 4m^{2} / (1), Rechnen in R
(3) 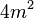4m^{2} gerade / Begründung Teilbarkeitsregeln
(4) Wegen 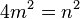4m^{2}=n^{2} ist n^{2} auch gerade / (2), (3)
(5) Behauptung stimmt / (4)
q.e.d.
--Tchu Tcha Tcha 20:46, 11. Jun. 2012 (CEST)

Ganz genau! Super.
--Buchner 10:48, 12. Jun. 2012 (CEST)
Danke :-)--Tchu Tcha Tcha 11:10, 12. Jun. 2012 (CEST)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Zusatzaufgabe_3.4_(SoSe_12)&oldid=14704“