Benutzer:*m.g.*: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Alles hat zwei Seiten oder grundlegende Ideen der Beschaffenheit von Ebenen) |
*m.g.* (Diskussion | Beiträge) (→Alles hat zwei Seiten oder grundlegende Ideen der Beschaffenheit von Ebenen) |
||
| Zeile 66: | Zeile 66: | ||
=== Definition des Begriffs der Halbebene === | === Definition des Begriffs der Halbebene === | ||
==== Alles hat zwei Seiten oder grundlegende Ideen der Beschaffenheit von Ebenen ==== | ==== Alles hat zwei Seiten oder grundlegende Ideen der Beschaffenheit von Ebenen ==== | ||
| − | |||
| − | |||
{| | {| | ||
|- | |- | ||
| Zeile 73: | Zeile 71: | ||
|[[Bild:Halbebene_00.png| 100 px]] | |[[Bild:Halbebene_00.png| 100 px]] | ||
|- | |- | ||
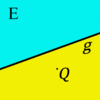
| − | | Zu der einen ''Hälfte'' von <math>\Epsilon</math> bezüglich <math>\ g</math> gehören alle die Punkte aus <math>\Epsilon \setminus g</math>, die mit <math>\ Q</math> auf derselben Seite von <math>\ g</math> liegen. Alle anderen Punkte aus <math>\Epsilon \setminus g</math> gehören zur anderen Seite von <math>\ \Epsilon</math> bezüglich <math>\ g</math>. | + | | Zu der einen ''Hälfte'' von <math>\ \Epsilon</math> bezüglich <math>\ g</math> gehören alle die Punkte aus <math>\Epsilon \setminus g</math>, die mit <math>\ Q</math> auf derselben Seite von <math>\ g</math> liegen. Alle anderen Punkte aus <math>\Epsilon \setminus g</math> gehören zur anderen Seite von <math>\ \Epsilon</math> bezüglich <math>\ g</math>. |
| [[Bild:Halbebene_01.png | 100 px]] | | [[Bild:Halbebene_01.png | 100 px]] | ||
|} | |} | ||
| + | ==== offene Halbebenen ==== | ||
| + | Die beiden Seiten, in die die Menge der Punkte einer Ebene <math>\ \Epsilon</math>, die nicht auf einer Geraden <math>\ g</math> dieser Ebene liegen, durch diese Gerade <math>\ g</math> eingeteilt werden, heißen offene Halbebenen von <math>\ \Epsilon</math> bezüglich der Trägergeraden <math>\ g</math>. Der nicht zu <math>\ g</math> gehörende Referenzpunkt <math>\ Q \in \Epsilon</math> bietet uns eine Möglichkeit zur Bezeichnung der beiden offenen Halbebenen. Die offene Halbebene, zu der alle Punkte gehören, die bezüglich <math>\ g</math> mit <math>\ Q</math> auf derselben seite liegen wird mit <math>gQ^{+}</math> bezeichnet, die andere offene Halbebene von <math>\ \Epsilon</math> bezüglich <math>\ g</math> und <math>\ Q</math> mit <math>gQ^{-}</math>. | ||
Version vom 3. Juni 2010, 08:28 Uhr
Inhaltsverzeichnis |
Halbebenen und das Axiom von Pasch
Halbebenen
Analogiebetrachtungen
| |
|
 , das in Klassen eingeteilt wird , das in Klassen eingeteilt wird | |
 ist eine ... ist eine ...
|
 ist eine ... ist eine ...
|
 | |
| Dimension von | Dimension von |
 , das , das  in Klassen einteilt in Klassen einteilt | |
 ist ... ist ...
|
 ist ... ist ...
|
 | |
 hat die Dimension ... hat die Dimension ...
|
 hat die Dimension ... hat die Dimension ...
|
 teilt teilt 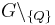 in genau zwei Klassen in genau zwei Klassen | |
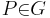 , die mit , die mit  bezüglich bezüglich  „auf derselben Seite liegen“ „auf derselben Seite liegen“ | |
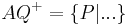
|
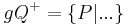
|
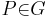 , die bezüglich , die bezüglich  nicht auf der Seite von nicht auf der Seite von  liegen. liegen. | |
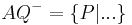
|
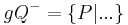
|
Definition des Begriffs der Halbebene
Alles hat zwei Seiten oder grundlegende Ideen der Beschaffenheit von Ebenen
offene Halbebenen
Die beiden Seiten, in die die Menge der Punkte einer Ebene  , die nicht auf einer Geraden
, die nicht auf einer Geraden  dieser Ebene liegen, durch diese Gerade
dieser Ebene liegen, durch diese Gerade  eingeteilt werden, heißen offene Halbebenen von
eingeteilt werden, heißen offene Halbebenen von  bezüglich der Trägergeraden
bezüglich der Trägergeraden  . Der nicht zu
. Der nicht zu  gehörende Referenzpunkt
gehörende Referenzpunkt 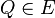 bietet uns eine Möglichkeit zur Bezeichnung der beiden offenen Halbebenen. Die offene Halbebene, zu der alle Punkte gehören, die bezüglich
bietet uns eine Möglichkeit zur Bezeichnung der beiden offenen Halbebenen. Die offene Halbebene, zu der alle Punkte gehören, die bezüglich  mit
mit  auf derselben seite liegen wird mit
auf derselben seite liegen wird mit 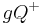 bezeichnet, die andere offene Halbebene von
bezeichnet, die andere offene Halbebene von  bezüglich
bezüglich  und
und  mit
mit 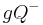 .
.
 gehört u.a., dass jede Gerade
gehört u.a., dass jede Gerade 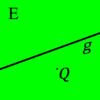
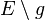 , die mit
, die mit