DefinitionsversucheV4: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) (→Variante 2) |
||
| Zeile 19: | Zeile 19: | ||
::Winkel 1: <math>\angle \ SA^{+} ,\ SB^{+}</math><br /> | ::Winkel 1: <math>\angle \ SA^{+} ,\ SB^{+}</math><br /> | ||
::Winkel 2: <math>\angle \ SA^{+} ,\ SB^{-}</math><br />}} | ::Winkel 2: <math>\angle \ SA^{+} ,\ SB^{-}</math><br />}} | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 21:04, 10. Jun. 2012 (CEST) | --[[Benutzer:Nummero6|Tchu Tcha Tcha]] 21:04, 10. Jun. 2012 (CEST) | ||
Version vom 13. Juni 2012, 17:07 Uhr
Inhaltsverzeichnis |
Die Vorgabe
Definition
V.4 (Nebenwinkel)
Zwei Winkel bilden ein Paar von Nebenwinkeln,
Definition von osterhase
Definition
V.4 (Nebenwinkel)
Zwei Winkel bilden ein Paar von Nebenwinkeln, wenn sie supplementär sind/sich zu 180 Grad ergänzen.
--*osterhase* 19:29, 10. Jun. 2012 (CEST)
Definition von Nummero6/TchuTcha Tcha
Variante 1
Definition
V.4 (Nebenwinkel)
Zwei Winkel bilden ein Paar von Nebenwinkeln, wenn beide Scheitelpunkte identisch sind, jeweils genau ein Schenkel identisch ist und die beiden anderen Schenkel jeweils Teilmenge von genau einer Geraden sind.
Definitionsversuch 1 - Nebenwinkel von Nummero6/Tchu Tcha Tcha:
- Zwei Winkel bilden ein Paar von Nebenwinkeln, wenn beide Scheitelpunkte identisch sind, jeweils genau ein Schenkel identisch ist
- und die beiden anderen Schenkel jeweils Teilmenge von genau einer Geraden sind.
Variante 2
Definition
V.4 (Nebenwinkel)
Zwei Winkel bilden ein Paar von Nebenwinkeln, wenn für die beiden Schenkel gilt:
- Winkel 1:
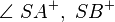
- Winkel 2:
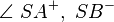
- Winkel 1:
--Tchu Tcha Tcha 21:04, 10. Jun. 2012 (CEST)

