Lösung von Aufgabe 7.3 S (SoSe 12): Unterschied zwischen den Versionen
Nemo81 (Diskussion | Beiträge) |
Nemo81 (Diskussion | Beiträge) |
||
| Zeile 16: | Zeile 16: | ||
| − | + | Beh: Ihr schnitt ist Konvex M1 geschnitten M2 = konvex bedeutet: Strecke AB ist echte Teilmenge von M1 und M2 | |
Ann: Es existiert ein Punkt P: P ist element der Strecke AB und P ist nicht element M2. | Ann: Es existiert ein Punkt P: P ist element der Strecke AB und P ist nicht element M2. | ||
| − | Es kann solch einen Punkt nicht geben, weil laut Vor: Die Strecke AB echte teilmenge von M1 aber auch von M2 ist( und laut def Konvex) | + | Es kann solch einen Punkt nicht geben, weil laut Vor: Die Strecke AB echte teilmenge von M1 aber auch von M2 ist(und laut def Konvex) |
Also Widerspruch zur Vorraussetzung. q.e.d --[[Benutzer:Nemo81|Nemo81]] 17:57, 14. Jun. 2012 (CEST) | Also Widerspruch zur Vorraussetzung. q.e.d --[[Benutzer:Nemo81|Nemo81]] 17:57, 14. Jun. 2012 (CEST) | ||
Version vom 14. Juni 2012, 18:06 Uhr
Lösungsvorschlag:
Satz: Sind zwei Punktmengen konvex, dann ist auch ihr Durchschnitt konvex.
Beweis: ?
Kontraposition: Ist der Durchschnitt zweier Punktmengen nicht konvex, so sind die beiden Punktmengen auch nicht konvex.
Umkehrung des Satzes: Ist der Durchschnitt zweier Punktmengen konvex, dann sind die beiden Punktmengen konvex.
Widerlegung der Umkehrung durch eine Skizze: 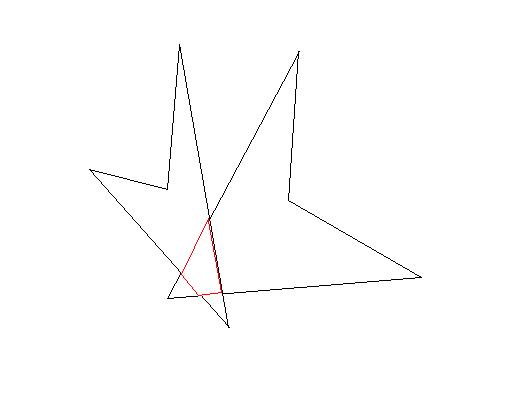
 --KeinKurpfälzer 16:25, 11. Jun. 2012 (CEST)
--KeinKurpfälzer 16:25, 11. Jun. 2012 (CEST)
 --KeinKurpfälzer 17:35, 11. Jun. 2012 (CEST)
--KeinKurpfälzer 17:35, 11. Jun. 2012 (CEST)
Vor: 2 konvexe Punktmengen 1. Strecke AB ist echte Teilmenge von Menge1 (M1) 2. Strecke AB ist echte Teilmenge von M2
Beh: Ihr schnitt ist Konvex M1 geschnitten M2 = konvex bedeutet: Strecke AB ist echte Teilmenge von M1 und M2
Ann: Es existiert ein Punkt P: P ist element der Strecke AB und P ist nicht element M2.
Es kann solch einen Punkt nicht geben, weil laut Vor: Die Strecke AB echte teilmenge von M1 aber auch von M2 ist(und laut def Konvex) Also Widerspruch zur Vorraussetzung. q.e.d --Nemo81 17:57, 14. Jun. 2012 (CEST)

