Verkettung zweier Geradenspiegelungen SoSe 12: Unterschied zwischen den Versionen

Version vom 21. Juni 2012, 09:11 Uhr

Inhaltsverzeichnis

1 Verkettung von Abbildungen
- 1.1 Definition IX.1 : (Verkettung von Abbildungen)
- 1.2 Verkettung zweier Geradenspiegelungen

Verkettung von Abbildungen

Definition IX.1 : (Verkettung von Abbildungen)

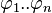Unter einer Verkettung von Abbildungen versteht man das Hintereinanderausführen zweier oder mehrerer Abbildungen $\varphi _{1}..\varphi _{n}$ .
Schreibweise: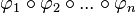 $\varphi _{1}\circ\varphi _{2}\circ ... \circ \varphi _{n}$ .

Anmerkung: In der Literatur wird die Reihenfolge der Verkettung unterschiedlich angewendet: 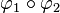$\varphi _{1}\circ\varphi _{2}$ kann bedeuten, dass man zuerst 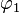$\varphi _{1}$ und dann 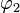$\varphi _{2}$ ausführen muss, aber auch die umgekehrte Reihenfolge wird verwendet. Wir einigen uns im Rahmen dieser Veranstaltung für die erste Variante, also die Ausführungsreihenfolge von links nach rechts.

Verkettung zweier Geradenspiegelungen

Gegeben seien zwei Geraden a und b. Wir betrachten die Verkettung $S_{a}\circ S_{b}$ .
Aufgabe: Welche prinzipiellen Möglichkeiten bezüglich der Lage der beiden Geraden a und b gibt es? Ihre Antwort:

Wir betrachten zunächst zwei sich schneidende Spiegelgeraden: Experimentieren Sie mit dem nachfolgenden Applet, indem Sie die Verkettung der beiden Geradenspiegelungen ausführen, d. h. auf das Dreieck anwenden. Welche Zusammenhänge entdecken Sie?

Satz IX.1 :

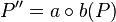Gegeben seien zwei Spiegelgeraden a und b mit einem gemeinsamen Schnittpunkt S. Wir betrachten die Verkettung $S_{a}\circ S_{b}$ . Jeder Punkt P liegt dabei mit seinem Bildpunkt $P''=a\circ b(P)$ auf einem Kreis k um S.
Beweis:

Satz IX.2 :

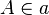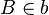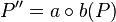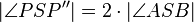Gegeben seien zwei Spiegelgeraden a und b mit einem gemeinsamen Schnittpunkt S, sowie zwei Punkten $A\in a$ und $B\in b$ , die von S jeweils verschieden sind. Wir betrachten die Verkettung $S_{a}\circ S_{b}$ . Für einen beliebigen Punkt P und seinen Bildpunkt $P''=a\circ b(P)$ gilt: $\left| \angle PSP'' \right| =2\cdot\left| \angle ASB \right|$ .
Beweis:

Eine Abbildung, wie wir sie auf dieser Seite kennengelernt haben, nennen wir auch Drehung. Definieren Sie im Folgenden den Begriff Drehung:

Definition IX.2 (Drehung):

Eine Drehung ist ... (Ergänzen Sie)

@@ Zeile 10: / Zeile 10: @@
 <ggb_applet width="649" height="538"  version="4.0" ggbBase64="UEsDBBQACAAIANCD0kAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIANCD0kAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vltb9s2EP7c/gpCnxuZpKgXF06Ltlu3AOkLkG4Y9mWgJdpmI4uaSDt20R+/IynJUtKXBE26pkETvh15vOeeO57d2dPdukRb0WipquOAhDhAospVIavlcbAxi6MsePrk4Wwp1FLMG44WqllzcxwwKymL42DBKRXpAh8VCY2PmEjTo2mWF0eLnCyyYo4zHPMAoZ2Wjyv1mq+FrnkuzvKVWPNTlXPjFK+MqR9PJhcXF2GnKlTNcrJczsOdLgIE16z0cdB2HsNxo00XkROnGJPJX69O/fFHstKGV7kIkDVhI588fDC7kFWhLtCFLMzqOEjiNEArIZcrsCnBYNPECtUASC1yI7dCw9bB0Nls1nXgxHhl1x/4Hip7cwJUyK0sRHMc4DDCjBGGsW8DpBopKtNKklbjpDtrtpXiwh9qe04fbDJKlXNuz0MfPyKKKUaPbEN8Q6FJEr+E/RyOfEN9w3wTexnmtzMvyrwM8zIsCtBWajkvhXVvqQE/WS0a8F0/1mZfCnefduJgO3kENmn5AYQjC6gHHOYxfmR/AeVHrEN6YCQZaDXN5oZKO5UJm15fJf0mQ6NOJ/2UmTT+jJnJF5R6u69jJ4kHOkGV++d+r2iMvmTmZY1+/G0KE/ZdTJxNulCZtdGB9MrKtuwxYq1tvERTFE8t7QmKITaSFFgeIzKFJqUIogGRGLEYhiRDiW1TFKWwwFCEMmTlSIRccMQZ/GGpOyxBMRxmZ1OISURAEUNxhIiLKYYgkpCLS4hRGoFEHKMYNln1hNojogSxBEZRhhjc0YZkSkAwgo0wBvUURQRFdjNJEU1QYs8jzIZ6ktmrw5EUJRglxB4IUQ0R7aMZ5DMUWWuSFi5Z1RszgihfF13XqLr3BUhDPjrkPJ+fRinxwazkc1HCK3FmPYnQlpc2IpyihaoM6pxI/dyy4fVK5vpMGAO7NHrPt/yUG7F7CdK60+1kc1Xpt40yL1S5WVcaoVyVuL+zKsmgT/tbwyAaLLDhQjxYSAb99JN6FaygjRagXzW6E+dFcWIlDqkBkHxTlfvnjeDntZJjM2YT9+DMxCYvZSF59SeQ1WqxuKD+/bHpqnt/WJR2F1FNcbbXwGC0+1s0ygbDNJwOf+Dd2vuliCb2MdY5t/HGLsll4P59uxZjEHQaxLZ3BN+Jg03LRvaUsP0T/VyVRb/srHzBa7NpXIEAKbCxd39WLUvhmOCSKry++flc7c48BSJ/1rt9DaP2AvOlQxdBBqBxDAJtO/etk7E366Wwk8FOAneckkW/TqbUSbh27lsnBST1V2stJZ2VBHdqpHZ5CwdtdHQ5yVLcPuabSprTbmBkft6aSvyG15v1XPREGZ9JbuvM2eQSk2bnoqlE2RIXfLlRG+3jcMDpQuRyDUO/0ELCrbv+gAv42UIsG9FdvHTFlwfMreIhJ69Mu6NeNmp9Um3fARcuXWA26W4503kja0s5NIdkfy4OrCqk5vBWFMN9NtLA9Ny+CQCPsdBADG7MSjWuvoLUAa0NsFKsoZ5CxtHLMbSH+cyVaRZPpObvIXv1D5xfPzgMlj9JNUdKXtYrbku51uiS70UzgsGd90oVY3AWcicKP3PQ5IDUaAdnhxm8lHvbYRClH3z97QtQa4YNn1Fi9bOXfADE8Ah8BYvnV7EYc/KOweAVENG5E/Ja7YleC+FjxF8YOjUc51LLKC93iJEwc4CxkNI7B+zFTwAYUIw6xKIwuXuKPft/w+02ADvCDqi9VU+zO0fsl/uPGAmJD0oSsrsH7Nf7DxgOpx4w4NrtZLFcrde8KlDlPmG9VeV+qargUPNzbGMTcWIJhzi1MHqMNqZbh6KihKqNeDHhxfg/dgxldeFVtoo+4SOvsvNCf9i4ADPwCeC8Elq7KtG09aDr/C6LQrhPf5MvO3gA6dDDJI6cj2PSVogHF5ObuPjzPNRiaUf9RcRXmHjzi96Qi4OkRULahmAWjar/qeMXrEc4vVIPX98d4t/Kb9G+SJXrupS5ND2LSsv3k8pAySpczXa1Ej0XorYfAd5U7xpeaftF4rg0uj70lpY/DPgkTPpwJmPwp0kHf5Il7KeBv/hxwAfMWYZHP76ktpiz0TxxvgAfMTpaiO6tX8Yv48v7/zIyV3KB9+LbKiXGL+Mp+PjSs3jm37uXV95D/uUXz9LlkI++GfrbCYYoxHTE+bgrzMahwBy2cYgjdkdZ6bqk/e3+kxbq36T9UJp+X9L+doW08xuQdv6DkJaG0Zi0UZ/AWzhxmFLA+M6JOhl+6eS+wW3/K/LJf1BLBwgc1dxupgYAACcdAABQSwECFAAUAAgACADQg9JA1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIANCD0kAc1dxupgYAACcdAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAPQcAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" /><br /><br />
-===== Sastz IX.1 :  =====
+===== Satz IX.1 :  =====
 Gegeben seien zwei Spiegelgeraden ''a'' und ''b'' mit einem gemeinsamen Schnittpunkt ''S''. Wir betrachten die Verkettung <math>S_{a}\circ S_{b} </math>. Jeder Punkt ''P'' liegt dabei mit seinem Bildpunkt <math>P''=a\circ b(P) </math> auf einem Kreis ''k'' um ''S''.<br />
 '''Beweis:'''<br /><br />

Verkettung zweier Geradenspiegelungen SoSe 12: Unterschied zwischen den Versionen

Version vom 21. Juni 2012, 09:11 Uhr

Inhaltsverzeichnis

Verkettung von Abbildungen

Definition IX.1 : (Verkettung von Abbildungen)

Verkettung zweier Geradenspiegelungen

Satz IX.1 :

Satz IX.2 :

Definition IX.2 (Drehung):

Navigationsmenü

Meine Werkzeuge

Namensräume

Varianten

Ansichten

Aktionen

Suche

Navigation

Werkzeuge