Benutzer:Tutorin Anne: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Funktionen (Elementare Funktionen)) |
(→Tabelle als Vorlage) |
||
| Zeile 13: | Zeile 13: | ||
| + | {| class="wikitable" | ||
| + | | Voraussetzung || (V. hier eintragen) | ||
| + | |- | ||
| + | | Behauptung || (Beh. hier eintragen) | ||
| + | |} | ||
| + | <br /> | ||
| + | |||
| + | {| class="wikitable" | ||
| + | !Beweisschritt!!Begründung | ||
| + | |- | ||
| + | | 1 (Schritt 1 hier)|| (Begründung 1) | ||
| + | |- | ||
| + | | 2 (Schritt 2) || (Begründung 2) | ||
| + | |- | ||
| + | | 3 (Schritt) || (Begründung) | ||
| + | |- | ||
| + | | 4 (Schritt) || (Begründung) | ||
| + | |} | ||
| + | <br /> | ||
| + | =SS12, Übung 10.3 Umkehrung des Basiswinkelsatzes, direkter Beweis= | ||
{| class="wikitable" | {| class="wikitable" | ||
| Voraussetzung || (V. hier eintragen) | | Voraussetzung || (V. hier eintragen) | ||
Version vom 3. Juli 2012, 21:38 Uhr
Inhaltsverzeichnis |
Mandala ganz einfach selbst gemacht!
Wo sich überall Mathematik verbirgt?!
Die Idee kam so
Tabelle als Vorlage
| Voraussetzung | (V. hier eintragen) |
| Behauptung | (Beh. hier eintragen) |
| Beweisschritt | Begründung |
|---|---|
| 1 (Schritt 1 hier) | (Begründung 1) |
| 2 (Schritt 2) | (Begründung 2) |
| 3 (Schritt) | (Begründung) |
| 4 (Schritt) | (Begründung) |
SS12, Übung 10.3 Umkehrung des Basiswinkelsatzes, direkter Beweis
| Voraussetzung | (V. hier eintragen) |
| Behauptung | (Beh. hier eintragen) |
| Beweisschritt | Begründung |
|---|---|
| 1 (Schritt 1 hier) | (Begründung 1) |
| 2 (Schritt 2) | (Begründung 2) |
| 3 (Schritt) | (Begründung) |
| 4 (Schritt) | (Begründung) |
Funktionen (Elementare Funktionen SS 11)
Quadratische Funktion und ihr Graph, eine Parabel
Tutorium SS11
Tutorium 13, Aufgabe 1
| Voraussetzung | 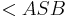 sei ein beliebiger Winkel sei ein beliebiger Winkel
|
| Behauptung | 1. Existenz einer Winkelhalbierenden 2. Eindeutigkeit dieser Wh |
Beweis zu 1.
z.z. Es exisitert ein Strahl 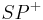 , für den gilt
, für den gilt 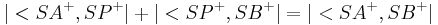 und
und 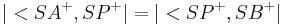 .
.
| 1) | 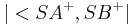 ist eine reele Zahl zwischen 0 und 180 ist eine reele Zahl zwischen 0 und 180 |
... |
| 2) | ... | ... |
| 3) | ... | ... |
| 4) | ... | ... |
| 5) | ... | ... |
Tutorium 3, Aufgabe 2

